人教版数学七年级上册1.2.4第1课时 绝对值课件(13张)
文档属性
| 名称 | 人教版数学七年级上册1.2.4第1课时 绝对值课件(13张) |  | |
| 格式 | ppt | ||
| 文件大小 | 860.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-30 11:39:56 | ||
图片预览





文档简介
第一章 有理数
1.2 有理数
1.2.4 绝对值
第1课时 绝对值
一、教学目标
1.理解绝对值的意义,使学生学会求一个数的绝对值.
2.通过观察、比较、归纳得出绝对值的概念,感受数形结合的思想.
重点
难点
理解绝对值的意义,会求一个数的绝对值.
对绝对值概念的理解.
二、教学重难点
活动1 新课导入
三、教学设计
1.10的相反数是 .
-10
答:-2的相反数是2;
2.-2,4, ,0,2 020的相反数分别是什么?
4的相反数是-4;
0的相反数是0;
2 020的相反数是-2 020.
的相反数是 ;
活动2 探究新知
1.教材P11 内容.
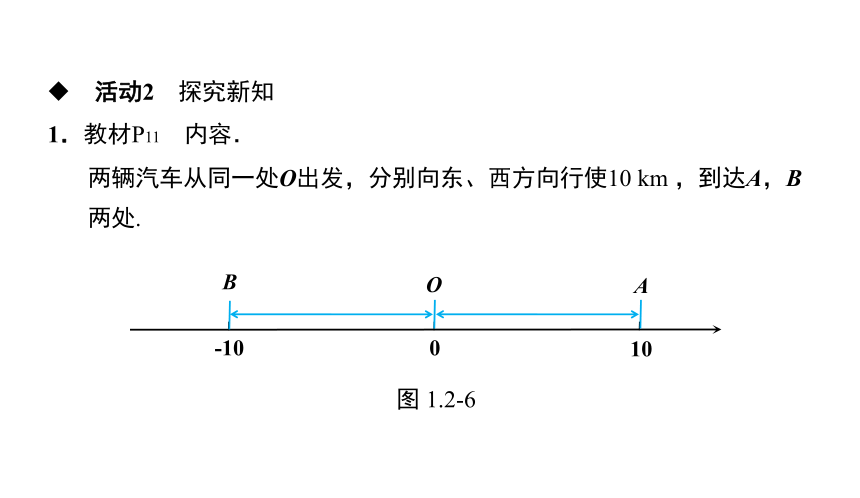
两辆汽车从同一处O出发,分别向东、西方向行使10 km ,到达A,B两处.
A
O
B
0
10
-10
图 1.2-6
活动2 探究新知
1.教材P11 内容.
提出问题:
思考完成并交流展示.
(2)甲、乙两辆汽车行驶的路程各是多少?它们行驶的路程相等吗?
(3)你还能列举出类似的例子吗?
(1)甲、乙两辆汽车的位置如何表示?它们的行驶路线相同吗?
活动2 探究新知
2.思考并回答下列问题:
(1)在数轴上,表示+2的点与原点的距离是多少?
(2)在数轴上,表示-2的点与原点的距离是多少?
(3)由此你能发现什么?
思考完成并交流展示.
活动3 知识归纳
1.一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,
记作 ,读作 .
2.一个正数的绝对值是 ;
一个负数的绝对值是 ;
0的绝对值是 .
即
|a|
它本身
它的相反数
a的绝对值
0
a
0
-a
活动3 知识归纳
3.(1)一个数的绝对值是 ;
(2)绝对值等于它本身的数是 ;
(3)绝对值等于它相反数的数是 .
非负数
非负数
非正数
活动4 例题与练习
例1 求下列各数的绝对值.
解:
(2) |-7.2|
=-(-7.2)
(3) |0|
=0.
(2)-7.2;
(1)
(3)0.
(1)
=7.2;
例2 计算.
解:原式
解:原式
(1)|-18|+|-6|;
=18+6
=24.
1.教材P11 练习第1,2 题.
练 习
2.下列说法正确的是 ( )
A.一个数的绝对值一定是正数
B.负数的绝对值等于它的相反数
C.一个数的绝对值一定是非正数
D.绝对值是它本身的数有两个,分别是0和1
B
练 习
3.下列各式中,不成立的是 ( )
A.|-5|=5 B.-|5|=-|-5|
C.|+5|=5 D.-|-5|=5
D
4.若|a|=8,则a= ;
若|-a|=8,则a= ;
若|a|=|-8|,则a= .
±8
±8
±8
练 习
5.蜗牛从点O开始沿东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数,爬过的各段路程依次为(单位:cm):
解:(1)5-3+10-8-6+12-10=0,
(2)∵+5+(-3)+(+10)=+12的绝对值最大,
∴蜗牛离开出发点O最远时是12 cm;
(3)∵1×(|+5|+|-3|+|+10|+|-8|+|-6|+|+12|+|-10|)=54(粒),
∴蜗牛最后回到出发点;
+5,-3,+10,-8,-6,+12,-10.
(1)蜗牛最后是否回到出发点?
(2)蜗牛离开出发点O最远时是多少厘米?
(3)在爬行过程中,如果每爬1 cm奖励一粒芝麻,则蜗牛一共得到多少粒芝麻?
∴蜗牛一共得到54粒芝麻.
1.2 有理数
1.2.4 绝对值
第1课时 绝对值
一、教学目标
1.理解绝对值的意义,使学生学会求一个数的绝对值.
2.通过观察、比较、归纳得出绝对值的概念,感受数形结合的思想.
重点
难点
理解绝对值的意义,会求一个数的绝对值.
对绝对值概念的理解.
二、教学重难点
活动1 新课导入
三、教学设计
1.10的相反数是 .
-10
答:-2的相反数是2;
2.-2,4, ,0,2 020的相反数分别是什么?
4的相反数是-4;
0的相反数是0;
2 020的相反数是-2 020.
的相反数是 ;
活动2 探究新知
1.教材P11 内容.
两辆汽车从同一处O出发,分别向东、西方向行使10 km ,到达A,B两处.
A
O
B
0
10
-10
图 1.2-6
活动2 探究新知
1.教材P11 内容.
提出问题:
思考完成并交流展示.
(2)甲、乙两辆汽车行驶的路程各是多少?它们行驶的路程相等吗?
(3)你还能列举出类似的例子吗?
(1)甲、乙两辆汽车的位置如何表示?它们的行驶路线相同吗?
活动2 探究新知
2.思考并回答下列问题:
(1)在数轴上,表示+2的点与原点的距离是多少?
(2)在数轴上,表示-2的点与原点的距离是多少?
(3)由此你能发现什么?
思考完成并交流展示.
活动3 知识归纳
1.一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,
记作 ,读作 .
2.一个正数的绝对值是 ;
一个负数的绝对值是 ;
0的绝对值是 .
即
|a|
它本身
它的相反数
a的绝对值
0
a
0
-a
活动3 知识归纳
3.(1)一个数的绝对值是 ;
(2)绝对值等于它本身的数是 ;
(3)绝对值等于它相反数的数是 .
非负数
非负数
非正数
活动4 例题与练习
例1 求下列各数的绝对值.
解:
(2) |-7.2|
=-(-7.2)
(3) |0|
=0.
(2)-7.2;
(1)
(3)0.
(1)
=7.2;
例2 计算.
解:原式
解:原式
(1)|-18|+|-6|;
=18+6
=24.
1.教材P11 练习第1,2 题.
练 习
2.下列说法正确的是 ( )
A.一个数的绝对值一定是正数
B.负数的绝对值等于它的相反数
C.一个数的绝对值一定是非正数
D.绝对值是它本身的数有两个,分别是0和1
B
练 习
3.下列各式中,不成立的是 ( )
A.|-5|=5 B.-|5|=-|-5|
C.|+5|=5 D.-|-5|=5
D
4.若|a|=8,则a= ;
若|-a|=8,则a= ;
若|a|=|-8|,则a= .
±8
±8
±8
练 习
5.蜗牛从点O开始沿东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数,爬过的各段路程依次为(单位:cm):
解:(1)5-3+10-8-6+12-10=0,
(2)∵+5+(-3)+(+10)=+12的绝对值最大,
∴蜗牛离开出发点O最远时是12 cm;
(3)∵1×(|+5|+|-3|+|+10|+|-8|+|-6|+|+12|+|-10|)=54(粒),
∴蜗牛最后回到出发点;
+5,-3,+10,-8,-6,+12,-10.
(1)蜗牛最后是否回到出发点?
(2)蜗牛离开出发点O最远时是多少厘米?
(3)在爬行过程中,如果每爬1 cm奖励一粒芝麻,则蜗牛一共得到多少粒芝麻?
∴蜗牛一共得到54粒芝麻.
