人教版数学七年级上册1.4.1 第1课时 有理数的乘法法则课件(22张)
文档属性
| 名称 | 人教版数学七年级上册1.4.1 第1课时 有理数的乘法法则课件(22张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-30 11:43:17 | ||
图片预览








文档简介
第一章 有理数
1. 4 有理数的乘除法
1. 4.1 有理数的乘法
第1课时 有理数的乘法法则
一、教学目标
1.理解有理数乘法的意义,掌握有理数乘法法则.
2.能准确地进行有理数的乘法运算,培养探索能力.
3.传授知识的同时,注意培养勇于探索新知的精神.
重点
难点
有理数的乘法法则.
有理数乘法中的符号法则.
二、教学重难点
一口深3.5米的深井,一只青蛙从井底沿井壁往上爬,第一次爬了0.7米又下滑了0.1米,第二次往上爬了0.42米又下滑了0.15米,第三次往上爬了1.25米又下滑了0.2米,第四次往上爬了0.75米又下滑了0.1米,第五次往上爬了0.65米.
问题:小青蛙爬出井了吗?
问题引入
活动1 新课导入
三、教学设计
1.口算:
(1)(-5)+(-5)= ;
(2)(-5)+(-5)+(-5)= ;
(3)(-5)+(-5)+(-5)+(-5)= ;
(4)(-5)+(-5)+(-5)+(-5)+(-5)= .
-10
-15
-20
-25
活动1 新课导入
三、教学设计
2.猜想下列各式的值:
(-5)×2= ;(-5)×3= ;
(-5)×4= ;(-5)×5= .
-10
-15
-20
-25
3.两个有理数相乘有几种情况?
答:五种:正数乘正数;负数乘负数;正数乘负数;正数乘0;负数乘0.
活动2 探究新知
提出问题:
(1)积的符号与因数的符号有什么关系?
(2)一个数和0相乘,结果是多少?
(3)由此你能得出什么结论?
思考完成并交流展示.
1.教材P28-29 内容.
2.教材P30 部分内容.
提出问题:
(1)有理数的乘法法则与小学的乘法法则有什么不同?
(2)倒数等于本身的数有哪些?
思考完成并交流展示.
活动2 探究新知
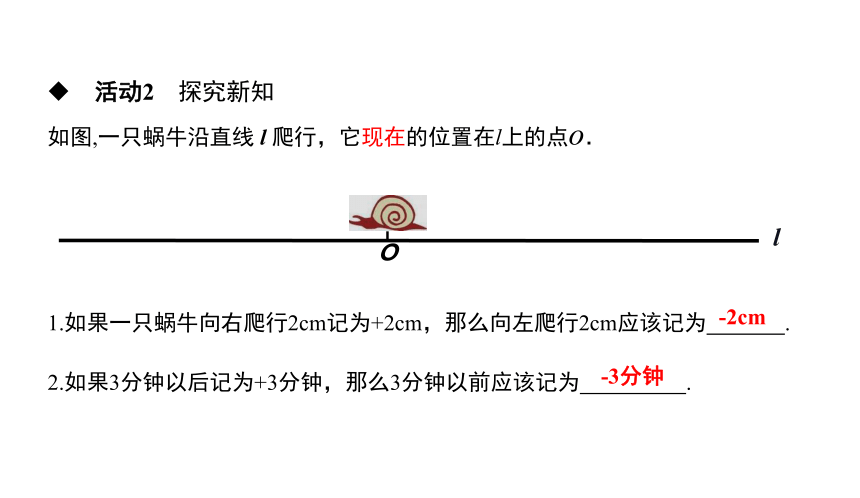
如图,一只蜗牛沿直线 l 爬行,它现在的位置在l上的点o.
l
O
1.如果一只蜗牛向右爬行2cm记为+2cm,那么向左爬行2cm应该记为 .
2.如果3分钟以后记为+3分钟,那么3分钟以前应该记为 .
-2cm
-3分钟
活动2 探究新知
(1)如果蜗牛一直以每分2cm的速度向右爬行,3分后它在什么位置?
(2)如果蜗牛一直以每分2cm的速度向左爬行,3分后它在什么位置?
(3)如果蜗牛一直以每分2cm的速度向右爬行,3分前它在什么位置?
(4)如果蜗牛一直以每分2cm的速度向左爬行,3分前它在什么位置?
(5)原地不动或运动了零次,结果是什么?
规定:向左为负,向右为正.现在前为负,现在后为正.
为了区分方向与时间:
思 考
2
0
2
6
4
l
结果:3分钟后在l上点O 边 cm处
表示: .
右
6
(+2)×(+3)= 6
①
(1)如果蜗牛一直以每分钟2cm的速度向右爬行,3分钟后它在什么位置?
探究1
(2)如果蜗牛一直以每分钟2 cm的速度向左爬行,3分钟后它在什么位置?
-6
-4
0
-2
2
l
结果:3分钟后在l上点O 边 cm处
左
6
表示: .
(-2)×(+3)=
②
-6
探究2
(3)如果蜗牛一直以每分钟2 cm的速度向右爬行,3分钟前它在什么位置?
2
-6
-4
0
-2
2
l
结果:3分钟前在l上点O 边 cm处
表示: .
(+2)×(-3)=
-6
左
6
③
探究3
(4)如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟前它在什么位置?
2
0
2
6
4
-2
l
结果:3钟分前在l上点O 边 cm处
右
6
表示: .
(-2)×(-3)=
④
+6
探究4
答:结果都是仍在原处,即结果都是 ,
若用式子表达:
(5)原地不动或运动了零次,结果是什么?
0×3=0;0×(-3)=0;
2×0=0;(-2)×0=0.
零
O
探究5
活动3 知识归纳
1.两数相乘,同号得 ,异号得 ,并把绝对值 .
正
2.任何数与0相乘,都得 .
3.乘积是 的两个数互为倒数.即当a≠0时,a的倒数是 .
负
相乘
0
1
(+2)×(+3)=+6 (-2)×(-3)=+6
(-2)×(+3)=-6 (+2)×(-3)=-6
2×0=0 (-2)×0=0
活动4 例题与练习
例1 计算:
(1) (-3)×9;
解: (1) (-3)×9
=-27
(2) 8×(-1) ;
(2) 8×(-1)
=-8
=1
要得到一个数的相反数,只要将它乘-1.
例2 用正负数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km,气温的变化量为-6℃,攀登3km后,气温有什么变化?
解:(-6)×3= -18
答:气温下降18℃.
解:由题意,得a+b=0,
cd=1,
x=-1,
∴原式=0+1-1=0.
例3 若a,b互为相反数,c,d互为倒数,x= ×2,求a+b+|x|-cd的值.
解:(1)7※(-3)
例4 规定一种新运算“※”,两数a,b通过“※”运算得(a+2)×2-b,即a※b=(a+2)×2-b,例如3※5=(3+2)×2-5=10-5=5.根据上面规定解答下题:
(1)求7※(-3)的值;
(2)7※(-3)与(-3)※7的值相等吗?
(2)∵(-3)※7
=(7+2)×2-(-3)
=21;
∴7※(-3)与(-3)※7的值不相等.
=[(-3)+2]×2-7
=-9,
1.教材P30 练习第1,2,3题.
练 习
3.如果a+b<0,ab>0,那么a,b这两个数 ( )
A.都是正数 B.都是负数
C.一正一负 D.符号无法确定
D
B
2.若□×(-2)=1,则在□内填一个数应是 ( )
4.如图,按下面程序计算,如果输入的数是-2,那么输出的 数是 .
练 习
-162
练 习
5.计算:
解:(1)原式=-27;
(1)(-3)×9; (2)(-0.01)×0; (3) ×(-2).
(2)原式=0;
(3)原式=1
1. 4 有理数的乘除法
1. 4.1 有理数的乘法
第1课时 有理数的乘法法则
一、教学目标
1.理解有理数乘法的意义,掌握有理数乘法法则.
2.能准确地进行有理数的乘法运算,培养探索能力.
3.传授知识的同时,注意培养勇于探索新知的精神.
重点
难点
有理数的乘法法则.
有理数乘法中的符号法则.
二、教学重难点
一口深3.5米的深井,一只青蛙从井底沿井壁往上爬,第一次爬了0.7米又下滑了0.1米,第二次往上爬了0.42米又下滑了0.15米,第三次往上爬了1.25米又下滑了0.2米,第四次往上爬了0.75米又下滑了0.1米,第五次往上爬了0.65米.
问题:小青蛙爬出井了吗?
问题引入
活动1 新课导入
三、教学设计
1.口算:
(1)(-5)+(-5)= ;
(2)(-5)+(-5)+(-5)= ;
(3)(-5)+(-5)+(-5)+(-5)= ;
(4)(-5)+(-5)+(-5)+(-5)+(-5)= .
-10
-15
-20
-25
活动1 新课导入
三、教学设计
2.猜想下列各式的值:
(-5)×2= ;(-5)×3= ;
(-5)×4= ;(-5)×5= .
-10
-15
-20
-25
3.两个有理数相乘有几种情况?
答:五种:正数乘正数;负数乘负数;正数乘负数;正数乘0;负数乘0.
活动2 探究新知
提出问题:
(1)积的符号与因数的符号有什么关系?
(2)一个数和0相乘,结果是多少?
(3)由此你能得出什么结论?
思考完成并交流展示.
1.教材P28-29 内容.
2.教材P30 部分内容.
提出问题:
(1)有理数的乘法法则与小学的乘法法则有什么不同?
(2)倒数等于本身的数有哪些?
思考完成并交流展示.
活动2 探究新知
如图,一只蜗牛沿直线 l 爬行,它现在的位置在l上的点o.
l
O
1.如果一只蜗牛向右爬行2cm记为+2cm,那么向左爬行2cm应该记为 .
2.如果3分钟以后记为+3分钟,那么3分钟以前应该记为 .
-2cm
-3分钟
活动2 探究新知
(1)如果蜗牛一直以每分2cm的速度向右爬行,3分后它在什么位置?
(2)如果蜗牛一直以每分2cm的速度向左爬行,3分后它在什么位置?
(3)如果蜗牛一直以每分2cm的速度向右爬行,3分前它在什么位置?
(4)如果蜗牛一直以每分2cm的速度向左爬行,3分前它在什么位置?
(5)原地不动或运动了零次,结果是什么?
规定:向左为负,向右为正.现在前为负,现在后为正.
为了区分方向与时间:
思 考
2
0
2
6
4
l
结果:3分钟后在l上点O 边 cm处
表示: .
右
6
(+2)×(+3)= 6
①
(1)如果蜗牛一直以每分钟2cm的速度向右爬行,3分钟后它在什么位置?
探究1
(2)如果蜗牛一直以每分钟2 cm的速度向左爬行,3分钟后它在什么位置?
-6
-4
0
-2
2
l
结果:3分钟后在l上点O 边 cm处
左
6
表示: .
(-2)×(+3)=
②
-6
探究2
(3)如果蜗牛一直以每分钟2 cm的速度向右爬行,3分钟前它在什么位置?
2
-6
-4
0
-2
2
l
结果:3分钟前在l上点O 边 cm处
表示: .
(+2)×(-3)=
-6
左
6
③
探究3
(4)如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟前它在什么位置?
2
0
2
6
4
-2
l
结果:3钟分前在l上点O 边 cm处
右
6
表示: .
(-2)×(-3)=
④
+6
探究4
答:结果都是仍在原处,即结果都是 ,
若用式子表达:
(5)原地不动或运动了零次,结果是什么?
0×3=0;0×(-3)=0;
2×0=0;(-2)×0=0.
零
O
探究5
活动3 知识归纳
1.两数相乘,同号得 ,异号得 ,并把绝对值 .
正
2.任何数与0相乘,都得 .
3.乘积是 的两个数互为倒数.即当a≠0时,a的倒数是 .
负
相乘
0
1
(+2)×(+3)=+6 (-2)×(-3)=+6
(-2)×(+3)=-6 (+2)×(-3)=-6
2×0=0 (-2)×0=0
活动4 例题与练习
例1 计算:
(1) (-3)×9;
解: (1) (-3)×9
=-27
(2) 8×(-1) ;
(2) 8×(-1)
=-8
=1
要得到一个数的相反数,只要将它乘-1.
例2 用正负数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km,气温的变化量为-6℃,攀登3km后,气温有什么变化?
解:(-6)×3= -18
答:气温下降18℃.
解:由题意,得a+b=0,
cd=1,
x=-1,
∴原式=0+1-1=0.
例3 若a,b互为相反数,c,d互为倒数,x= ×2,求a+b+|x|-cd的值.
解:(1)7※(-3)
例4 规定一种新运算“※”,两数a,b通过“※”运算得(a+2)×2-b,即a※b=(a+2)×2-b,例如3※5=(3+2)×2-5=10-5=5.根据上面规定解答下题:
(1)求7※(-3)的值;
(2)7※(-3)与(-3)※7的值相等吗?
(2)∵(-3)※7
=(7+2)×2-(-3)
=21;
∴7※(-3)与(-3)※7的值不相等.
=[(-3)+2]×2-7
=-9,
1.教材P30 练习第1,2,3题.
练 习
3.如果a+b<0,ab>0,那么a,b这两个数 ( )
A.都是正数 B.都是负数
C.一正一负 D.符号无法确定
D
B
2.若□×(-2)=1,则在□内填一个数应是 ( )
4.如图,按下面程序计算,如果输入的数是-2,那么输出的 数是 .
练 习
-162
练 习
5.计算:
解:(1)原式=-27;
(1)(-3)×9; (2)(-0.01)×0; (3) ×(-2).
(2)原式=0;
(3)原式=1
