人教版数学七年级上册1.5.1 第1课时 有理数的乘方课件(13张)
文档属性
| 名称 | 人教版数学七年级上册1.5.1 第1课时 有理数的乘方课件(13张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 817.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-30 00:00:00 | ||
图片预览





文档简介
第一章 有理数
1. 5 有理数的乘方
1.5.1 乘方
第1课时 有理数的乘方
一、教学目标
1.理解有理数的乘方、幂、底数、指数的概念及其相互间的关系,会进行乘方的运算.
2.在生动的情境中让学生获得有理数乘方的初步经验;培养学生观察、分析、归纳、概括的能力;经历从乘法到乘方的推广过程,从中感受化归的数学思想.
重点
难点
乘方的相关概念及运算方法.
理解有理数的乘方、幂、底数、指数的概念及其相互间的关系.
二、教学重难点
活动1 新课导入
三、教学设计
1.长为2的正方形,它的面积是多少?
解:2×2=4.
2.边长为l的正方体,它的体积是多少?
解:l×l×l=l3.
活动2 探究新知
1.教材P41 内容.
提出问题:
(1)2个2相乘记作22,3个2相乘记作23,n个2相乘记作多少?
(2)引入负数后,4个-2相乘记作多少?-24和(-2)4一样吗?为什么?
(3)求n个相同因数的积的运算,叫做什么?它们的结果又叫做什么?
(4)在an中,a和n分别叫做什么?
活动2 探究新知
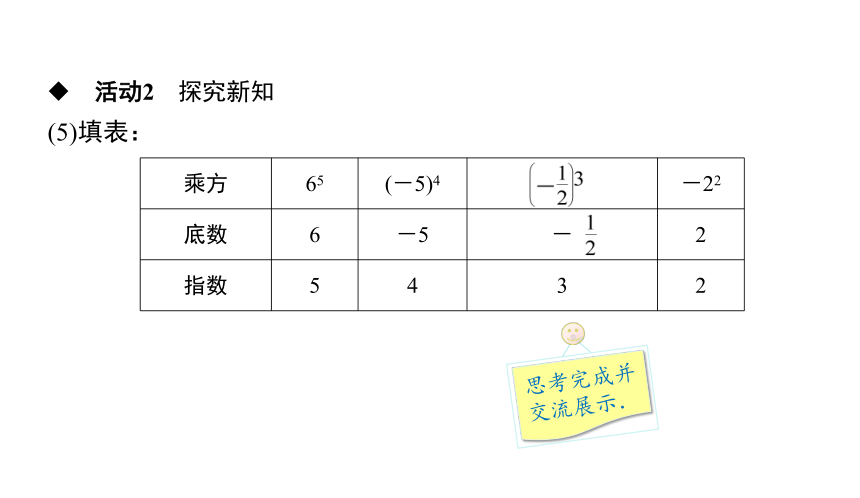
(5)填表:
思考完成并交流展示.
乘方
65
(-5)4
-22
底数
6
-5
-
2
指数
5
4
3
2
活动2 探究新知
2.教材P42 思考.
从例1,你发现负数的幂的正负有什么规律?
当指数是_____数时,负数的幂是_____数;
当指数是_____数时,负数的幂是_____数.
根据有理数的乘法法则可以得出:
负数的奇次幂是负数,负数的偶次幂是正数。
显然,正数的任何次幂都是正数,0的任何正整数次幂都是0
思考完成并交流展示.
活动3 知识归纳
1.一般地,n个相同的因数a相乘,即 记作____,
读作_____________,其中a叫做______,n叫做_______.求n个相同因数的____的运算,叫做乘方,乘方的结果叫做____.
an
“a的n次方”
底数
指数
积
幂
2.负数的奇次幂是______,负数的偶次幂是_______.正数的任何次幂都是_______,0的任何正整数次幂都是____.
负数
正数
正数
0
活动4 例题与练习
例1 计算:
(1) (-4)3; (2) (-2)4; (3)
解:(1) (-4)3=(-4)×(-4)×(-4)=-64;
(2) (-2)4=(-2)×(-2)×(-2)×(-2)=16;
例2 化简下列分数:
例2 用计算器计算(-8)5和(-3)6.
解:用带符号键 的计算器.
(-)
=
)
(-)
(
<
8
5
显示:(-8) 5
<
-32768.
=
)
(-)
(
<
3
6
显示:(-3) 6
<
729.
所以(-8)5=-32768, (-3)6=729.
例3
算式 可表示为( )
A
例4 计算:
解:原式=- ;
(2)-24×(-2)2;
解:原式=-64;
(3)-42×(-4)2;
解:原式=-256;
解:原式=- ;
解:原式=-1;
解:原式= ;
1.教材P42~43 练习第1,2,3题.
练 习
2.关于-74的说法正确的是( )
A.底数是-7 B.表示4个-7相乘
C.表示4个7相乘的相反数 D.表示7个-4相乘
C
3.下列各组数中,相等的一组是( )
A.23与32 B.23与(-2)3 C.32与(-3)2 D.-23与-33
C
练 习
4.(1)平方等于本身的数是______,立方等于本身的数是___________;
(2)平方等于64的数是____,立方等于-64的数是____;
(3)定义一种新的运算a&b=ab,如2&3=23=8,那么(3&2)&2=____.
0或1
0或±1
±8
-4
81
1. 5 有理数的乘方
1.5.1 乘方
第1课时 有理数的乘方
一、教学目标
1.理解有理数的乘方、幂、底数、指数的概念及其相互间的关系,会进行乘方的运算.
2.在生动的情境中让学生获得有理数乘方的初步经验;培养学生观察、分析、归纳、概括的能力;经历从乘法到乘方的推广过程,从中感受化归的数学思想.
重点
难点
乘方的相关概念及运算方法.
理解有理数的乘方、幂、底数、指数的概念及其相互间的关系.
二、教学重难点
活动1 新课导入
三、教学设计
1.长为2的正方形,它的面积是多少?
解:2×2=4.
2.边长为l的正方体,它的体积是多少?
解:l×l×l=l3.
活动2 探究新知
1.教材P41 内容.
提出问题:
(1)2个2相乘记作22,3个2相乘记作23,n个2相乘记作多少?
(2)引入负数后,4个-2相乘记作多少?-24和(-2)4一样吗?为什么?
(3)求n个相同因数的积的运算,叫做什么?它们的结果又叫做什么?
(4)在an中,a和n分别叫做什么?
活动2 探究新知
(5)填表:
思考完成并交流展示.
乘方
65
(-5)4
-22
底数
6
-5
-
2
指数
5
4
3
2
活动2 探究新知
2.教材P42 思考.
从例1,你发现负数的幂的正负有什么规律?
当指数是_____数时,负数的幂是_____数;
当指数是_____数时,负数的幂是_____数.
根据有理数的乘法法则可以得出:
负数的奇次幂是负数,负数的偶次幂是正数。
显然,正数的任何次幂都是正数,0的任何正整数次幂都是0
思考完成并交流展示.
活动3 知识归纳
1.一般地,n个相同的因数a相乘,即 记作____,
读作_____________,其中a叫做______,n叫做_______.求n个相同因数的____的运算,叫做乘方,乘方的结果叫做____.
an
“a的n次方”
底数
指数
积
幂
2.负数的奇次幂是______,负数的偶次幂是_______.正数的任何次幂都是_______,0的任何正整数次幂都是____.
负数
正数
正数
0
活动4 例题与练习
例1 计算:
(1) (-4)3; (2) (-2)4; (3)
解:(1) (-4)3=(-4)×(-4)×(-4)=-64;
(2) (-2)4=(-2)×(-2)×(-2)×(-2)=16;
例2 化简下列分数:
例2 用计算器计算(-8)5和(-3)6.
解:用带符号键 的计算器.
(-)
=
)
(-)
(
<
8
5
显示:(-8) 5
<
-32768.
=
)
(-)
(
<
3
6
显示:(-3) 6
<
729.
所以(-8)5=-32768, (-3)6=729.
例3
算式 可表示为( )
A
例4 计算:
解:原式=- ;
(2)-24×(-2)2;
解:原式=-64;
(3)-42×(-4)2;
解:原式=-256;
解:原式=- ;
解:原式=-1;
解:原式= ;
1.教材P42~43 练习第1,2,3题.
练 习
2.关于-74的说法正确的是( )
A.底数是-7 B.表示4个-7相乘
C.表示4个7相乘的相反数 D.表示7个-4相乘
C
3.下列各组数中,相等的一组是( )
A.23与32 B.23与(-2)3 C.32与(-3)2 D.-23与-33
C
练 习
4.(1)平方等于本身的数是______,立方等于本身的数是___________;
(2)平方等于64的数是____,立方等于-64的数是____;
(3)定义一种新的运算a&b=ab,如2&3=23=8,那么(3&2)&2=____.
0或1
0或±1
±8
-4
81
