人教版数学七年级上册3.3 第1课时 去括号解一元一次方程课件(15张)
文档属性
| 名称 | 人教版数学七年级上册3.3 第1课时 去括号解一元一次方程课件(15张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-30 12:03:49 | ||
图片预览






文档简介
3.3 解一元一次方程(二)——去括号与去分母
第1课时 去括号解一元一次方程
一、教学目标
重点
难点
二、教学重难点
1.掌握去括号法则,并能熟练运用去括号解一元一次方程.
2.掌握去括号解一元一次方程的一般步骤,能熟练地解含括号的一元一次方程.
3.明确复杂问题中的数量关系,准确列出方程.
去括号法则.
针对实际问题列方程,并用去括号法则解一元一次方程.
三、教学设计
活动1 新课导入
1.某制衣厂生产儿童套装,去年下半年与上半年相比,月平均生产量减少500套,去年全年生产21 000套,这个制衣厂去年上半年每月平均生产多少套?(只列方程,不解答)
解:设去年上半年每月平均生产x套,则下半年每月平均生产(x-500)套.
由题意,得6x+6(x-500)=21 000.
思考:如何将方程转化为x=a的形式?
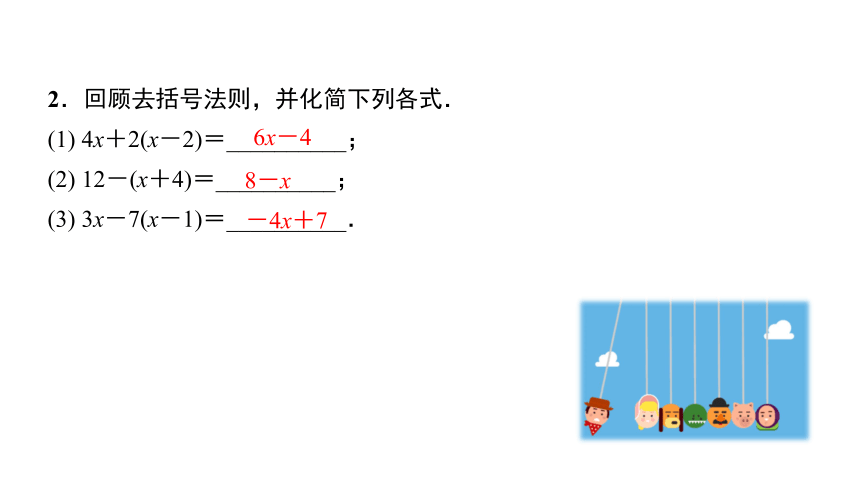
2.回顾去括号法则,并化简下列各式.
(1) 4x+2(x-2)=__________;
(2) 12-(x+4)=__________;
(3) 3x-7(x-1)=__________.
6x-4
8-x
-4x+7
活动2 探究新知
1.教材P93 问题1.
提出问题:
(1)本题的等量关系是什么?如何列方程?
(2)该方程与之前学过的方程有什么不同?
(3)如何解这种类型的方程?
(4)去括号时最容易出错的地方是什么?
分析答案,提出疑惑,共同解决.
2.教材P93 思考.
活动3 知识归纳
1.行程问题中,常用的等量关系:
(1)路程=_______×_______;
(2)顺流、逆流问题:
①顺流速度=静水中的速度_______水流速度;
②逆流速度=静水中的速度_______水流程度;
③往返等路程问题:顺流速度×顺流时间=逆流速度×_____________.
速度
时间
+
-
逆流时间
2.解方程过程中,去掉括号的过程和整式运算中的去括号法则______.
3.去括号解一元一次方程的步骤为:
①去括号;
②_______;
③_____________;
④________________.
相同
移项
合并同类项
系数化为1
解下列方程:
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
活动4 例题与练习
例1 教材P94 例1.
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
例2
分析:等量关系:这艘船往返的路程相等,即
顺流速度___顺流时间___逆流速度___逆流时间
×
=
×
一艘船从甲码头到乙码头顺流行驶,用了2 h;从乙码头返回甲码头逆流行驶,用了2.5 h.已知水流的速度是3 km/h,求船在静水中的速度?
解:设船在静水中的平均速度为x km/h,则顺流的速度为(x+3) km/h,逆流速度为(x-3) km/h.
去括号,得
移项及合并同类项,得
系数化为1,得
答:船在静水中的平均速度为 27 km/h.
×
根据顺流速度___顺流时间___逆流速度 ___逆流时间
列出方程,得
×
=
例3 定义一种新运算“⊕”:a⊕b=a-2b,
比如:2⊕(-3)=2-2×(-3)=2+6=8.
(1)求(-3)⊕2的值;
(2)若(x-3)⊕(x+1)=1,求x的值.
解:(1) (-3)⊕2=-3-2×2=-7;
(2) (x-3)⊕(x+1)=(x-3)-2(x+1)=1,解得x=-6.
练 习
1.教材P95 练习.
2.下列是四位同学解方程2(x-2)-3(4x-1)=9时,去括号的结果,其中正确的是( )
A.2x-4-12x+3=9 B.2x-4-12x-3=9
C.2x-4-12x+1=9 D.2x-2-12x+1=9
A
3.解方程
的步骤如下:
①去括号,得4x-4-x=2x+1;②移项,得4x+x-2x=1+4;③合并同类项,得3x=5;④系数化为1,得
其中开始出现错误的一步是( )
A.① B. ② C . ③ D.④
B
4.一个两位数,十位数字与个位数字的和是7.如果把两个数位上的数字对调,所得两位数比原数大45,那么原两位数是____.
16
5.已知x=3(9-a)-7(-7+a),y=21+5(a-4),当a为何值时,x与y相等?
解:∵x=y,∴3(9-a)-7(-7+a)=21+5(a-4).
去括号,得27-3a+49-7a=21+5a-20.
移项,得-3a-7a-5a=21-20-27-49.
合并同类项,得-15a=-75.
系数化为1,得a=5.
∴当a=5时,x=y.
第1课时 去括号解一元一次方程
一、教学目标
重点
难点
二、教学重难点
1.掌握去括号法则,并能熟练运用去括号解一元一次方程.
2.掌握去括号解一元一次方程的一般步骤,能熟练地解含括号的一元一次方程.
3.明确复杂问题中的数量关系,准确列出方程.
去括号法则.
针对实际问题列方程,并用去括号法则解一元一次方程.
三、教学设计
活动1 新课导入
1.某制衣厂生产儿童套装,去年下半年与上半年相比,月平均生产量减少500套,去年全年生产21 000套,这个制衣厂去年上半年每月平均生产多少套?(只列方程,不解答)
解:设去年上半年每月平均生产x套,则下半年每月平均生产(x-500)套.
由题意,得6x+6(x-500)=21 000.
思考:如何将方程转化为x=a的形式?
2.回顾去括号法则,并化简下列各式.
(1) 4x+2(x-2)=__________;
(2) 12-(x+4)=__________;
(3) 3x-7(x-1)=__________.
6x-4
8-x
-4x+7
活动2 探究新知
1.教材P93 问题1.
提出问题:
(1)本题的等量关系是什么?如何列方程?
(2)该方程与之前学过的方程有什么不同?
(3)如何解这种类型的方程?
(4)去括号时最容易出错的地方是什么?
分析答案,提出疑惑,共同解决.
2.教材P93 思考.
活动3 知识归纳
1.行程问题中,常用的等量关系:
(1)路程=_______×_______;
(2)顺流、逆流问题:
①顺流速度=静水中的速度_______水流速度;
②逆流速度=静水中的速度_______水流程度;
③往返等路程问题:顺流速度×顺流时间=逆流速度×_____________.
速度
时间
+
-
逆流时间
2.解方程过程中,去掉括号的过程和整式运算中的去括号法则______.
3.去括号解一元一次方程的步骤为:
①去括号;
②_______;
③_____________;
④________________.
相同
移项
合并同类项
系数化为1
解下列方程:
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
活动4 例题与练习
例1 教材P94 例1.
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
例2
分析:等量关系:这艘船往返的路程相等,即
顺流速度___顺流时间___逆流速度___逆流时间
×
=
×
一艘船从甲码头到乙码头顺流行驶,用了2 h;从乙码头返回甲码头逆流行驶,用了2.5 h.已知水流的速度是3 km/h,求船在静水中的速度?
解:设船在静水中的平均速度为x km/h,则顺流的速度为(x+3) km/h,逆流速度为(x-3) km/h.
去括号,得
移项及合并同类项,得
系数化为1,得
答:船在静水中的平均速度为 27 km/h.
×
根据顺流速度___顺流时间___逆流速度 ___逆流时间
列出方程,得
×
=
例3 定义一种新运算“⊕”:a⊕b=a-2b,
比如:2⊕(-3)=2-2×(-3)=2+6=8.
(1)求(-3)⊕2的值;
(2)若(x-3)⊕(x+1)=1,求x的值.
解:(1) (-3)⊕2=-3-2×2=-7;
(2) (x-3)⊕(x+1)=(x-3)-2(x+1)=1,解得x=-6.
练 习
1.教材P95 练习.
2.下列是四位同学解方程2(x-2)-3(4x-1)=9时,去括号的结果,其中正确的是( )
A.2x-4-12x+3=9 B.2x-4-12x-3=9
C.2x-4-12x+1=9 D.2x-2-12x+1=9
A
3.解方程
的步骤如下:
①去括号,得4x-4-x=2x+1;②移项,得4x+x-2x=1+4;③合并同类项,得3x=5;④系数化为1,得
其中开始出现错误的一步是( )
A.① B. ② C . ③ D.④
B
4.一个两位数,十位数字与个位数字的和是7.如果把两个数位上的数字对调,所得两位数比原数大45,那么原两位数是____.
16
5.已知x=3(9-a)-7(-7+a),y=21+5(a-4),当a为何值时,x与y相等?
解:∵x=y,∴3(9-a)-7(-7+a)=21+5(a-4).
去括号,得27-3a+49-7a=21+5a-20.
移项,得-3a-7a-5a=21-20-27-49.
合并同类项,得-15a=-75.
系数化为1,得a=5.
∴当a=5时,x=y.
