人教版数学七年级上册4.1.1 第2课时 折叠、展开与从不同方向观察立体图形课件(11张)
文档属性
| 名称 | 人教版数学七年级上册4.1.1 第2课时 折叠、展开与从不同方向观察立体图形课件(11张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 561.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-30 00:00:00 | ||
图片预览



文档简介
第四章 几何图形初步
4.1 几何图形
4.1.1 立体图形与平面图形
第2课时 折叠、展开与从不同方向观察立体图形
一、教学目标
1.画出从不同方向看一些基本几何体以及它们的简单组合体得到的平面图形.
2.了解直棱柱、圆柱、圆锥的表面展开图,并能根据展开图想象相应的几何体,制作立体图形,在平面图形和立体图形相互转化的过程中,培养学生的空间观念和空间想象力.
重点
难点
从不同方向看一些简单几何体或它们的组合体得到平面图形.
根据展开图想象相应的几何体.
二、教学重难点
活动1 新课导入
三、教学设计
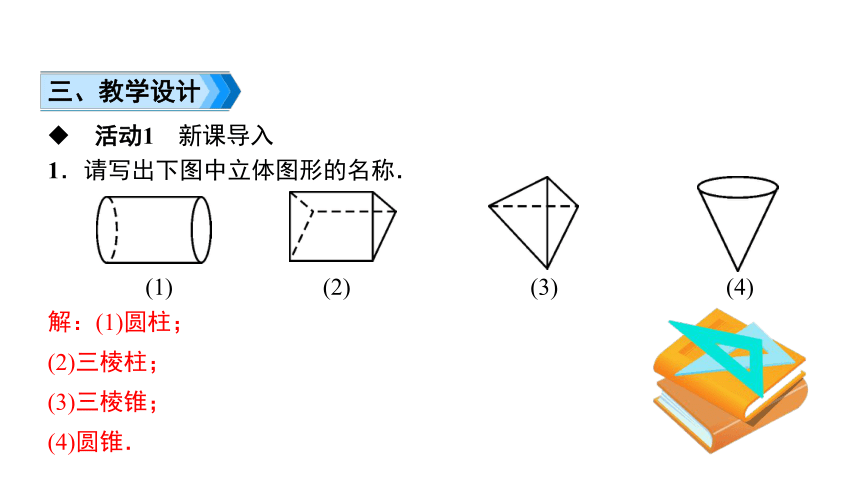
1.请写出下图中立体图形的名称.
解:(1)圆柱;
(2)三棱柱;
(3)三棱锥;
(4)圆锥.
(1) (2) (3) (4)
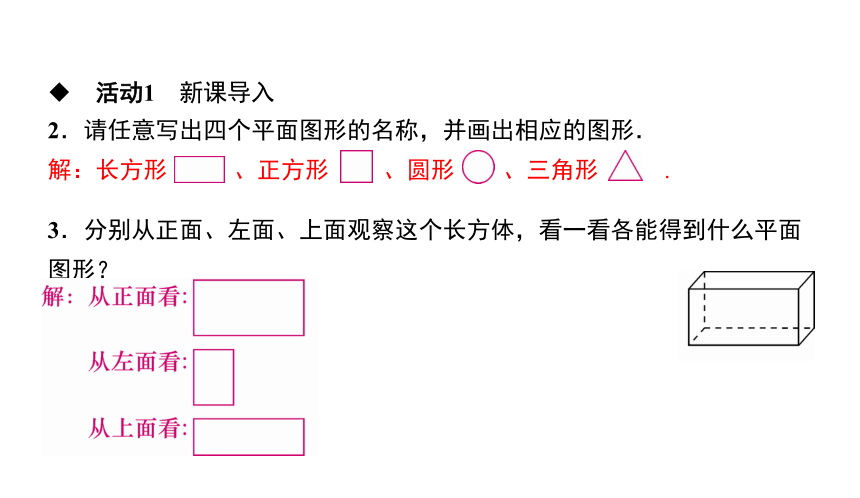
2.请任意写出四个平面图形的名称,并画出相应的图形.
解:长方形 、正方形 、圆形 、三角形 .
3.分别从正面、左面、上面观察这个长方体,看一看各能得到什么平面图形?
活动1 新课导入
活动2 探究新知
1.教材P117 探究.
提出问题:
(1) (1)一般从哪三个方向看立体图形?
(2)从不同的方向看图4.1-7,看到的图形是什么?它们的形状相同吗?
(3)你能画出从三个方向看到的图形吗?
思考完成并交流展示.
活动2 探究新知
2.教材P117 探究以下内容.
3.教材P118 探究.
提出问题:
(1)你知道墨水瓶包装盒是如何制造出来的吗?
(2)什么是立体图形的展开图?
(3)图中的墨水瓶包装盒的展开图是由哪些平面图形组成的?
(4)同一个立体图形,按不同的方式展开,得到的展开图是否一样?
活动3 知识归纳
1.对于一些立体图形的问题,常把它们转化为 来研究和处理.从不同的方向看立体图形,将会得到它们的平面图形.通常我们是从 、 、 三个方向看,从而得到相应的平面图形.
2.有些立体图形是由一些平面图形围成的,将它们的表面适当剪开,可以展开成 图形.这样的平面图形称为相应立体图形的
图.
平面图形
正面
左面
上面
平面
展开
活动4 例题与练习
例1 下列几何体中,从正面看是圆的是( )
B
A B C D
例2 如图是一个由9个正方体组成的立体图形,分别从正面、左面、上面观察这个图形,各能得到什么平面图形?
解:
例3 如图是由两个长方体组合而成的一个立体图形从三个方向看得到的平面图形,根据图中所标尺寸(单位:mm),求这个立体图形的表面积.
解:根据从三个方向看得到的平面图形可得,上面的长方体长4 mm、高4 mm、宽2 mm,下面的长方体长8 mm、宽6 mm、高2 mm,
∴这个立体图形的表面积是4×4×2+4×2×2+4×2+6×2×2+8×2×2+6×8×2-4×2=200(mm2).
1.教材P118-119 练习第1,2 ,3题.
练 习
2.如图所示的几何体,从左面看到的平面图形是( )
C
A B C D
4.1 几何图形
4.1.1 立体图形与平面图形
第2课时 折叠、展开与从不同方向观察立体图形
一、教学目标
1.画出从不同方向看一些基本几何体以及它们的简单组合体得到的平面图形.
2.了解直棱柱、圆柱、圆锥的表面展开图,并能根据展开图想象相应的几何体,制作立体图形,在平面图形和立体图形相互转化的过程中,培养学生的空间观念和空间想象力.
重点
难点
从不同方向看一些简单几何体或它们的组合体得到平面图形.
根据展开图想象相应的几何体.
二、教学重难点
活动1 新课导入
三、教学设计
1.请写出下图中立体图形的名称.
解:(1)圆柱;
(2)三棱柱;
(3)三棱锥;
(4)圆锥.
(1) (2) (3) (4)
2.请任意写出四个平面图形的名称,并画出相应的图形.
解:长方形 、正方形 、圆形 、三角形 .
3.分别从正面、左面、上面观察这个长方体,看一看各能得到什么平面图形?
活动1 新课导入
活动2 探究新知
1.教材P117 探究.
提出问题:
(1) (1)一般从哪三个方向看立体图形?
(2)从不同的方向看图4.1-7,看到的图形是什么?它们的形状相同吗?
(3)你能画出从三个方向看到的图形吗?
思考完成并交流展示.
活动2 探究新知
2.教材P117 探究以下内容.
3.教材P118 探究.
提出问题:
(1)你知道墨水瓶包装盒是如何制造出来的吗?
(2)什么是立体图形的展开图?
(3)图中的墨水瓶包装盒的展开图是由哪些平面图形组成的?
(4)同一个立体图形,按不同的方式展开,得到的展开图是否一样?
活动3 知识归纳
1.对于一些立体图形的问题,常把它们转化为 来研究和处理.从不同的方向看立体图形,将会得到它们的平面图形.通常我们是从 、 、 三个方向看,从而得到相应的平面图形.
2.有些立体图形是由一些平面图形围成的,将它们的表面适当剪开,可以展开成 图形.这样的平面图形称为相应立体图形的
图.
平面图形
正面
左面
上面
平面
展开
活动4 例题与练习
例1 下列几何体中,从正面看是圆的是( )
B
A B C D
例2 如图是一个由9个正方体组成的立体图形,分别从正面、左面、上面观察这个图形,各能得到什么平面图形?
解:
例3 如图是由两个长方体组合而成的一个立体图形从三个方向看得到的平面图形,根据图中所标尺寸(单位:mm),求这个立体图形的表面积.
解:根据从三个方向看得到的平面图形可得,上面的长方体长4 mm、高4 mm、宽2 mm,下面的长方体长8 mm、宽6 mm、高2 mm,
∴这个立体图形的表面积是4×4×2+4×2×2+4×2+6×2×2+8×2×2+6×8×2-4×2=200(mm2).
1.教材P118-119 练习第1,2 ,3题.
练 习
2.如图所示的几何体,从左面看到的平面图形是( )
C
A B C D
