人教版数学七年级上册4.1.2 点、线、面、体课件(12张)
文档属性
| 名称 | 人教版数学七年级上册4.1.2 点、线、面、体课件(12张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 742.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-30 12:08:36 | ||
图片预览




文档简介
第四章 几何图形初步
4.1 几何图形
4.1.2 点、线、面、体
一、教学目标
1.通过丰富的实例能正确判定围成几何体的面是平面还是曲面.
2.通过对点、线、面、体几何特征的认识,能正确判定由点、线、面、体经过运动变化形成的简单的几何图形.
重点
难点
正确判定围成立体图形的面是平面还是曲面,感受点、线、面、体之间的关系.
在实际背景中体会点的含义.
二、教学重难点
活动1 新课导入
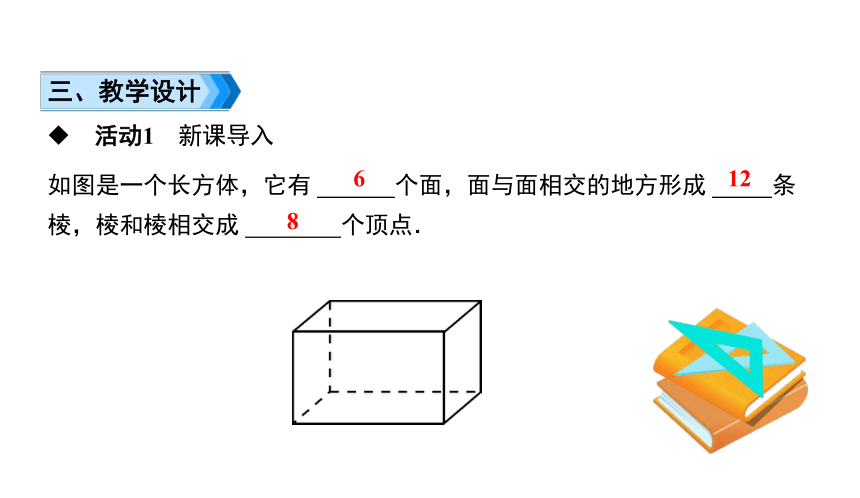
三、教学设计
如图是一个长方体,它有 个面,面与面相交的地方形成 条棱,棱和棱相交成 个顶点.
6
12
8
活动2 探究新知
1.教材P119 思考以下内容.
提出问题:
(1)长方体有几个面?
(2)长方体的面与面相交的地方形成几条棱?棱和棱相交形成几个顶点?
(3)由此可以得出几何图形是由哪些部分组成?
(4)点、线、面经过运动变化,形成的图形分别是什么?
思考完成并交流展示.
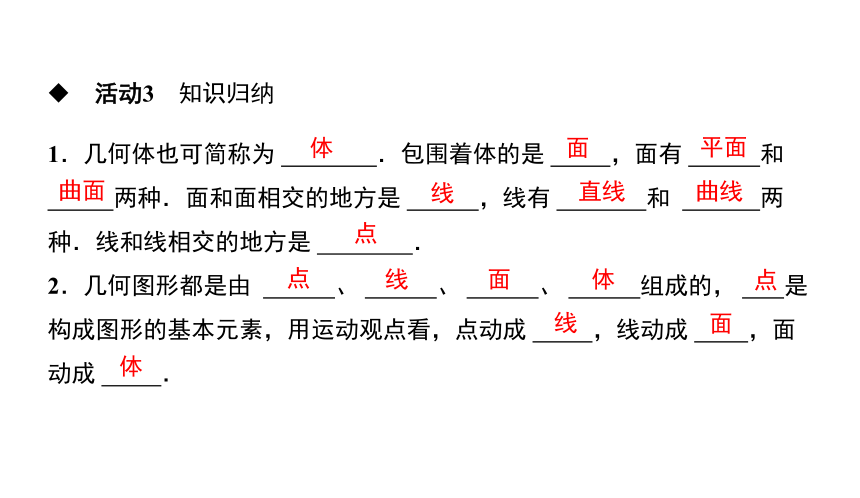
活动3 知识归纳
1.几何体也可简称为 .包围着体的是 ,面有 和
两种.面和面相交的地方是 ,线有 和 两种.线和线相交的地方是 .
2.几何图形都是由 、 、 、 组成的, 是构成图形的基本元素,用运动观点看,点动成 ,线动成 ,面动成 .
体
面
平面
曲面
线
直线
曲线
点
点
线
面
体
点
线
面
体
活动4 例题与练习
例1 观察图形,回答下列问题:
(1)图①是由几个面组成的,这些面有什么特征?
(2)图②是由几个面组成的,这些面有什么特征?
(3)图①中共有多少条线?这些线都是直的吗?图②呢?
(4)图①和图②中各有几个顶点?
解:(1)图①是由6个面组成的,这些面都是平面;
(2)图②是由2个面组成的,1个平面和1个曲面;
(3)图①中共有12条线,这些线都是直的;图②中有1条线,是曲线;
(4)图①中有8个顶点,图②中只有1个顶点.
例2 如图,上面的平面图形绕轴旋转一周,可以得出下面的立体图形,把有对应关系的平面图形与立体图形连接起来.
例3 笔尖画线可以理解为点动成线,请用数学知识解释下列生活中的现象.
(1)流星划破夜空,留下美丽的弧线;
(2)一条拉直的细线切开了一块豆腐;
(3)把一枚硬币立在桌面上用力一转,形成一个球.
解:(1)点动成线;
(2)线动成面;
(3)面动成体.
1.教材P120 练习第1题.
练 习
2.在球、圆锥、圆柱、棱柱中,由曲面和平面围成的是( )
A.球和圆锥 B.球和圆柱
C.圆锥和圆柱 D.圆柱和棱柱
3.下雨时,司机会打开雨刷器,雨刷器在运动时会形成一个扇面,这是因为( )
A.点动成线 B.线动成面
C.面动成体 D.面面相交形成线
B
C
4.如果一个多面体的一个面是多边形,其余各面都是有一个公共顶点的三角形,那么这个多面体叫做棱锥.如图是一个四棱柱和一个六棱锥,它们都有12条棱.下列棱柱中和九棱锥的棱数相等的是( )
练 习
B
A.五棱柱 B.六棱柱 C.七棱柱 D.八棱柱
练 习
5.如图所示的五棱柱,它的底面边长都是6 cm,侧棱长是8 cm,试回答下列问题:
(1)图中的五棱柱共有多少条棱?它们的长度分别是多少?
(2)图中的五棱柱共有多少个面?它们分别是什么形状?哪些面的形状和大小完全相同?
(3)求这个五棱柱的侧面积.
解:(1)五棱柱共有15条棱,侧面和上、下底面相交的棱长为6 cm,共10条;侧棱长均为8 cm,共5条;
(2)五棱柱共有7个面,底面都是五边形,侧面都是长方形;上、下底面的形状和大小完全相同,各个侧面的形状和大小完全相同;
(3)这个五棱柱的侧面积为6×8×5=240(cm2).
练 习
4.1 几何图形
4.1.2 点、线、面、体
一、教学目标
1.通过丰富的实例能正确判定围成几何体的面是平面还是曲面.
2.通过对点、线、面、体几何特征的认识,能正确判定由点、线、面、体经过运动变化形成的简单的几何图形.
重点
难点
正确判定围成立体图形的面是平面还是曲面,感受点、线、面、体之间的关系.
在实际背景中体会点的含义.
二、教学重难点
活动1 新课导入
三、教学设计
如图是一个长方体,它有 个面,面与面相交的地方形成 条棱,棱和棱相交成 个顶点.
6
12
8
活动2 探究新知
1.教材P119 思考以下内容.
提出问题:
(1)长方体有几个面?
(2)长方体的面与面相交的地方形成几条棱?棱和棱相交形成几个顶点?
(3)由此可以得出几何图形是由哪些部分组成?
(4)点、线、面经过运动变化,形成的图形分别是什么?
思考完成并交流展示.
活动3 知识归纳
1.几何体也可简称为 .包围着体的是 ,面有 和
两种.面和面相交的地方是 ,线有 和 两种.线和线相交的地方是 .
2.几何图形都是由 、 、 、 组成的, 是构成图形的基本元素,用运动观点看,点动成 ,线动成 ,面动成 .
体
面
平面
曲面
线
直线
曲线
点
点
线
面
体
点
线
面
体
活动4 例题与练习
例1 观察图形,回答下列问题:
(1)图①是由几个面组成的,这些面有什么特征?
(2)图②是由几个面组成的,这些面有什么特征?
(3)图①中共有多少条线?这些线都是直的吗?图②呢?
(4)图①和图②中各有几个顶点?
解:(1)图①是由6个面组成的,这些面都是平面;
(2)图②是由2个面组成的,1个平面和1个曲面;
(3)图①中共有12条线,这些线都是直的;图②中有1条线,是曲线;
(4)图①中有8个顶点,图②中只有1个顶点.
例2 如图,上面的平面图形绕轴旋转一周,可以得出下面的立体图形,把有对应关系的平面图形与立体图形连接起来.
例3 笔尖画线可以理解为点动成线,请用数学知识解释下列生活中的现象.
(1)流星划破夜空,留下美丽的弧线;
(2)一条拉直的细线切开了一块豆腐;
(3)把一枚硬币立在桌面上用力一转,形成一个球.
解:(1)点动成线;
(2)线动成面;
(3)面动成体.
1.教材P120 练习第1题.
练 习
2.在球、圆锥、圆柱、棱柱中,由曲面和平面围成的是( )
A.球和圆锥 B.球和圆柱
C.圆锥和圆柱 D.圆柱和棱柱
3.下雨时,司机会打开雨刷器,雨刷器在运动时会形成一个扇面,这是因为( )
A.点动成线 B.线动成面
C.面动成体 D.面面相交形成线
B
C
4.如果一个多面体的一个面是多边形,其余各面都是有一个公共顶点的三角形,那么这个多面体叫做棱锥.如图是一个四棱柱和一个六棱锥,它们都有12条棱.下列棱柱中和九棱锥的棱数相等的是( )
练 习
B
A.五棱柱 B.六棱柱 C.七棱柱 D.八棱柱
练 习
5.如图所示的五棱柱,它的底面边长都是6 cm,侧棱长是8 cm,试回答下列问题:
(1)图中的五棱柱共有多少条棱?它们的长度分别是多少?
(2)图中的五棱柱共有多少个面?它们分别是什么形状?哪些面的形状和大小完全相同?
(3)求这个五棱柱的侧面积.
解:(1)五棱柱共有15条棱,侧面和上、下底面相交的棱长为6 cm,共10条;侧棱长均为8 cm,共5条;
(2)五棱柱共有7个面,底面都是五边形,侧面都是长方形;上、下底面的形状和大小完全相同,各个侧面的形状和大小完全相同;
(3)这个五棱柱的侧面积为6×8×5=240(cm2).
练 习
