人教版数学七年级上册2.2 第1课时 合并同类项课件 (11张)
文档属性
| 名称 | 人教版数学七年级上册2.2 第1课时 合并同类项课件 (11张) |  | |
| 格式 | ppt | ||
| 文件大小 | 982.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-03 09:07:32 | ||
图片预览




文档简介
第二章 整式的加减
2.2 整式的加减
第1课时 合并同类项
一、教学目标
1.理解同类项的概念,会判断同类项.
2.学会对同类项进行合并,并学会求值和应用.
3.体会分类和类比的数学思想.
重点
难点
合并同类项并求值.
正确合并同类项.
二、教学重难点
活动1 新课导入
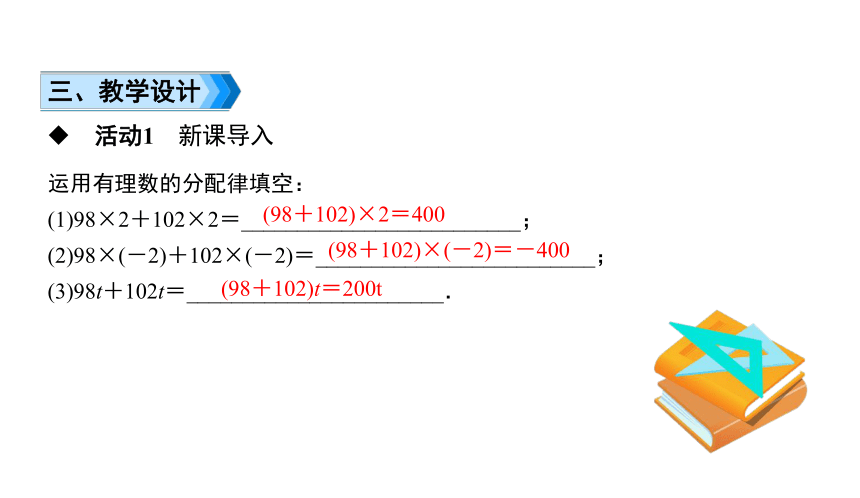
三、教学设计
运用有理数的分配律填空:
(1)98×2+102×2=_________________________;
(2)98×(-2)+102×(-2)=_________________________;
(3)98t+102t=_______________________.
(98+102)×2=400
(98+102)×(-2)=-400
(98+102)t=200t
活动2 探究新知
思考完成并交流展示.
提出问题:
(1)你能用含t的式子表示出从西宁到拉萨的铁路全长吗?
(2)类比数的运算,你能化简(1)中列出的式子吗?
(3)化简的依据是什么?
1.教材P62 探究及其上下的内容.
思考完成并交流展示.
2.教材P63 探究.
提出问题:
(1)探究中的式子有什么共同特点?
(2)能否用学过的运算律化简探究中的式子?
(3)通过化简你能从中得出什么规律?
活动3 知识归纳
1.所含______相同,并且相同字母的_______也相同的项叫做同类项,几个常数项也是__________.
字母
指数
同类项
2.把多项式中的_______合并成一项,叫做合并同类项.合并同类项后,所得项的系数是合并前各同类项的___________,且字母连同它的指数______.
同类项
系数的和
不变
活动4 例题与练习
例1 教材P64 例1.
例2 教材P64 例2.
例3 教材P65 例3.
例4 有这样一道题:“当a=0.35,b=-0.28时,求多项式7a3-6a3b+3a2b+3a3+6a3b-3a2b-10a3的值.”有位同学指出,题目中给出的条件a=0.35,b=-0.28是多余的,他的说法有道理吗?为什么?
解:有道理.理由如下:
∵7a3-6a3b+3a2b+3a3+6a3b-3a2b-10a3
=(7+3-10)a3+(-6+6)a3b+(3-3)a2b=0,
∴给出的条件a=0.35,b=-0.28是多余的.
1.教材P65 练习第1,2,3,4题.
练 习
2.下列各组式子中,是同类项的是 ( )
A.32y与-3xy2 B.3xy与-2yx
C.2x与2x2 D.5xy与5yz
B
3.如果多项式x2-7ab+b2+kab-1不含ab项,那么k的值为( )
A.0 B.7 C.1 D.不能确定
B
4.代数式4ambn-1与代数式-5a3b6的和只有一项,则m=____,n=____.
3
7
练 习
5.合并同类项:
(1)4a2+3b2+2ab-4a2-3b2;
解:原式=2ab;
(2)3x-2x2+5+3x2-2x-5;
解:原式=x2+x;
(3)a3+a2b+ab2-a2b-ab2-b3;
解:原式=a3-b3;
(4)6a2-5b2+2ab+5b2-6a2.
解:原式=2ab.
2.2 整式的加减
第1课时 合并同类项
一、教学目标
1.理解同类项的概念,会判断同类项.
2.学会对同类项进行合并,并学会求值和应用.
3.体会分类和类比的数学思想.
重点
难点
合并同类项并求值.
正确合并同类项.
二、教学重难点
活动1 新课导入
三、教学设计
运用有理数的分配律填空:
(1)98×2+102×2=_________________________;
(2)98×(-2)+102×(-2)=_________________________;
(3)98t+102t=_______________________.
(98+102)×2=400
(98+102)×(-2)=-400
(98+102)t=200t
活动2 探究新知
思考完成并交流展示.
提出问题:
(1)你能用含t的式子表示出从西宁到拉萨的铁路全长吗?
(2)类比数的运算,你能化简(1)中列出的式子吗?
(3)化简的依据是什么?
1.教材P62 探究及其上下的内容.
思考完成并交流展示.
2.教材P63 探究.
提出问题:
(1)探究中的式子有什么共同特点?
(2)能否用学过的运算律化简探究中的式子?
(3)通过化简你能从中得出什么规律?
活动3 知识归纳
1.所含______相同,并且相同字母的_______也相同的项叫做同类项,几个常数项也是__________.
字母
指数
同类项
2.把多项式中的_______合并成一项,叫做合并同类项.合并同类项后,所得项的系数是合并前各同类项的___________,且字母连同它的指数______.
同类项
系数的和
不变
活动4 例题与练习
例1 教材P64 例1.
例2 教材P64 例2.
例3 教材P65 例3.
例4 有这样一道题:“当a=0.35,b=-0.28时,求多项式7a3-6a3b+3a2b+3a3+6a3b-3a2b-10a3的值.”有位同学指出,题目中给出的条件a=0.35,b=-0.28是多余的,他的说法有道理吗?为什么?
解:有道理.理由如下:
∵7a3-6a3b+3a2b+3a3+6a3b-3a2b-10a3
=(7+3-10)a3+(-6+6)a3b+(3-3)a2b=0,
∴给出的条件a=0.35,b=-0.28是多余的.
1.教材P65 练习第1,2,3,4题.
练 习
2.下列各组式子中,是同类项的是 ( )
A.32y与-3xy2 B.3xy与-2yx
C.2x与2x2 D.5xy与5yz
B
3.如果多项式x2-7ab+b2+kab-1不含ab项,那么k的值为( )
A.0 B.7 C.1 D.不能确定
B
4.代数式4ambn-1与代数式-5a3b6的和只有一项,则m=____,n=____.
3
7
练 习
5.合并同类项:
(1)4a2+3b2+2ab-4a2-3b2;
解:原式=2ab;
(2)3x-2x2+5+3x2-2x-5;
解:原式=x2+x;
(3)a3+a2b+ab2-a2b-ab2-b3;
解:原式=a3-b3;
(4)6a2-5b2+2ab+5b2-6a2.
解:原式=2ab.
