人教版数学七年级上册4.3.3 余角和补角课件(12张)
文档属性
| 名称 | 人教版数学七年级上册4.3.3 余角和补角课件(12张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-30 12:27:17 | ||
图片预览





文档简介
第四章 几何图形初步
4.3 角
4.3.3 余角和补角
一、教学目标
1.了解余角、补角的概念,掌握余角和补角的性质.
2.了解方位角,能确定物体的具体方位.
重点
难点
余角和补角的性质.
方位角的应用.
二、教学重难点
活动1 新课导入
三、教学设计
1.已知∠1=61°,∠2=29°,那么∠1+∠2= .
2.已知∠1=62°,∠2=118°,那么∠1+∠2= .
90°
180°
活动2 探究新知
1.教材P137 内容.
提出问题:
(1)在一副三角尺中,同一块三角板中的两个锐角有什么关系?
(2)图4.3-14中,∠1+∠2=?
(3)∠1与∠2,∠3都互为补角,∠2与∠3的大小有什么关系?
(4)∠4与∠5,∠6都互为余角,∠5与∠6的大小有什么关系?
思考完成并交流展示.
2.教材P138 例4.
提出问题:
(1)方位角常以什么为基础,描述物体运动的方向?
(2)点B在点A的北偏东40°方向,则点A在点B的什么方向?
活动3 知识归纳
1.一般地,如果两个角的和等于 ,就说这两个角互为余角,即其中一个角是另一个角的 .类似地,如果两个角的和等于 ,就说这两个角互为补角,即其中一个角是另一个角的 .
2.同角(等角)的补角 ,同角(等角)的余角 .
3.方位角就是表示方向的角,一般以 、 方向为基准,描述物体运动的方向.记录时,通常要先写 或 ,再写
或 .
90°
余角
180°
补角
相等
相等
正北
正南
北偏
南偏
东
西
活动4 例题与练习
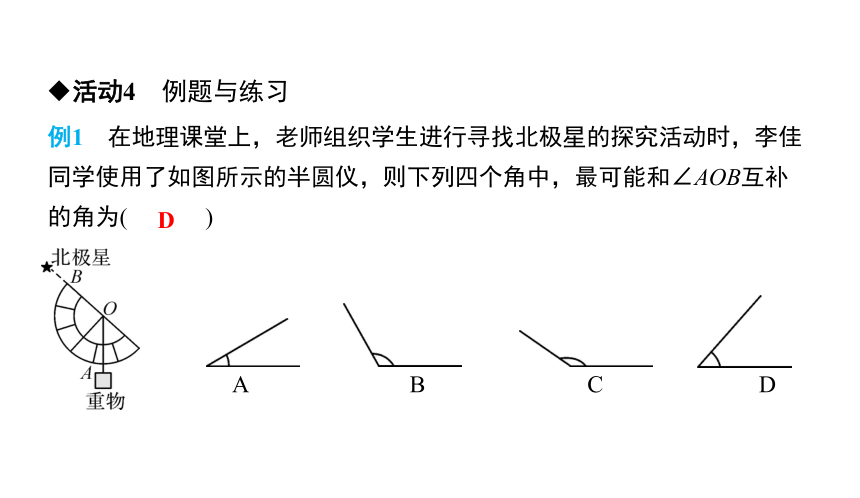
例1 在地理课堂上,老师组织学生进行寻找北极星的探究活动时,李佳同学使用了如图所示的半圆仪,则下列四个角中,最可能和∠AOB互补的角为( )
D
A B C D
例2 一个角的补角与这个角的余角的和是平角的 还多1°,求这个角.
解:设这个角为x,
则它的余角为(90°-x),补角为(180°-x).
由题意,得(90°-x+180°-x)- ×180°=1°,
解得x=67°.
答:这个角为67°.
例3 如图,A,O,B三点在同一条直线上,∠AOC=∠DOE=90°,图中共有几对相等的角?几对互余的角?几对互补的角?
解:相等的角有五对:∠1与∠3,∠2与∠4,∠AOC与∠COB,∠AOC与∠DOE,∠DOE与∠COB;
互余的角有四对:∠1与∠2,∠1与∠4,∠2与∠3,∠3与∠4;
互补的角有七对:∠1与∠DOB,∠4与∠AOE,∠AOC与∠COB,∠AOC与∠DOE,∠DOE与∠COB,∠3与∠DOB,∠2与∠AOE.
2.如果一个角是56°,那么下列说法中正确的是( )
A.它的余角是44° B.它的补角是44°
C.它的余角是124° D.它的补角是124°
3.如果一个角比它的余角大10°,那么这个角为( )
A.40° B.45° C.50° D.55°
1.教材P138~139 练习第1,2,3,4题.
练 习
C
D
4.如图,已知A,O,B三点在同一条直线上,∠AOC=∠BOC.若∠1=∠2,则图中互余的角共有( )
练 习
B
A.5对 B.4对 C.3对 D.2对
练 习
5. 如图,从点B看点A,点A所在的方向为( )
C
A.南偏东58° B.北偏西32°
C.南偏东32° D.北偏西58°
练 习
6.如图,已知∠AOC=2∠BOC,∠AOC的余角比∠BOC小30°.
(1)求∠AOB的度数;
(2)过点O作射线OD,使得∠AOC=4∠AOD,请你求出∠COD的度数.
解:(1)设∠BOC=x,则∠AOC=2x.依题意,得90°-2x=x-30°,解得x=40°,则∠AOB=∠BOC=40°;
(2)①当射线OD在∠AOC内部时,∠COD=60°;
②当射线OD在∠AOC外部时,∠COD=100°.
综上所述,∠COD的度数为60°或100°.
4.3 角
4.3.3 余角和补角
一、教学目标
1.了解余角、补角的概念,掌握余角和补角的性质.
2.了解方位角,能确定物体的具体方位.
重点
难点
余角和补角的性质.
方位角的应用.
二、教学重难点
活动1 新课导入
三、教学设计
1.已知∠1=61°,∠2=29°,那么∠1+∠2= .
2.已知∠1=62°,∠2=118°,那么∠1+∠2= .
90°
180°
活动2 探究新知
1.教材P137 内容.
提出问题:
(1)在一副三角尺中,同一块三角板中的两个锐角有什么关系?
(2)图4.3-14中,∠1+∠2=?
(3)∠1与∠2,∠3都互为补角,∠2与∠3的大小有什么关系?
(4)∠4与∠5,∠6都互为余角,∠5与∠6的大小有什么关系?
思考完成并交流展示.
2.教材P138 例4.
提出问题:
(1)方位角常以什么为基础,描述物体运动的方向?
(2)点B在点A的北偏东40°方向,则点A在点B的什么方向?
活动3 知识归纳
1.一般地,如果两个角的和等于 ,就说这两个角互为余角,即其中一个角是另一个角的 .类似地,如果两个角的和等于 ,就说这两个角互为补角,即其中一个角是另一个角的 .
2.同角(等角)的补角 ,同角(等角)的余角 .
3.方位角就是表示方向的角,一般以 、 方向为基准,描述物体运动的方向.记录时,通常要先写 或 ,再写
或 .
90°
余角
180°
补角
相等
相等
正北
正南
北偏
南偏
东
西
活动4 例题与练习
例1 在地理课堂上,老师组织学生进行寻找北极星的探究活动时,李佳同学使用了如图所示的半圆仪,则下列四个角中,最可能和∠AOB互补的角为( )
D
A B C D
例2 一个角的补角与这个角的余角的和是平角的 还多1°,求这个角.
解:设这个角为x,
则它的余角为(90°-x),补角为(180°-x).
由题意,得(90°-x+180°-x)- ×180°=1°,
解得x=67°.
答:这个角为67°.
例3 如图,A,O,B三点在同一条直线上,∠AOC=∠DOE=90°,图中共有几对相等的角?几对互余的角?几对互补的角?
解:相等的角有五对:∠1与∠3,∠2与∠4,∠AOC与∠COB,∠AOC与∠DOE,∠DOE与∠COB;
互余的角有四对:∠1与∠2,∠1与∠4,∠2与∠3,∠3与∠4;
互补的角有七对:∠1与∠DOB,∠4与∠AOE,∠AOC与∠COB,∠AOC与∠DOE,∠DOE与∠COB,∠3与∠DOB,∠2与∠AOE.
2.如果一个角是56°,那么下列说法中正确的是( )
A.它的余角是44° B.它的补角是44°
C.它的余角是124° D.它的补角是124°
3.如果一个角比它的余角大10°,那么这个角为( )
A.40° B.45° C.50° D.55°
1.教材P138~139 练习第1,2,3,4题.
练 习
C
D
4.如图,已知A,O,B三点在同一条直线上,∠AOC=∠BOC.若∠1=∠2,则图中互余的角共有( )
练 习
B
A.5对 B.4对 C.3对 D.2对
练 习
5. 如图,从点B看点A,点A所在的方向为( )
C
A.南偏东58° B.北偏西32°
C.南偏东32° D.北偏西58°
练 习
6.如图,已知∠AOC=2∠BOC,∠AOC的余角比∠BOC小30°.
(1)求∠AOB的度数;
(2)过点O作射线OD,使得∠AOC=4∠AOD,请你求出∠COD的度数.
解:(1)设∠BOC=x,则∠AOC=2x.依题意,得90°-2x=x-30°,解得x=40°,则∠AOB=∠BOC=40°;
(2)①当射线OD在∠AOC内部时,∠COD=60°;
②当射线OD在∠AOC外部时,∠COD=100°.
综上所述,∠COD的度数为60°或100°.
