五年级上册数学教案-5.1 平行四边形的面积青岛版
文档属性
| 名称 | 五年级上册数学教案-5.1 平行四边形的面积青岛版 |

|
|
| 格式 | doc | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-01 00:00:00 | ||
图片预览

文档简介
平行四边形的面积
几点尝试:
1、学生的学习经验,我们不仅要敢于暴露,而且要尽早暴露。因为暴露得越早,就会越快地引起学生的关注,激起学生的探究欲望,学生探究的时间、空间也会越充分,教学的针对性就更强。
2、渗透合情推理的思想:由一个例子推导出公式是缺乏科学性的,通过多个不同情况下的实例推断出同一个结论,是比较符合小学阶段所能够理解的合情推理思想的。
3、ICT教学法的运用:为了避免(或者说是减少)“因为要用信息技术而用信息技术”对备课的影响,本节课主要在
前测、后测部分使用了Forclass的统计功能;
图形第一次转化部分借助几何画板和Forclass的投票功能;
小组活动部分借助ppt的图片功能;
图形转化过程中的等量关系则嵌入课上翻转。
而在练习题部分,考虑到纸质版课本引入会导致课本和平板交错、桌面凌乱,因此继续让学生在平板完成。
三维目标(教学目标,包含学生目标):
知识与技能:(1)学生通过大胆猜测、师生探讨“合情推理”出平行四边形面积计算公式; (2)能正确计算平行四边形的面积。
过程与方法:让学生经历尝试探索平行四边形面积公式的推导过程,通过操作、观察、比较、推理和概括能力,发展学生的空间观念,渗透转化的思想方法。
情感态度与价值观:感受数学源于生活,生活需要数学;带学生体会尝试学习和信息技术介入的快感;培养学生的分析、综合、抽象、概括和解决实际问题的能力,增强学生学习数学的积极性;感受学习数学的快乐。
教学重难点:
教学重点:理解公式并正确计算平行四边形的面积。
教学难点:理解平行四边形面积公式的“合情推理”过程。
教学过程:
一、课堂前测
师:大家有参加过“香洲义工”活动吗?(举手示意)
师:哇,居然有这么多都参加过了呀!表扬乐于奉献社会的小朋友们!王老师和李老师也参加了“香洲义工”活动。大家请看:
师:你认为哪位老师做的比较多呢?
师:活动开始,请大家打开平板,完成投票。
师:活动结束,请收起平板。(查看投票结果,及时提醒那些没有来得及投票的同学)
【课后反馈:选择了第二第三个的学生人数较多,部分学生纯属猜测,但这也是探究学习的伊始】
二、新知探索
1、开门见山,抛出问题
师:有谁能够告诉大家,比较谁做的多,关键是比较什么?(预设:草坪的面积)看的真准!左边草坪的面积会求吗?(举手示意,及时板书长方形的面积公式)
师:右边草坪是一个……(平行四边形),那平行四边形的面积又该怎么计算呢?这就是我们这节课要一起学习的内容(提示板书上的课题)。
师:大家知道吗?很多新知识都是从尝试中获得的。所以,在我们学习这个平行四边形的面积公式前,老师请大家先尝试去计算这个平行四边形的面积。
2、学会尝试,探讨问题
师:活动开始,请大家打开平板,在相应的地方列式计算。
3分钟后教师组织学生反馈。(打开计时器。)
预计:
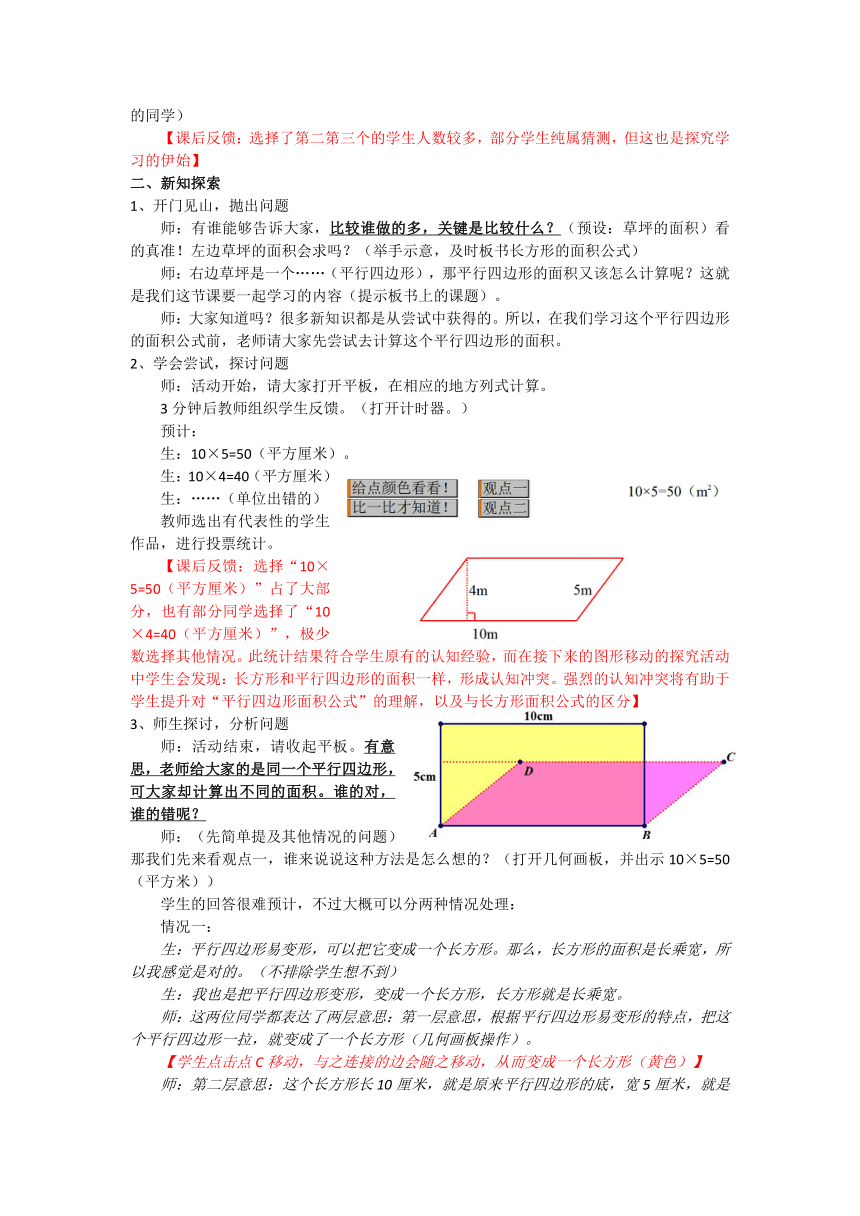
生:10×5=50(平方厘米)。
生:10×4=40(平方厘米)
生:……(单位出错的)
教师选出有代表性的学生作品,进行投票统计。
【课后反馈:选择“10×5=50(平方厘米)”占了大部分,也有部分同学选择了“10×4=40(平方厘米)”,极少数选择其他情况。此统计结果符合学生原有的认知经验,而在接下来的图形移动的探究活动中学生会发现:长方形和平行四边形的面积一样,形成认知冲突。强烈的认知冲突将有助于学生提升对“平行四边形面积公式”的理解,以及与长方形面积公式的区分】
3、师生探讨,分析问题
师:活动结束,请收起平板。有意思,老师给大家的是同一个平行四边形,可大家却计算出不同的面积。谁的对,谁的错呢?
师:(先简单提及其他情况的问题)那我们先来看观点一,谁来说说这种方法是怎么想的?(打开几何画板,并出示10×5=50(平方米))
学生的回答很难预计,不过大概可以分两种情况处理:
情况一:
生:平行四边形易变形,可以把它变成一个长方形。那么,长方形的面积是长乘宽,所以我感觉是对的。(不排除学生想不到)
生:我也是把平行四边形变形,变成一个长方形,长方形就是长乘宽。
师:这两位同学都表达了两层意思:第一层意思,根据平行四边形易变形的特点,把这个平行四边形一拉,就变成了一个长方形(几何画板操作)。
【学生点击点C移动,与之连接的边会随之移动,从而变成一个长方形(黄色)】
师:第二层意思:这个长方形长10厘米,就是原来平行四边形的底,宽5厘米,就是原来平行四边形的邻边。长方形的面积等于长乘宽,所以,平行四边形的面积等于底乘邻边。听他们这么一说,感觉好像是有点道理?
师:都赞同吗?有不同意见的?
生:拉动,平行四边形在变,高在变,面积也在变。
师:我们这样一拉,形状发生了变化,【教师移动点C,实现几何画板上的动画展示】这位同学认为面积也发生变化了,(面向全班)你们也认为变了吗? 面积变了吗?有没有办法让我们看得更加清楚面积的变化?
生:最简单的方法就是把突出来的这个三角形切出来,移到左边去,就变成一个小长方形了,很明显,黄色的长方形对于紫色的。(使用几何画板展示。如果学生想不到,可以考虑出示长方形作为提醒)
师:大家赞同吗?真有想法!把突出来的部分切割,然后补到左边,刚好形成一 个长方形。从图中可以明显的看出,平行四边形的面积小于长方形的面积。也就是观点一的方法算出来的面积偏大了。
情况二:
生:长方形是两条边相乘,我想平行四边形也应是。
师:哦!那老师可不可以理解成你也是在求长为10m,宽为5m的长方形的面积?(几何画板出示长方形)
师:也就是说这两个图形的面积应该是……相等的。大家觉得是这个理吗?
师:那这两个图形到底相不相等呢?有什么办法可以比较出来?(预设:重叠)
师:这位同学真聪明,大家请看(几何画板操作):多出了一块,怎么办?(预设:把多出来的切出来,补到右边去)
师:好,李老师帮你把它切成两块,给点颜色。请你上来示范一下怎么补?(与 情况一殊路同归)
师:大家有什么发现?(预设:长方形的面积比平行四边形的大)也就是说刚才这种算法是错误的。所以,我们计算平行四边形的面积的时候不能用相邻的两条边相乘。
师:我们再来看看观点二的做法(几何画板上板书:10×4=40(平方米))吗?
生:……(预设学生会借助刚才的割补讲解,不然,则教师在学生将不明白的时候进行引导)
师:说得真好!这么一割补,就把平行四边形的面积转化成了长方形的面积(板书:箭头,朝上)
4、整理总结,解决问题
师:那这个长方形的长是多少?宽呢?(引导学生指出平行四边形和长方形之间的等量关系)也就是长方形的长就等于原来平行四边形的底,宽就等于高。
师:平行四边形的公式就可以写成:底×高。
三、深入探究
师:李老师发现,咱们二班的孩子不仅看得清楚,还想得明白!
师:不过大家有没有发现,我们之所以可以推导出这条公式,关键在于把平行四边形转成长方形。那是不是所有的平行四边形都可以转化成长方形呢?
师:(打开ppt)李老师这里给出了各种不同情况的平行四边形,请大家帮忙验证。活动开始,打开平板。
师:(出示探讨内容,小组交流)
探讨内容:
1、和小组同学对比一下,是不是七幅图都可以实现转化?2、哪一幅不可以,为什么?
3、你能得到什么结论?
小组活动——验证
师:时间到了。请大家根据你的完成情况,选出可以转化的平行四边形(多选题——技术缺失:没有能够实现多个选项的投票功能,此处通过多选题实现数据统计)
师:大部分同学都认为1到6的平行四边形都可以转化,第七次尝试中的两个平行四边不可以。我们一起看看是怎么回事(ppt),不能转化的原因是……(没有沿着高割补)
师:所以我们不能说这两个平行四边形并不是不能转化成长方形,而只是没有沿着高切割。所以,我们可以得到一个什么结论呢?(切换回Forclass活动界面,所有的平行四边形都可以转化成长方形)也就是说所有的平行四边形的面积都可以用底×高来计算。
师:真棒!平行四边形的面积公式我们知道了,那图形转化过程中的等量关系大家是否也都清楚了呢?请大家观察视频,然后解决后面的问题。
四、课堂后测(知识巩固)
检测一:填空题——两者之间的等量关系
检测二:应用题——公式的基本运用
检测三:计算题——强调底×高中的高指的是“底上高” 反馈:
检测四:思考题——等底等高的两个平行四边形面积相等 示范(几何画板):
检测五:计算题——逆向思维:知道面积求高(时间不够则跳过)
检测六:选择题——与前测形成对比,反馈学生学习情况
五、板书设计
平行四边形的面积
长方形的面积=长×宽
平行四边形的面积=底×高
几点尝试:
1、学生的学习经验,我们不仅要敢于暴露,而且要尽早暴露。因为暴露得越早,就会越快地引起学生的关注,激起学生的探究欲望,学生探究的时间、空间也会越充分,教学的针对性就更强。
2、渗透合情推理的思想:由一个例子推导出公式是缺乏科学性的,通过多个不同情况下的实例推断出同一个结论,是比较符合小学阶段所能够理解的合情推理思想的。
3、ICT教学法的运用:为了避免(或者说是减少)“因为要用信息技术而用信息技术”对备课的影响,本节课主要在
前测、后测部分使用了Forclass的统计功能;
图形第一次转化部分借助几何画板和Forclass的投票功能;
小组活动部分借助ppt的图片功能;
图形转化过程中的等量关系则嵌入课上翻转。
而在练习题部分,考虑到纸质版课本引入会导致课本和平板交错、桌面凌乱,因此继续让学生在平板完成。
三维目标(教学目标,包含学生目标):
知识与技能:(1)学生通过大胆猜测、师生探讨“合情推理”出平行四边形面积计算公式; (2)能正确计算平行四边形的面积。
过程与方法:让学生经历尝试探索平行四边形面积公式的推导过程,通过操作、观察、比较、推理和概括能力,发展学生的空间观念,渗透转化的思想方法。
情感态度与价值观:感受数学源于生活,生活需要数学;带学生体会尝试学习和信息技术介入的快感;培养学生的分析、综合、抽象、概括和解决实际问题的能力,增强学生学习数学的积极性;感受学习数学的快乐。
教学重难点:
教学重点:理解公式并正确计算平行四边形的面积。
教学难点:理解平行四边形面积公式的“合情推理”过程。
教学过程:
一、课堂前测
师:大家有参加过“香洲义工”活动吗?(举手示意)
师:哇,居然有这么多都参加过了呀!表扬乐于奉献社会的小朋友们!王老师和李老师也参加了“香洲义工”活动。大家请看:
师:你认为哪位老师做的比较多呢?
师:活动开始,请大家打开平板,完成投票。
师:活动结束,请收起平板。(查看投票结果,及时提醒那些没有来得及投票的同学)
【课后反馈:选择了第二第三个的学生人数较多,部分学生纯属猜测,但这也是探究学习的伊始】
二、新知探索
1、开门见山,抛出问题
师:有谁能够告诉大家,比较谁做的多,关键是比较什么?(预设:草坪的面积)看的真准!左边草坪的面积会求吗?(举手示意,及时板书长方形的面积公式)
师:右边草坪是一个……(平行四边形),那平行四边形的面积又该怎么计算呢?这就是我们这节课要一起学习的内容(提示板书上的课题)。
师:大家知道吗?很多新知识都是从尝试中获得的。所以,在我们学习这个平行四边形的面积公式前,老师请大家先尝试去计算这个平行四边形的面积。
2、学会尝试,探讨问题
师:活动开始,请大家打开平板,在相应的地方列式计算。
3分钟后教师组织学生反馈。(打开计时器。)
预计:
生:10×5=50(平方厘米)。
生:10×4=40(平方厘米)
生:……(单位出错的)
教师选出有代表性的学生作品,进行投票统计。
【课后反馈:选择“10×5=50(平方厘米)”占了大部分,也有部分同学选择了“10×4=40(平方厘米)”,极少数选择其他情况。此统计结果符合学生原有的认知经验,而在接下来的图形移动的探究活动中学生会发现:长方形和平行四边形的面积一样,形成认知冲突。强烈的认知冲突将有助于学生提升对“平行四边形面积公式”的理解,以及与长方形面积公式的区分】
3、师生探讨,分析问题
师:活动结束,请收起平板。有意思,老师给大家的是同一个平行四边形,可大家却计算出不同的面积。谁的对,谁的错呢?
师:(先简单提及其他情况的问题)那我们先来看观点一,谁来说说这种方法是怎么想的?(打开几何画板,并出示10×5=50(平方米))
学生的回答很难预计,不过大概可以分两种情况处理:
情况一:
生:平行四边形易变形,可以把它变成一个长方形。那么,长方形的面积是长乘宽,所以我感觉是对的。(不排除学生想不到)
生:我也是把平行四边形变形,变成一个长方形,长方形就是长乘宽。
师:这两位同学都表达了两层意思:第一层意思,根据平行四边形易变形的特点,把这个平行四边形一拉,就变成了一个长方形(几何画板操作)。
【学生点击点C移动,与之连接的边会随之移动,从而变成一个长方形(黄色)】
师:第二层意思:这个长方形长10厘米,就是原来平行四边形的底,宽5厘米,就是原来平行四边形的邻边。长方形的面积等于长乘宽,所以,平行四边形的面积等于底乘邻边。听他们这么一说,感觉好像是有点道理?
师:都赞同吗?有不同意见的?
生:拉动,平行四边形在变,高在变,面积也在变。
师:我们这样一拉,形状发生了变化,【教师移动点C,实现几何画板上的动画展示】这位同学认为面积也发生变化了,(面向全班)你们也认为变了吗? 面积变了吗?有没有办法让我们看得更加清楚面积的变化?
生:最简单的方法就是把突出来的这个三角形切出来,移到左边去,就变成一个小长方形了,很明显,黄色的长方形对于紫色的。(使用几何画板展示。如果学生想不到,可以考虑出示长方形作为提醒)
师:大家赞同吗?真有想法!把突出来的部分切割,然后补到左边,刚好形成一 个长方形。从图中可以明显的看出,平行四边形的面积小于长方形的面积。也就是观点一的方法算出来的面积偏大了。
情况二:
生:长方形是两条边相乘,我想平行四边形也应是。
师:哦!那老师可不可以理解成你也是在求长为10m,宽为5m的长方形的面积?(几何画板出示长方形)
师:也就是说这两个图形的面积应该是……相等的。大家觉得是这个理吗?
师:那这两个图形到底相不相等呢?有什么办法可以比较出来?(预设:重叠)
师:这位同学真聪明,大家请看(几何画板操作):多出了一块,怎么办?(预设:把多出来的切出来,补到右边去)
师:好,李老师帮你把它切成两块,给点颜色。请你上来示范一下怎么补?(与 情况一殊路同归)
师:大家有什么发现?(预设:长方形的面积比平行四边形的大)也就是说刚才这种算法是错误的。所以,我们计算平行四边形的面积的时候不能用相邻的两条边相乘。
师:我们再来看看观点二的做法(几何画板上板书:10×4=40(平方米))吗?
生:……(预设学生会借助刚才的割补讲解,不然,则教师在学生将不明白的时候进行引导)
师:说得真好!这么一割补,就把平行四边形的面积转化成了长方形的面积(板书:箭头,朝上)
4、整理总结,解决问题
师:那这个长方形的长是多少?宽呢?(引导学生指出平行四边形和长方形之间的等量关系)也就是长方形的长就等于原来平行四边形的底,宽就等于高。
师:平行四边形的公式就可以写成:底×高。
三、深入探究
师:李老师发现,咱们二班的孩子不仅看得清楚,还想得明白!
师:不过大家有没有发现,我们之所以可以推导出这条公式,关键在于把平行四边形转成长方形。那是不是所有的平行四边形都可以转化成长方形呢?
师:(打开ppt)李老师这里给出了各种不同情况的平行四边形,请大家帮忙验证。活动开始,打开平板。
师:(出示探讨内容,小组交流)
探讨内容:
1、和小组同学对比一下,是不是七幅图都可以实现转化?2、哪一幅不可以,为什么?
3、你能得到什么结论?
小组活动——验证
师:时间到了。请大家根据你的完成情况,选出可以转化的平行四边形(多选题——技术缺失:没有能够实现多个选项的投票功能,此处通过多选题实现数据统计)
师:大部分同学都认为1到6的平行四边形都可以转化,第七次尝试中的两个平行四边不可以。我们一起看看是怎么回事(ppt),不能转化的原因是……(没有沿着高割补)
师:所以我们不能说这两个平行四边形并不是不能转化成长方形,而只是没有沿着高切割。所以,我们可以得到一个什么结论呢?(切换回Forclass活动界面,所有的平行四边形都可以转化成长方形)也就是说所有的平行四边形的面积都可以用底×高来计算。
师:真棒!平行四边形的面积公式我们知道了,那图形转化过程中的等量关系大家是否也都清楚了呢?请大家观察视频,然后解决后面的问题。
四、课堂后测(知识巩固)
检测一:填空题——两者之间的等量关系
检测二:应用题——公式的基本运用
检测三:计算题——强调底×高中的高指的是“底上高” 反馈:
检测四:思考题——等底等高的两个平行四边形面积相等 示范(几何画板):
检测五:计算题——逆向思维:知道面积求高(时间不够则跳过)
检测六:选择题——与前测形成对比,反馈学生学习情况
五、板书设计
平行四边形的面积
长方形的面积=长×宽
平行四边形的面积=底×高
