一元二次方程（1）

(共14张PPT)

学习目标
1.理解一元二次方程的概念，
根据一元二 次方程的一般
式，确定各项系数
2.灵活应用一元二次方程概念
解决有关问题

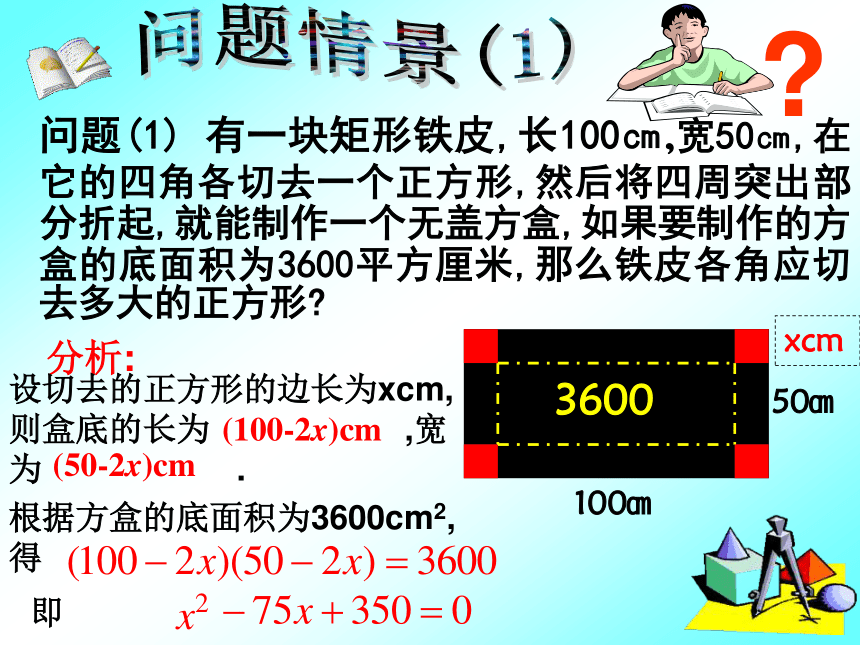
问题(1) 有一块矩形铁皮,长100㎝,宽50㎝,在它的四角各切去一个正方形,然后将四周突出部分折起,就能制作一个无盖方盒,如果要制作的方盒的底面积为3600平方厘米,那么铁皮各角应切去多大的正方形
100㎝
50㎝
xcm
3600
分析:
设切去的正方形的边长为xcm,则盒底的长为 ,宽为 .
(100-2x)cm
(50-2x)cm
根据方盒的底面积为3600cm2,得
即

问题(2) 要组织一次排球邀请赛,参赛的每两队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应邀请多少个队参加比赛
分析:
全部比赛共
4×7=28场
设应邀请x个队参赛,每个队要与其他 个队各赛1场,
由于甲队对乙队的比赛和乙队对甲队的比赛
是同一场比赛,所以全部比赛共 场.
即
(x-1)
这两个方程都不是一元一次方程.那么这两个方程与一元一次方程的区别在哪里？它们有什么共同特点呢？
特点:
①都是整式方程;
②只含一个未知数;
③未知数的最高次数是2.
一元二次方程的概念
像这样的等号两边都是整式, 只含有一个未知数(一元)，并且未知数的最高次数是2(二次)的方程叫做一元二次方程(quadratic equation in one unknown)
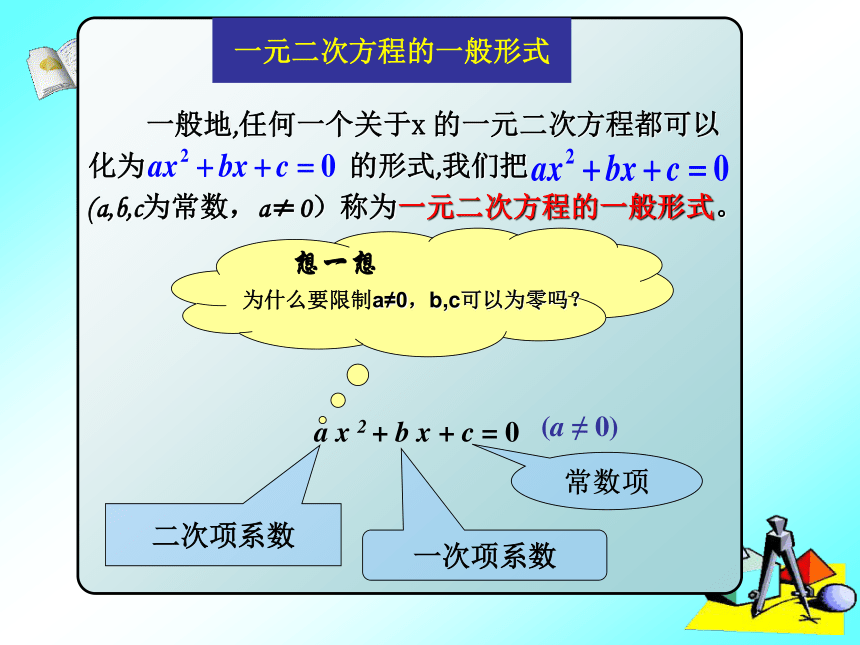
一元二次方程的一般形式
一般地,任何一个关于x 的一元二次方程都可以
化为 的形式,我们把
(a,b,c为常数，a≠0）称为一元二次方程的一般形式。
为什么要限制a≠0，b,c可以为零吗？
想一想
a x 2 + b x + c = 0
(a ≠ 0)
二次项系数
一次项系数
常数项

尝试应用
[1]判断下列方程是否为一元二次方程？
（1）
（2）
（3）
3
5
2
3
-
=
+
y
x

例题讲解
[2] 将下列方程化为一般形式，并分别指出它们的二次项、一次项和常数项及它们的系数：
二次项、二次项系数、一次项、一次项系数、常数项都是包括符号的
尝试应用
解:
3 x 2-8 x -10=0
二次项系数是3、一次项系数是-8、
常数项是-10
展示交流
[1] 将下列方程化为一元二次方程的一般形式，并分别指出其中的二次项系数、一次项系数和常数项：
(1) 5x2-1=4x
(2) 4x2=81
(3) 4x(x+2)=25
(4) (3x-2)(x+1)=8x-3
展示交流
例题讲解
[2]方程（2a-4）x2 -2bx+a=0, 在什么条件下此方程为一元二次方程？在什么条件下此方程为一元一次方程？
解：当a≠2时是一元二次方程；
当a＝2，b≠0时是一元一次方程；
展示交流
1.下列方程中,无论a为何值,总是关于x的一元二次方程的是( )
A.(2x-1)(x2+3)=2x2-a B.ax2+2x+4=0
C.ax2+x=x2-1 D.(a2+1)x2=0
2.当m为何值时,方程
是关于x的一元二次方程.
D
1.一元二次方程的概念
只含有一个未知数，并且未知数的最高次数是2的整式方程叫做一元二次方程。
2、一元二次方程的一般形式
(a,b,c为常数，a≠0)
谢谢,再见!
习题22.1 1.（2） （4） （6）
2.