新人教七年数学下 5.1.1相交线
文档属性
| 名称 | 新人教七年数学下 5.1.1相交线 |

|
|
| 格式 | rar | ||
| 文件大小 | 503.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-09-19 00:00:00 | ||
图片预览



文档简介
(共20张PPT)
大桥上的钢梁和钢索
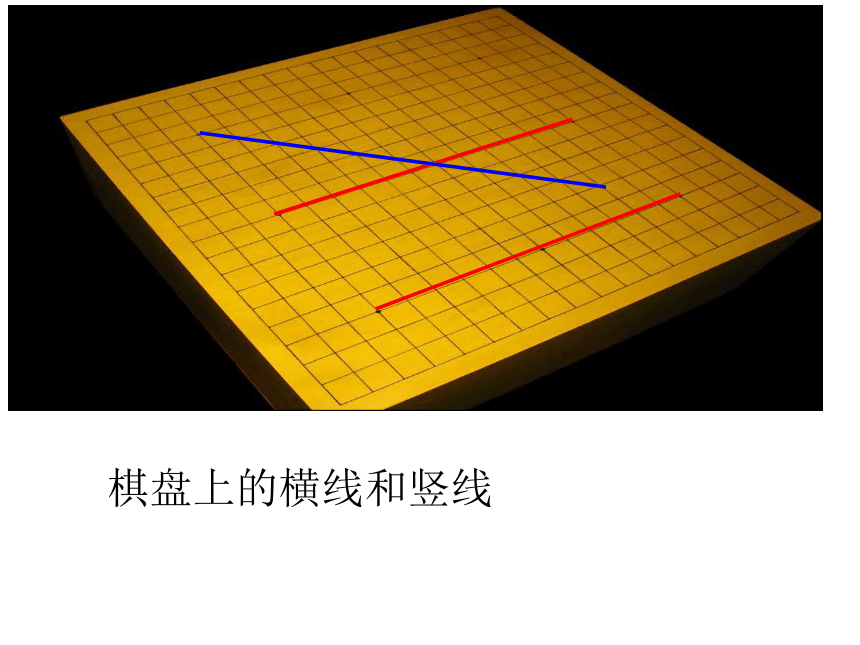
棋盘上的横线和竖线
第五章相交线与平行线
5.1.1 相 交 线
问题
(1)看见一把张开的剪刀,你能联想出什么样的几何图形?
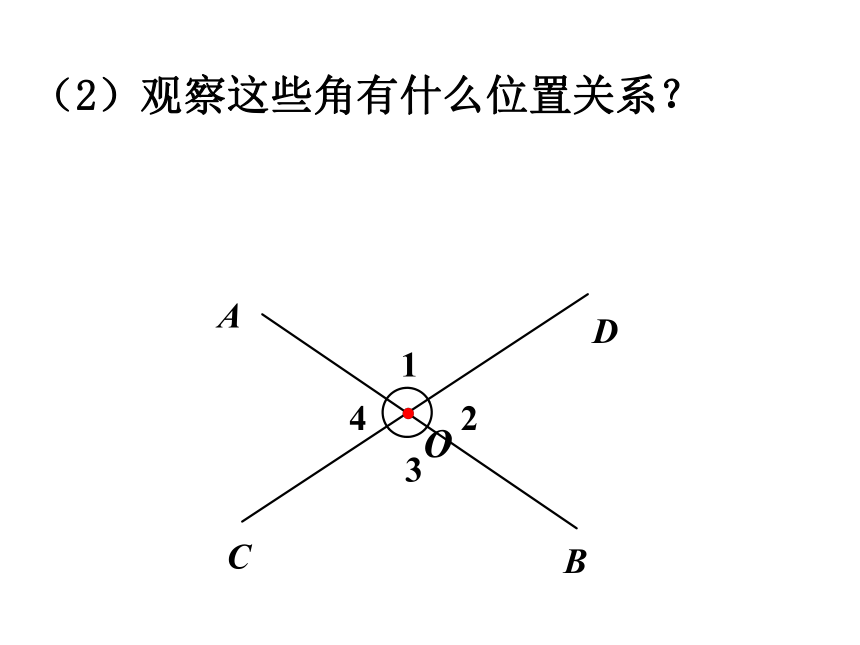
(2)观察这些角有什么位置关系?
O
A
B
C
D
)
(
1
3
4
2
)
(
O
A
B
C
D
)
(
1
3
4
2
)
(
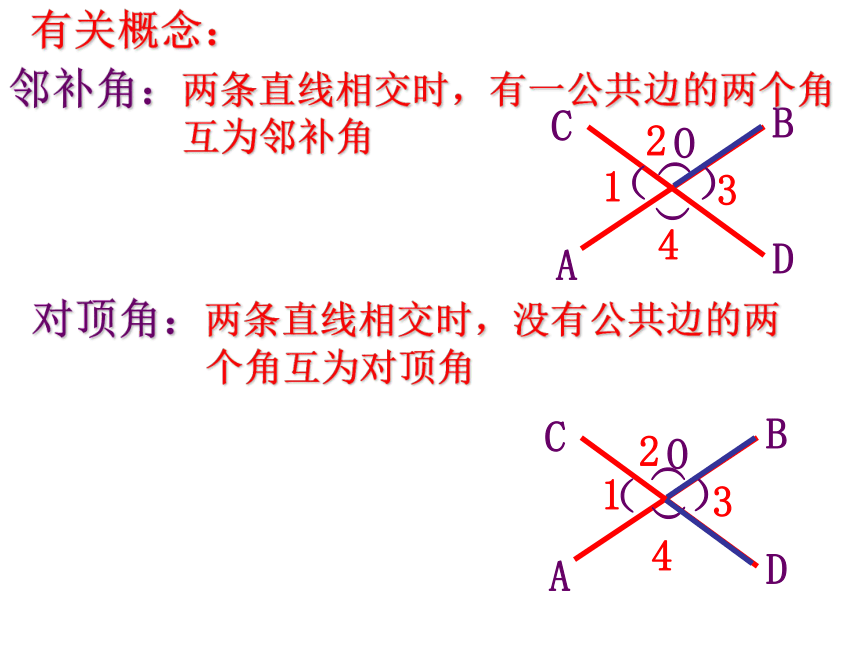
有关概念:
邻补角:两条直线相交时,有一公共边的两个角
互为邻补角
对顶角:两条直线相交时,没有公共边的两
个角互为对顶角
1
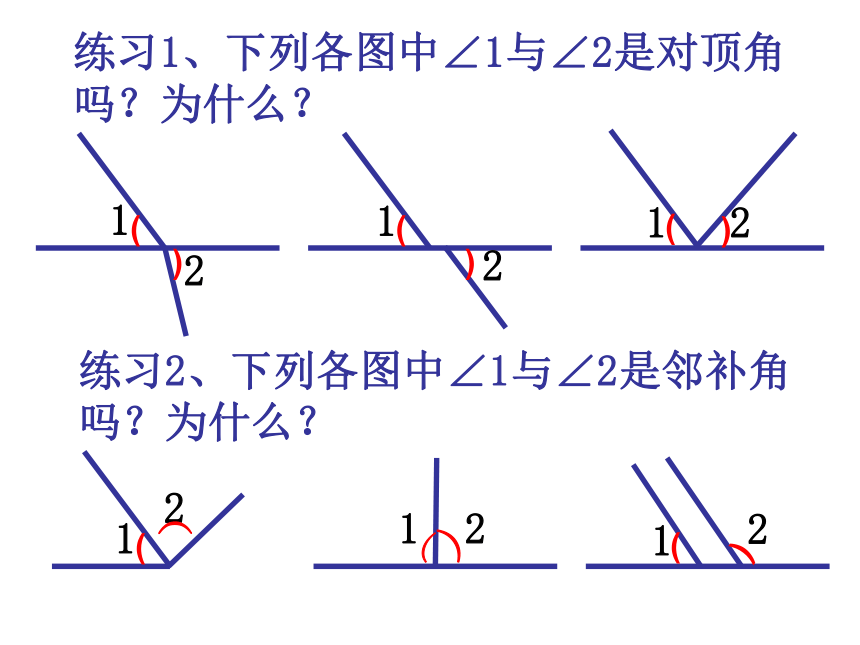
练习1、下列各图中∠1与∠2是对顶角吗?为什么?
2
1
2
1
2
)
(
(
(
)
)
1
练习2、下列各图中∠1与∠2是邻补角吗?为什么?
2
1
2
1
2
)
(
(
(
)
(
问题
找出图中∠AOC的对顶角及邻补角,
∠AOE呢?若没有请画出.
对顶角相等.
对顶角的性质:
O
A
B
C
D
)
(
1
3
4
2
)
(
为什么
已知:直线AB与CD相交于O点(如图),说明∠1=∠3、 ∠2=∠4的理由
解:∵直线AB与CD相交于O点,
∴∠1+∠2=180°、 ∠2+∠3=180°
∴∠1=∠3
同理可得:∠2=∠4
(
a
b
)
(
1
3
4
2
)
例1、如图,直线a、b相交,∠1=40°,求 ∠2、∠3、∠ 4的度数。
问题
(1)直线a、b相交,∠1=35°,
求∠2、∠3、∠4的度数.
(2)∠1等于90°时,
∠2、∠3、∠4等于多少度?
(
a
b
)
(
1
3
4
2
)
例1、如图,直线a、b相交,
变式1:若∠2是∠1的3倍,求∠3的度数?
变式2:若∠2-∠1=400, 求∠4的度数?
解:∵∠DOB=∠ ,( )
=80°(已知)
∴∠DOB= °(等量代换)
又∵∠1=30°( )
∴∠2=∠ -∠ = - = °
1、一个角的对顶角有 个,邻补角最多有
个,而补角则可以有 个。
3、如图,直线AB、CD相交于O,∠AOC=80°∠1=30°;求∠2的度数.
A
C
B
D
E
1
一
两
无数
AOC
∠AOC
DOB
1
80°
30°
50
对顶角相等
已知
二、 填空
80
2、右图中∠AOC的对顶角是 ,
邻补角是 .
∠DOB
∠AOD和∠COB
2
)
)
O
归纳小结
角的
名称 特 征 性 质 相 同 点 不 同 点
对
顶
角
邻
补
角
对顶
角相
等
邻补
角互
补
②有公共顶点;
③没有公共边
①两条直线相交形成的角;
①两条直线相交而成;
②有公共顶点;
③有一条公共边
①都是两条直线相交而成的角;
③都是成对出现的
②都有一个公共顶点;
②两直线相交时,
对顶角只有两对
邻补角有四对
①有无公共边
大桥上的钢梁和钢索
棋盘上的横线和竖线
第五章相交线与平行线
5.1.1 相 交 线
问题
(1)看见一把张开的剪刀,你能联想出什么样的几何图形?
(2)观察这些角有什么位置关系?
O
A
B
C
D
)
(
1
3
4
2
)
(
O
A
B
C
D
)
(
1
3
4
2
)
(
有关概念:
邻补角:两条直线相交时,有一公共边的两个角
互为邻补角
对顶角:两条直线相交时,没有公共边的两
个角互为对顶角
1
练习1、下列各图中∠1与∠2是对顶角吗?为什么?
2
1
2
1
2
)
(
(
(
)
)
1
练习2、下列各图中∠1与∠2是邻补角吗?为什么?
2
1
2
1
2
)
(
(
(
)
(
问题
找出图中∠AOC的对顶角及邻补角,
∠AOE呢?若没有请画出.
对顶角相等.
对顶角的性质:
O
A
B
C
D
)
(
1
3
4
2
)
(
为什么
已知:直线AB与CD相交于O点(如图),说明∠1=∠3、 ∠2=∠4的理由
解:∵直线AB与CD相交于O点,
∴∠1+∠2=180°、 ∠2+∠3=180°
∴∠1=∠3
同理可得:∠2=∠4
(
a
b
)
(
1
3
4
2
)
例1、如图,直线a、b相交,∠1=40°,求 ∠2、∠3、∠ 4的度数。
问题
(1)直线a、b相交,∠1=35°,
求∠2、∠3、∠4的度数.
(2)∠1等于90°时,
∠2、∠3、∠4等于多少度?
(
a
b
)
(
1
3
4
2
)
例1、如图,直线a、b相交,
变式1:若∠2是∠1的3倍,求∠3的度数?
变式2:若∠2-∠1=400, 求∠4的度数?
解:∵∠DOB=∠ ,( )
=80°(已知)
∴∠DOB= °(等量代换)
又∵∠1=30°( )
∴∠2=∠ -∠ = - = °
1、一个角的对顶角有 个,邻补角最多有
个,而补角则可以有 个。
3、如图,直线AB、CD相交于O,∠AOC=80°∠1=30°;求∠2的度数.
A
C
B
D
E
1
一
两
无数
AOC
∠AOC
DOB
1
80°
30°
50
对顶角相等
已知
二、 填空
80
2、右图中∠AOC的对顶角是 ,
邻补角是 .
∠DOB
∠AOD和∠COB
2
)
)
O
归纳小结
角的
名称 特 征 性 质 相 同 点 不 同 点
对
顶
角
邻
补
角
对顶
角相
等
邻补
角互
补
②有公共顶点;
③没有公共边
①两条直线相交形成的角;
①两条直线相交而成;
②有公共顶点;
③有一条公共边
①都是两条直线相交而成的角;
③都是成对出现的
②都有一个公共顶点;
②两直线相交时,
对顶角只有两对
邻补角有四对
①有无公共边
