人教版 九年级 上册 24.1圆的有关性质 同步练习(Word版 含解析)
文档属性
| 名称 | 人教版 九年级 上册 24.1圆的有关性质 同步练习(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 325.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-01 10:16:10 | ||
图片预览


文档简介
圆的有关性质同步练习
一、选择题
下列命题正确的有平分弦所对的两条弧的直线必垂直于弦
垂直于弦的直线平分弦
平分弦的直线必平分弦所对的两条弧
与直径不垂直的弦不能被该直径平分
平分弦的直径必平分弦所对的两条弧.
A.
1个
B.
2个
C.
3个
D.
4个
如图,已知A,B,C,D,E均在上,且AC为直径,则
A.
B.
C.
D.
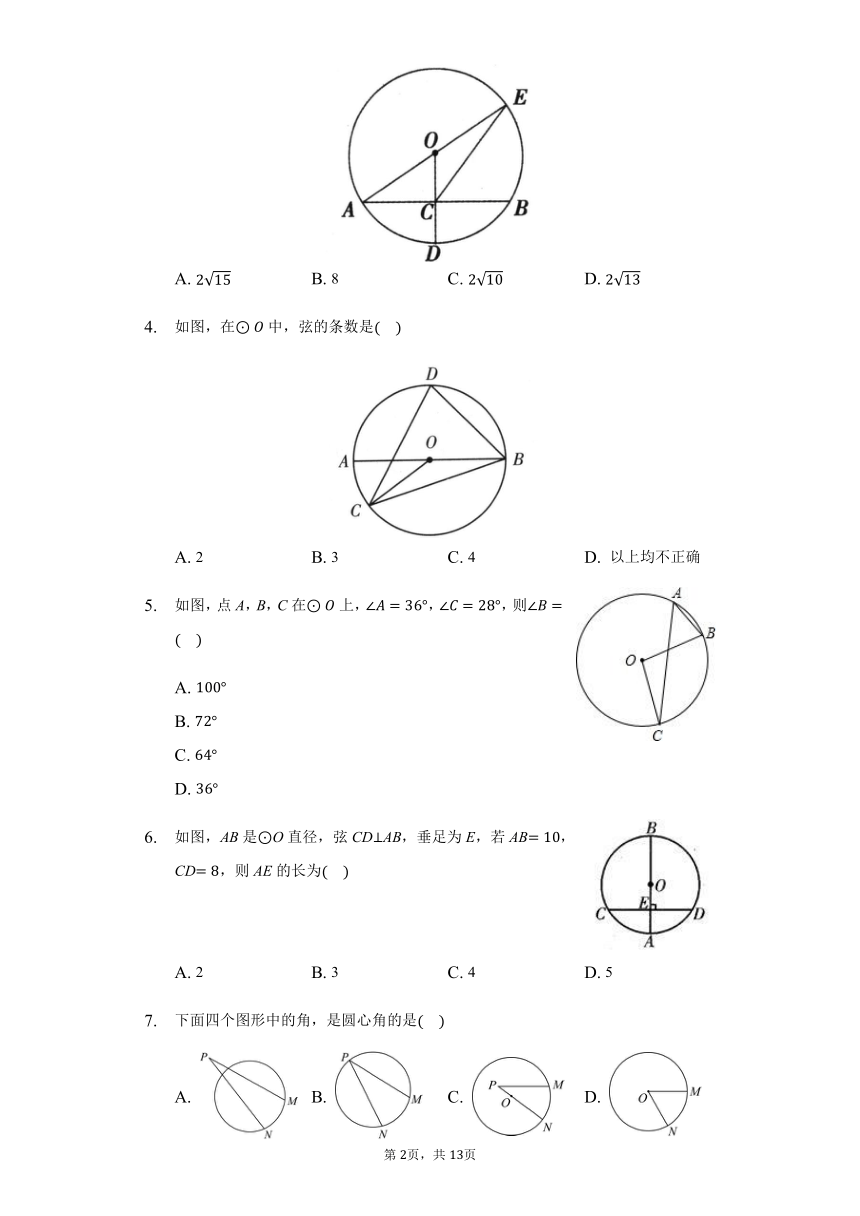
如图,在中,半径弦AB于点C,连接AO并延长交于点E,连接EC,若,,则EC的长度为
A.
B.
8
C.
D.
如图,在中,弦的条数是
A.
2
B.
3
C.
4
D.
以上均不正确
如图,点A,B,C在上,,,则
A.
B.
C.
D.
如图,AB是O直径,弦CDAB,垂足为E,若AB,CD,则AE的长为
A.
2
B.
3
C.
4
D.
5
下面四个图形中的角,是圆心角的是
A.
B.
C.
D.
如图,AB是的弦,半径,,则弦AB的长是
A.
B.
C.
D.
如图,AB是的弦,半径于点D,若的半径为5,,则CD的长是
A.
2
B.
3
C.
4
D.
5
如图,四边形ABCD内接于,,,,则的值为
A.
3
B.
C.
D.
不能确定
如图,的直径AB垂直于弦CD于点E,,,则CD的长为
A.
B.
C.
6
D.
12
一个圆的内接正多边形中,一边所对的圆心角为,则该正多边形的边数是
A.
6
B.
5
C.
4
D.
3
二、填空题
已知的半径为5,圆心O到点A的距离为3,则过点A且长度是整数的弦有??????????条
如图,已知AB是的弦,半径OC垂直AB,点D是上一点,且点D与点C位于弦AB两侧,连接AD、CD、OB,若,则______度.
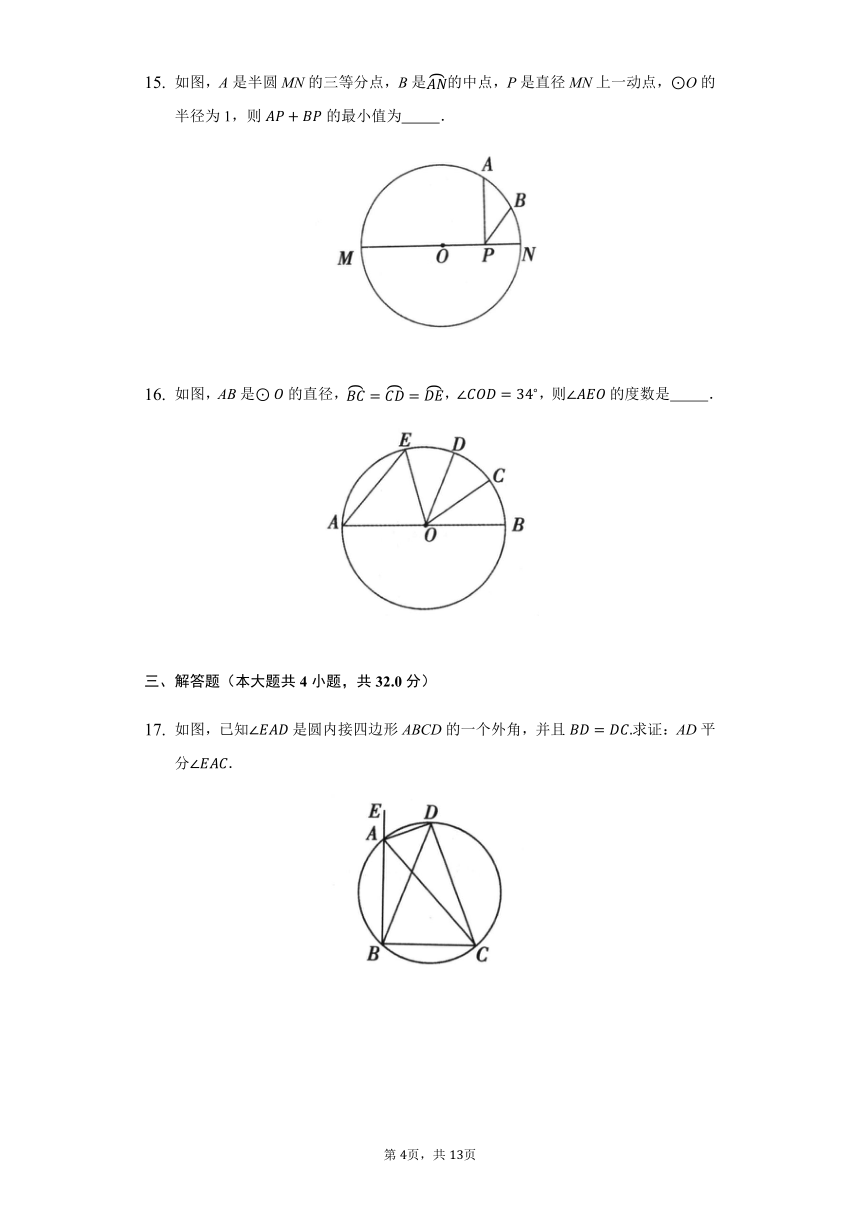
如图,A是半圆MN的三等分点,B是的中点,P是直径MN上一动点,O的半径为1,则的最小值为??????????.
如图,AB是的直径,,,则的度数是??????????.
三、解答题(本大题共4小题,共32.0分)
如图,已知是圆内接四边形ABCD的一个外角,并且求证:AD平分.
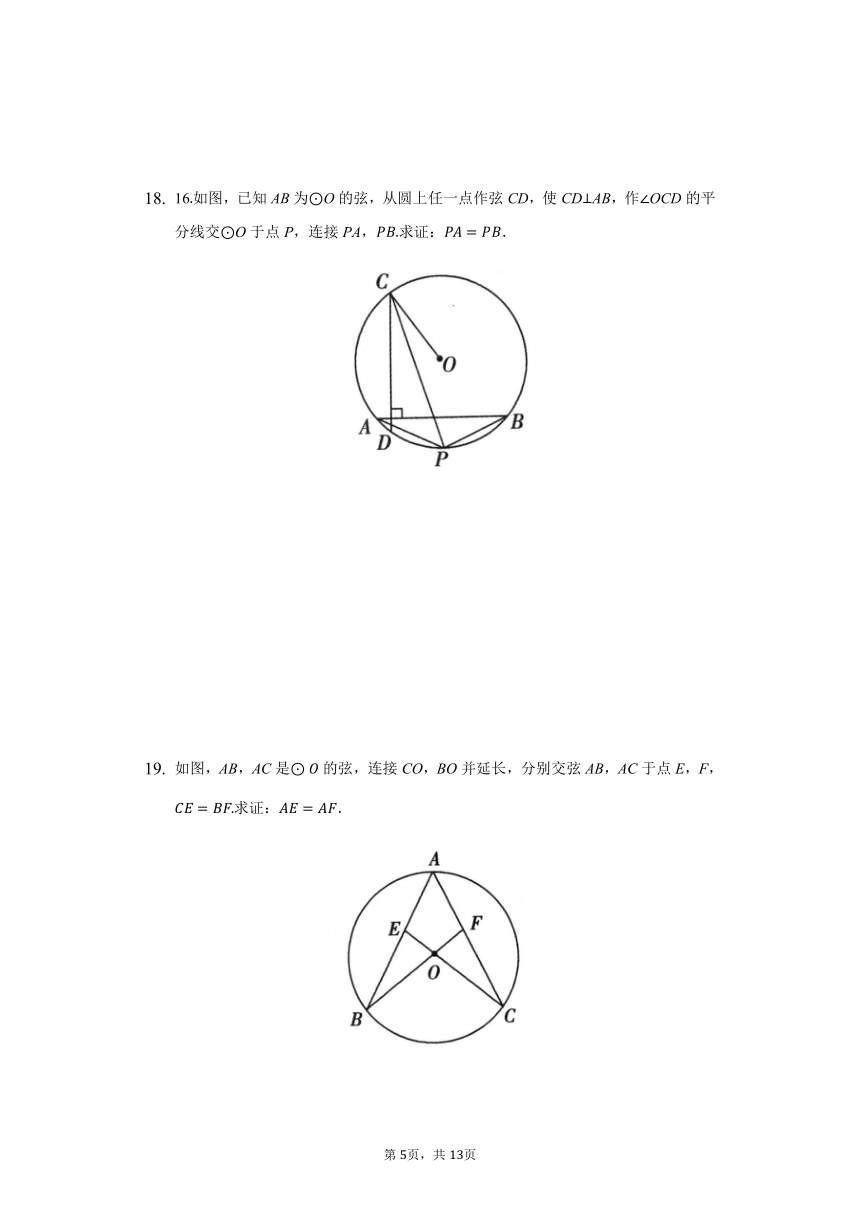
16如图,已知AB为O的弦,从圆上任一点作弦CD,使CDAB,作OCD的平分线交O于点P,连接PA,求证:.
如图,AB,AC是的弦,连接CO,BO并延长,分别交弦AB,AC于点E,F,求证:.
如图,已知AB是的直径,CD是的弦,AB,CD的延长线相交于点E,连接若,,求及的度数.
答案和解析
A
解:一条直线如果具备经过圆心、垂直于弦、平分弦被平分的弦不是直径、平分弦所对的优弧、平分弦所对的劣弧这五条中的任意两条,必然具备其余三条.
若该弦不是直径,满足平分优弧、平分劣弧两个条件,若该弦是直径,易知正确,所以正确
只满足其中的一个条件,所以不正确
要考虑到特殊情况,条件中的弦有可能是直径,所以不正确,
2.D
解:连接AE,
为直径,
,
,
,
.
3.D
解:如图,连接BE,设的半径为R,
,,
在中,,,
由勾股定理,得,
,解得,
,
是AE的中点,C是AB的中点,
是三角形ABE的中位线,
,
为的直径,
,
在中,.
4C
】解:由题图,可得在O中,有弦AB、弦CD、弦BC、弦BD,共4条.
故选C.
5.C
解:连接OA,
,
,
,
,
,
6.A
解:连结OC,如图,直径,
,
,
,
在中,,,
,
.
故选A.
7.D
解:顶点在圆外,故不是圆心角;
B.顶点在圆周上,故不是圆心角;
C.顶点在圆内,但不在圆心,故不是圆心角;
D.是圆心角.
故选D.
8.B
解:过O作于C.
在中,,,,
则,,
因此.
9.A
解:,
,
在中,,,
,
.
10.A
解:如图,过点B作于E,交DC的延长线于F.
,
,
,
,,
≌,
,,
,,,
≌,
,
,
,,
,
,
,
11.B
解:,
,,
,
为等腰直角三角形,
,
.
12.B
解:设正多边形的边数为n.
由题意,
,
13.4
解:如图,EB为过点A的直径,CD为过点A且与EB垂直的弦,
则EB为过点A的最长弦,CD为过点A的最短弦.
连接OC,则,
在中,,,
,.
过点A的最长弦,最短弦,
过点A的弦的长度的取值范围是大于等于8小于等于10,又长度是整数,
过点A的弦的长度为8,9,10,由圆的轴对称性,知长度为9的弦有2条,
过点A且长度是整数的弦有4条.
14.35
解:如图,连接OA.
,
,
,
,
15.
解:?如图,作A关于MN的对称点,
根据圆的对称性,得必在圆上,
连接交MN于点P,则此时的值最小,此时,
连接,OB,OA,,
,.
,.,
,即的最小值是.
16.
解:?,
,
.
,
A,
.
17.证明:?四边形ABCD是圆内接四边形,
,
又,
.
,
,
又,
,
即AD平分.
18.证明:如图,连接OP.
,
平分,,
,,
,,
,.
19.证明:?,,.
又,,C.
又,,,.
20.解:连接OD,
,,
,,,
E.
,,.
第2页,共2页
第1页,共1页
一、选择题
下列命题正确的有平分弦所对的两条弧的直线必垂直于弦
垂直于弦的直线平分弦
平分弦的直线必平分弦所对的两条弧
与直径不垂直的弦不能被该直径平分
平分弦的直径必平分弦所对的两条弧.
A.
1个
B.
2个
C.
3个
D.
4个
如图,已知A,B,C,D,E均在上,且AC为直径,则
A.
B.
C.
D.
如图,在中,半径弦AB于点C,连接AO并延长交于点E,连接EC,若,,则EC的长度为
A.
B.
8
C.
D.
如图,在中,弦的条数是
A.
2
B.
3
C.
4
D.
以上均不正确
如图,点A,B,C在上,,,则
A.
B.
C.
D.
如图,AB是O直径,弦CDAB,垂足为E,若AB,CD,则AE的长为
A.
2
B.
3
C.
4
D.
5
下面四个图形中的角,是圆心角的是
A.
B.
C.
D.
如图,AB是的弦,半径,,则弦AB的长是
A.
B.
C.
D.
如图,AB是的弦,半径于点D,若的半径为5,,则CD的长是
A.
2
B.
3
C.
4
D.
5
如图,四边形ABCD内接于,,,,则的值为
A.
3
B.
C.
D.
不能确定
如图,的直径AB垂直于弦CD于点E,,,则CD的长为
A.
B.
C.
6
D.
12
一个圆的内接正多边形中,一边所对的圆心角为,则该正多边形的边数是
A.
6
B.
5
C.
4
D.
3
二、填空题
已知的半径为5,圆心O到点A的距离为3,则过点A且长度是整数的弦有??????????条
如图,已知AB是的弦,半径OC垂直AB,点D是上一点,且点D与点C位于弦AB两侧,连接AD、CD、OB,若,则______度.
如图,A是半圆MN的三等分点,B是的中点,P是直径MN上一动点,O的半径为1,则的最小值为??????????.
如图,AB是的直径,,,则的度数是??????????.
三、解答题(本大题共4小题,共32.0分)
如图,已知是圆内接四边形ABCD的一个外角,并且求证:AD平分.
16如图,已知AB为O的弦,从圆上任一点作弦CD,使CDAB,作OCD的平分线交O于点P,连接PA,求证:.
如图,AB,AC是的弦,连接CO,BO并延长,分别交弦AB,AC于点E,F,求证:.
如图,已知AB是的直径,CD是的弦,AB,CD的延长线相交于点E,连接若,,求及的度数.
答案和解析
A
解:一条直线如果具备经过圆心、垂直于弦、平分弦被平分的弦不是直径、平分弦所对的优弧、平分弦所对的劣弧这五条中的任意两条,必然具备其余三条.
若该弦不是直径,满足平分优弧、平分劣弧两个条件,若该弦是直径,易知正确,所以正确
只满足其中的一个条件,所以不正确
要考虑到特殊情况,条件中的弦有可能是直径,所以不正确,
2.D
解:连接AE,
为直径,
,
,
,
.
3.D
解:如图,连接BE,设的半径为R,
,,
在中,,,
由勾股定理,得,
,解得,
,
是AE的中点,C是AB的中点,
是三角形ABE的中位线,
,
为的直径,
,
在中,.
4C
】解:由题图,可得在O中,有弦AB、弦CD、弦BC、弦BD,共4条.
故选C.
5.C
解:连接OA,
,
,
,
,
,
6.A
解:连结OC,如图,直径,
,
,
,
在中,,,
,
.
故选A.
7.D
解:顶点在圆外,故不是圆心角;
B.顶点在圆周上,故不是圆心角;
C.顶点在圆内,但不在圆心,故不是圆心角;
D.是圆心角.
故选D.
8.B
解:过O作于C.
在中,,,,
则,,
因此.
9.A
解:,
,
在中,,,
,
.
10.A
解:如图,过点B作于E,交DC的延长线于F.
,
,
,
,,
≌,
,,
,,,
≌,
,
,
,,
,
,
,
11.B
解:,
,,
,
为等腰直角三角形,
,
.
12.B
解:设正多边形的边数为n.
由题意,
,
13.4
解:如图,EB为过点A的直径,CD为过点A且与EB垂直的弦,
则EB为过点A的最长弦,CD为过点A的最短弦.
连接OC,则,
在中,,,
,.
过点A的最长弦,最短弦,
过点A的弦的长度的取值范围是大于等于8小于等于10,又长度是整数,
过点A的弦的长度为8,9,10,由圆的轴对称性,知长度为9的弦有2条,
过点A且长度是整数的弦有4条.
14.35
解:如图,连接OA.
,
,
,
,
15.
解:?如图,作A关于MN的对称点,
根据圆的对称性,得必在圆上,
连接交MN于点P,则此时的值最小,此时,
连接,OB,OA,,
,.
,.,
,即的最小值是.
16.
解:?,
,
.
,
A,
.
17.证明:?四边形ABCD是圆内接四边形,
,
又,
.
,
,
又,
,
即AD平分.
18.证明:如图,连接OP.
,
平分,,
,,
,,
,.
19.证明:?,,.
又,,C.
又,,,.
20.解:连接OD,
,,
,,,
E.
,,.
第2页,共2页
第1页,共1页
同课章节目录
