人教版八年级上册12.1全等三角形课件(20张)
文档属性
| 名称 | 人教版八年级上册12.1全等三角形课件(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 529.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-04 13:48:28 | ||
图片预览



文档简介
(共20张PPT)
12.1
全等三角形
学习目标
1.了解全等形和全等三角形的概念,掌握全等三角形的性质。
2.能够找出全等三角形的对应顶点、对应边、对应角。
自
学
指
导
认真看
P31-32,思考以下问题:
1.什么叫全等形?什么叫全等三角形?
2.什么叫对应顶点?对应边?对应角?
3.哪些图形变换是全等三角形?
4.看
P32小贴士,记两个三角形全等时注意什么?
5.全等三角形有哪些性质?
6.先完成的同学参照32页第1题,思考怎样找全等三角形的对应边与对应角?
如有疑问,可小声问同学或举手问老师.
5分钟后,比谁能熟背以上概念与性质。
(1)
(2)
(3)
提问1
能够完全重合的两个图形叫做全等形
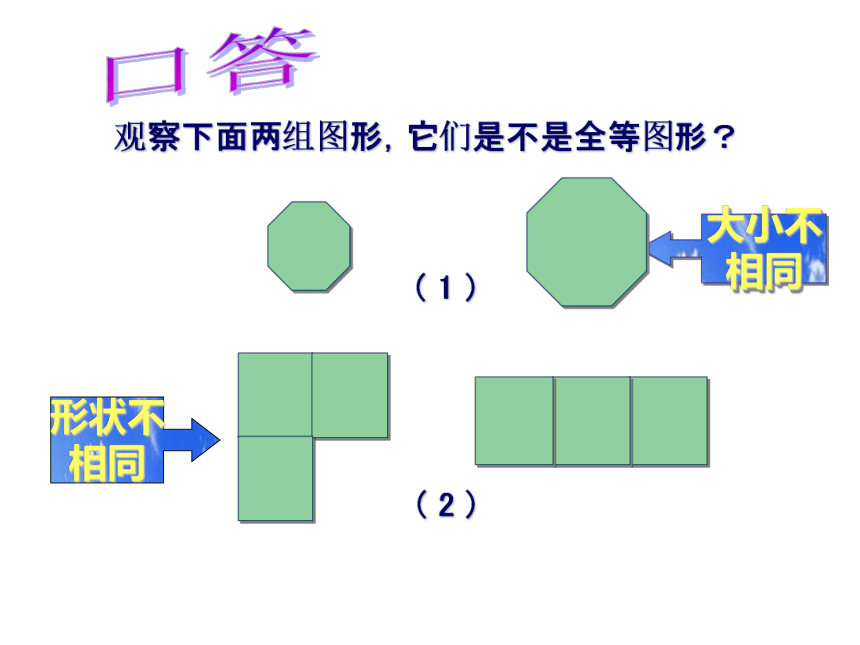
大小不
相同
形状不
相同
观察下面两组图形,它们是不是全等图形?
(
1
)
(
2
)
口答
A
B
C
E
D
F
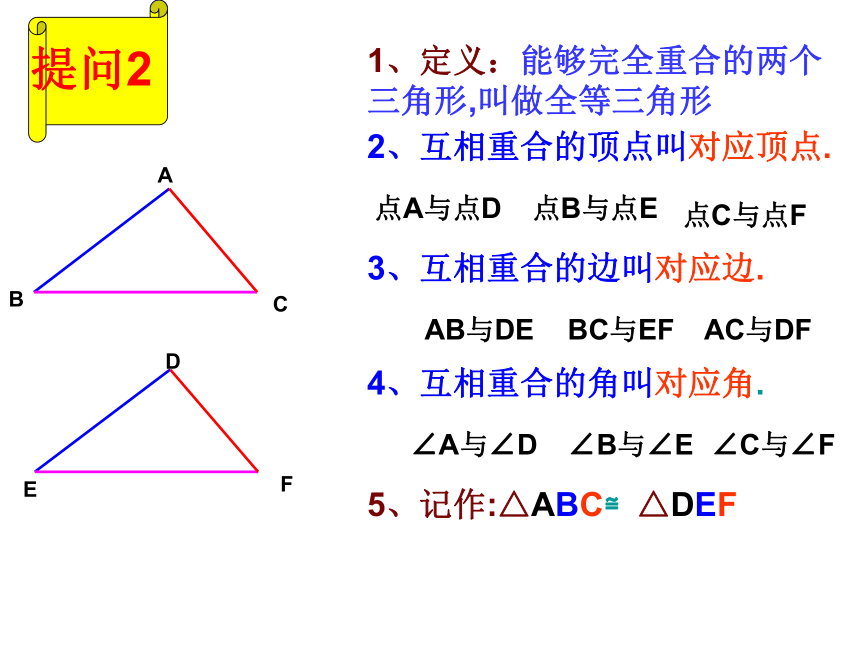
1、定义:能够完全重合的两个三角形,叫做全等三角形
5、记作:△ABC≌△DEF
2、互相重合的顶点叫对应顶点.
3、互相重合的边叫对应边.
4、互相重合的角叫对应角.
点A与点D
点B与点E
点C与点F
AB与DE
BC与EF
AC与DF
∠A与∠D
∠B与∠E
∠C与∠F
提问2
N
M
S
O
T
D
C
O
A
B
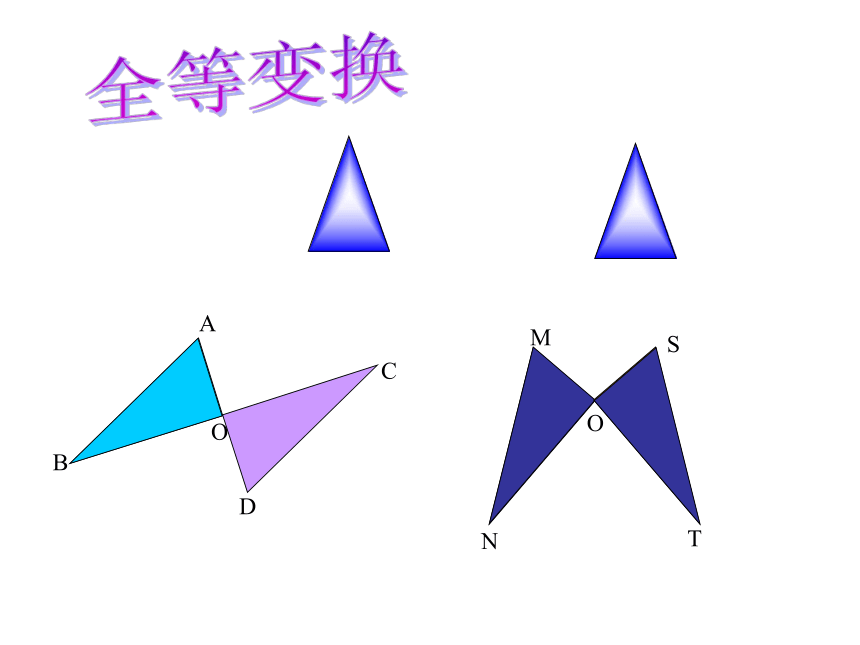
全等变换
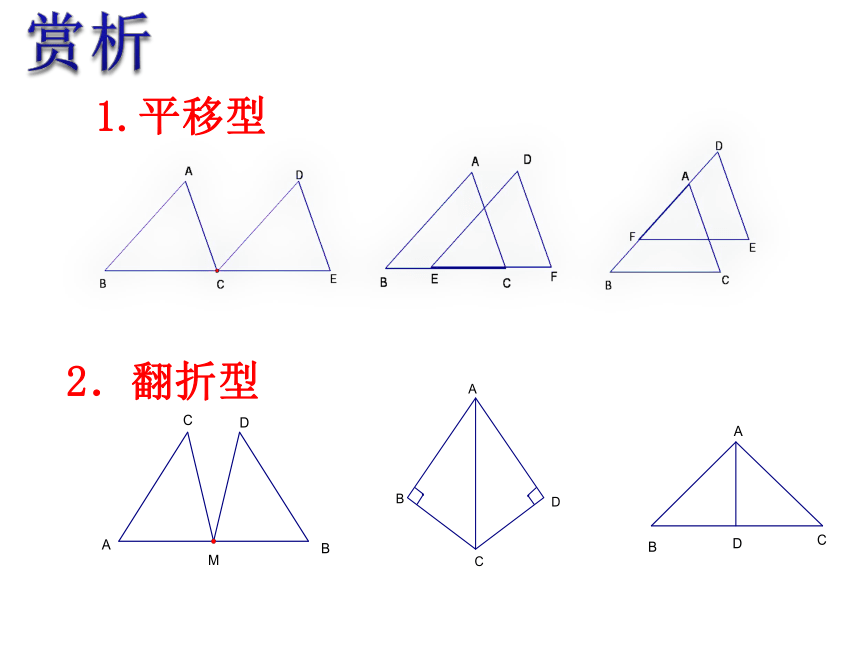
2.翻折型
1.平移型
赏析
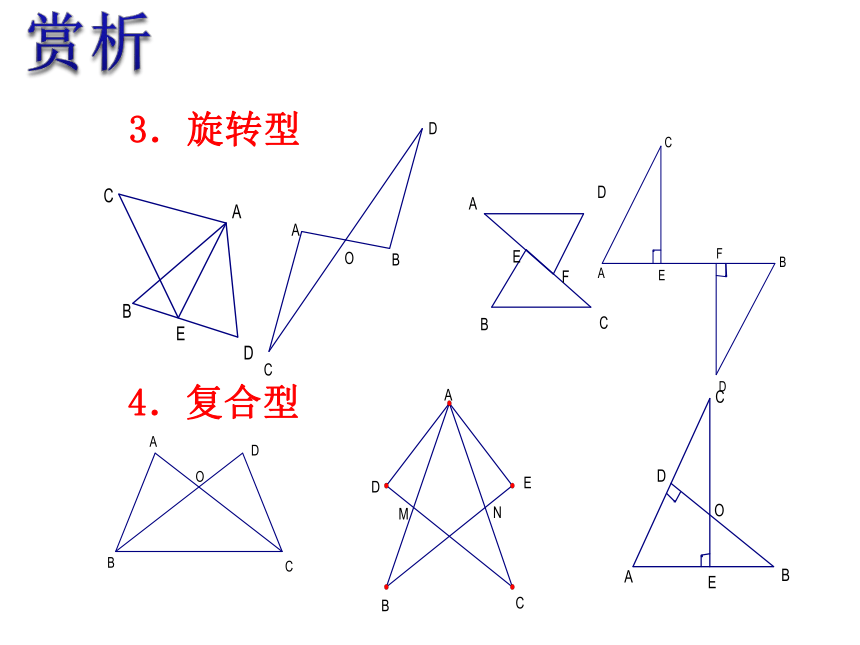
3.旋转型
4.复合型
赏析
全等三角形性质
A
B
C
E
D
F
∵△ABC≌△DEF(已知)
∴AB=DE,
AC=DF,BC=EF
∠A=∠D,
∠B=∠E,
∠C=∠F
文字叙述:全等三角形对应边相等,
全等三角形对应角相等
几何语言
A
B
C
D
E
已知:如图△ABC≌△ADE。
求证
证明
∵
△ABC≌
△ADE(已知)
∴
∠DAE=
;(
)
∴
∠DAE
-
∠BAE=∠BAC
–(
)
∠DAB=
。
∠BAC
∠CAE
∠DAB=
全等三角形对应角相等
∠BAE
∠CAE
口答
1、若△AOC≌△BOD,AC=
∠A=
A
B
O
C
D
2、若△ABD≌△ACE,BD= ,
∠BDA=
3、若△ABC≌△CDA,AB=
∠BAC=
A
B
C
D
请填空
BD
∠B
CE
∠CEA
CD
∠DCA
A
B
C
D
E
公共点
公共角
公共边
口答
1、有公共边
A
B
C
D
A
B
C
D
A
B
C
D
2、有公共顶点
A
B
C
D
O
A
B
C
D
O
A
B
C
D
E
A
B
D
C
E
自学检测
要求:
1、认真审题,书写规范
2、3分钟后比一比谁能全做对,加油!
如图,△OAC≌△OBD,点C和点B,点A和点D
是对应点。说出这两个三角形中相等的边和角。
C
A
D
B
O
自学检测答案
1、解:相等的边有:
AC=DB,
AO=DO,
CO=BO
相等的角有:
∠A=
∠D
∠C=
∠B
∠AOC=
∠DOB
自学检测
如图,△ABN≌△ACM,∠C和∠B是对应角,
AB和AC是对应边。写出其他对应边及对应角。
要求:
1、认真审题,书写规范
2、3分钟后比一比谁能全做对,加油!
A
B
C
M
N
2、对应边有
AM与AN
BN与CM
对应角有
∠BAN与
∠CAM
∠ANB与∠AMC
课堂小结
1、回忆这节课,学习了全等三角形的哪些知识?
全等三角形的概念、性质、表示方法、对应写法等
2、找全等三角形对应边、对应角的方法
1、大边对应大边,大角对应大角
2、公共边是对应边,公共角是对应角
3、对应边所对的角是对应角,对应角 所对的边是对应边
4、根据书写规范,按照对应顶点找对应边或对应角;
当堂训练
1.下列图形是全等图形的是( )
2.下列说法:①全等三角形的面积相等;②全等三角形的周长相等;③全等三角形的对应角相等;④全等三角形的对应边相等.其中正确的有( )(A)1个
(B)2个
(C)3个
(D)4个
D
D
(A)20°
(B)30°(C)35°
(D)40°
3.如图,△ACB≌△A′CB′,∠ACA′=30°,则∠BCB′的度数为( )
B
4.如图,已知△ABC≌△DCB,AB=10,∠A=60°,
∠ABC=80°,那么下列结论中错误的是(
)
(A)∠D=60°
(B)∠DBC=40°
(C)AC=DB
(D)BE=10
D
5、如图,△ABC≌△BAD,若AB=9,AC=5,BC=7,则△BAD的周长为
.
6、如图,将△ABC沿DE折叠,使点C落在AB边上的点P处.若∠CDE=50°,∠DEC=68°,则∠DPE=
度.
62
21
8、如图,△ABC≌△DEF,AB和DE是对应边,∠A和∠D是对应角,找出图中所有相等的线段和角.
7、如图,△ADB≌△EDB≌△EDC,B,E,C在一条直线上,则∠C的度数
为
.
30°
解:相等的线段有:
AB=DE,
AC=DF,
BC=EF,
AF=DC
相等的角有:
∠A=
∠D
∠E=
∠B
∠ACB=
∠DFE
∠DCB=
∠EFA
12.1
全等三角形
学习目标
1.了解全等形和全等三角形的概念,掌握全等三角形的性质。
2.能够找出全等三角形的对应顶点、对应边、对应角。
自
学
指
导
认真看
P31-32,思考以下问题:
1.什么叫全等形?什么叫全等三角形?
2.什么叫对应顶点?对应边?对应角?
3.哪些图形变换是全等三角形?
4.看
P32小贴士,记两个三角形全等时注意什么?
5.全等三角形有哪些性质?
6.先完成的同学参照32页第1题,思考怎样找全等三角形的对应边与对应角?
如有疑问,可小声问同学或举手问老师.
5分钟后,比谁能熟背以上概念与性质。
(1)
(2)
(3)
提问1
能够完全重合的两个图形叫做全等形
大小不
相同
形状不
相同
观察下面两组图形,它们是不是全等图形?
(
1
)
(
2
)
口答
A
B
C
E
D
F
1、定义:能够完全重合的两个三角形,叫做全等三角形
5、记作:△ABC≌△DEF
2、互相重合的顶点叫对应顶点.
3、互相重合的边叫对应边.
4、互相重合的角叫对应角.
点A与点D
点B与点E
点C与点F
AB与DE
BC与EF
AC与DF
∠A与∠D
∠B与∠E
∠C与∠F
提问2
N
M
S
O
T
D
C
O
A
B
全等变换
2.翻折型
1.平移型
赏析
3.旋转型
4.复合型
赏析
全等三角形性质
A
B
C
E
D
F
∵△ABC≌△DEF(已知)
∴AB=DE,
AC=DF,BC=EF
∠A=∠D,
∠B=∠E,
∠C=∠F
文字叙述:全等三角形对应边相等,
全等三角形对应角相等
几何语言
A
B
C
D
E
已知:如图△ABC≌△ADE。
求证
证明
∵
△ABC≌
△ADE(已知)
∴
∠DAE=
;(
)
∴
∠DAE
-
∠BAE=∠BAC
–(
)
∠DAB=
。
∠BAC
∠CAE
∠DAB=
全等三角形对应角相等
∠BAE
∠CAE
口答
1、若△AOC≌△BOD,AC=
∠A=
A
B
O
C
D
2、若△ABD≌△ACE,BD= ,
∠BDA=
3、若△ABC≌△CDA,AB=
∠BAC=
A
B
C
D
请填空
BD
∠B
CE
∠CEA
CD
∠DCA
A
B
C
D
E
公共点
公共角
公共边
口答
1、有公共边
A
B
C
D
A
B
C
D
A
B
C
D
2、有公共顶点
A
B
C
D
O
A
B
C
D
O
A
B
C
D
E
A
B
D
C
E
自学检测
要求:
1、认真审题,书写规范
2、3分钟后比一比谁能全做对,加油!
如图,△OAC≌△OBD,点C和点B,点A和点D
是对应点。说出这两个三角形中相等的边和角。
C
A
D
B
O
自学检测答案
1、解:相等的边有:
AC=DB,
AO=DO,
CO=BO
相等的角有:
∠A=
∠D
∠C=
∠B
∠AOC=
∠DOB
自学检测
如图,△ABN≌△ACM,∠C和∠B是对应角,
AB和AC是对应边。写出其他对应边及对应角。
要求:
1、认真审题,书写规范
2、3分钟后比一比谁能全做对,加油!
A
B
C
M
N
2、对应边有
AM与AN
BN与CM
对应角有
∠BAN与
∠CAM
∠ANB与∠AMC
课堂小结
1、回忆这节课,学习了全等三角形的哪些知识?
全等三角形的概念、性质、表示方法、对应写法等
2、找全等三角形对应边、对应角的方法
1、大边对应大边,大角对应大角
2、公共边是对应边,公共角是对应角
3、对应边所对的角是对应角,对应角 所对的边是对应边
4、根据书写规范,按照对应顶点找对应边或对应角;
当堂训练
1.下列图形是全等图形的是( )
2.下列说法:①全等三角形的面积相等;②全等三角形的周长相等;③全等三角形的对应角相等;④全等三角形的对应边相等.其中正确的有( )(A)1个
(B)2个
(C)3个
(D)4个
D
D
(A)20°
(B)30°(C)35°
(D)40°
3.如图,△ACB≌△A′CB′,∠ACA′=30°,则∠BCB′的度数为( )
B
4.如图,已知△ABC≌△DCB,AB=10,∠A=60°,
∠ABC=80°,那么下列结论中错误的是(
)
(A)∠D=60°
(B)∠DBC=40°
(C)AC=DB
(D)BE=10
D
5、如图,△ABC≌△BAD,若AB=9,AC=5,BC=7,则△BAD的周长为
.
6、如图,将△ABC沿DE折叠,使点C落在AB边上的点P处.若∠CDE=50°,∠DEC=68°,则∠DPE=
度.
62
21
8、如图,△ABC≌△DEF,AB和DE是对应边,∠A和∠D是对应角,找出图中所有相等的线段和角.
7、如图,△ADB≌△EDB≌△EDC,B,E,C在一条直线上,则∠C的度数
为
.
30°
解:相等的线段有:
AB=DE,
AC=DF,
BC=EF,
AF=DC
相等的角有:
∠A=
∠D
∠E=
∠B
∠ACB=
∠DFE
∠DCB=
∠EFA
