华师版数学九年级下册 第26章达标测试卷 (word版,含答案)
文档属性
| 名称 | 华师版数学九年级下册 第26章达标测试卷 (word版,含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 182.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-30 22:46:16 | ||
图片预览



文档简介
第26章达标测试卷
一、选择题(每题3分,共30分)
1.下列函数关系式中,是二次函数的是( )
A.y=x3-2x2-1 B.y=x2 C.y=-3 D.y=x+1
2.抛物线y=x2-4的顶点坐标是( )
A.(0,-4) B.(0,4) C.(2,0) D.(-2,0)
3.已知二次函数y=x2+2x+4,若y随x的增大而减小,则x的取值范围是( )
A.x>-1 B.x<-1 C.x>1 D.x<1
4.如图是有相同对称轴的两条抛物线,下列关系不正确的是( )
A.h=m B.k=n C.k>n D.h<0,k>0
(第4题) (第5题)
5.如图是一副眼镜镜片下半部分轮廓对应的两条抛物线(它们关于y轴对称).AB∥x轴,AB=4 cm,最低点C在x轴上,高CH=1 cm,BD=2 cm,则右轮廓线DFE所在抛物线对应的函数表达式为( )
A.y=(x+3)2 B.y=-(x+3)2
C.y=(x-3)2 D.y=-(x-3)2
6.在直角坐标系中,将二次函数y=-2(x-1)2-2的图象向左平移1个单位,再向上平移1个单位,则平移后图象顶点为( )
A.(0,0) B.(1,-2) C.(0,-1) D.(-2,1)
7.函数y=与y=-kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
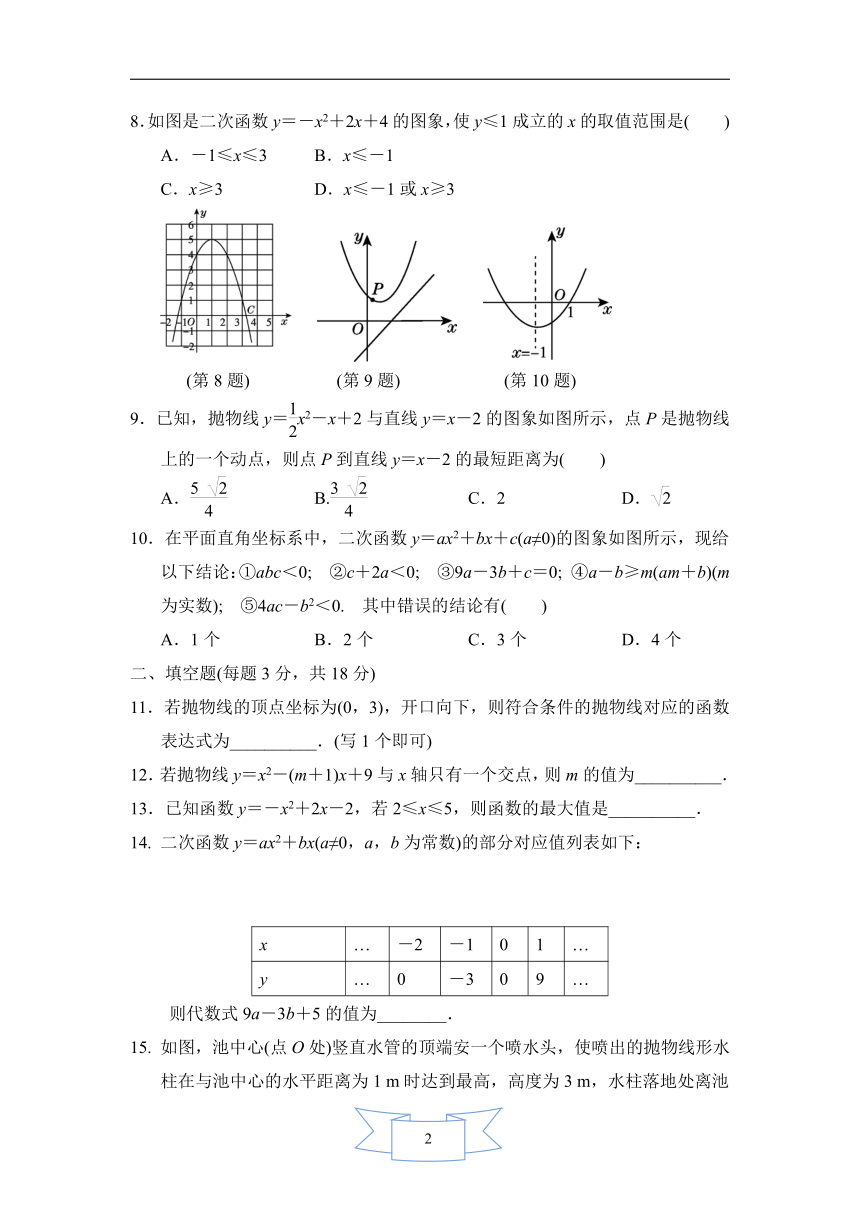
8.如图是二次函数y=-x2+2x+4的图象,使y≤1成立的x的取值范围是( )
A.-1≤x≤3 B.x≤-1
C.x≥3 D.x≤-1或x≥3
(第8题) (第9题) (第10题)
9.已知,抛物线y=x2-x+2与直线y=x-2的图象如图所示,点P是抛物线上的一个动点,则点P到直线y=x-2的最短距离为( )
A. B. C.2 D.
10.在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示,现给以下结论:①abc<0; ②c+2a<0; ③9a-3b+c=0; ④a-b≥m(am+b)(m为实数); ⑤4ac-b2<0. 其中错误的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每题3分,共18分)
11.若抛物线的顶点坐标为(0,3),开口向下,则符合条件的抛物线对应的函数表达式为__________.(写1个即可)
12.若抛物线y=x2-(m+1)x+9与x轴只有一个交点,则m的值为__________.
13.已知函数y=-x2+2x-2,若2≤x≤5,则函数的最大值是__________.
14. 二次函数y=ax2+bx(a≠0,a,b为常数)的部分对应值列表如下:
x … -2 -1 0 1 …
y … 0 -3 0 9 …
则代数式9a-3b+5的值为________.
15. 如图,池中心(点O处)竖直水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1 m时达到最高,高度为3 m,水柱落地处离池中心3 m,则水管的长为__________.
(第15题)
16.已知a,b为抛物线y=(x-c)(x-c-d)-2与x轴交点的横坐标,a<b,则|a-c|+|c-b|的值为________.
三、解答题(17~20题每题8分,21~22题每题10分,共52分)
17.用配方法把函数y=-3x2-6x+10化成y=a(x-h)2+k的形式,然后指出它的图象的开口方向,对称轴和顶点坐标.
18.二次函数的图象经过点A(1,3),B(2,4),且点B是该二次函数图象的顶点.求二次函数表达式,并画出图象.
19.如图,二次函数y1=ax2+c的图象与反比例函数y2=的图象相交于A,B两点,根据图中信息解答下列问题.
(第19题)
(1)求反比例函数和二次函数的表达式;
(2)当y1>y2时,求x的取值范围.
20.某服装超市购进单价为30元的童装若干件,物价部门规定其销售单价不低于30元,不高于60元.销售一段时间后发现:当销售单价为60元时,平均每月销售量为80件,而当销售单价每降低1元时,平均每月能多售出2件.同时,在销售过程中,每月还要支付其他费用450元.设销售单价为x元,平均月销售量为y件.
(1)求出y与x的函数关系式,并写出自变量x的取值范围.
(2)当销售单价为多少元时,销售这种童装平均每月可获利1 800元?
(3)当销售单价为多少元时,销售这种童装平均每月获得利润最大?最大利润是多少?
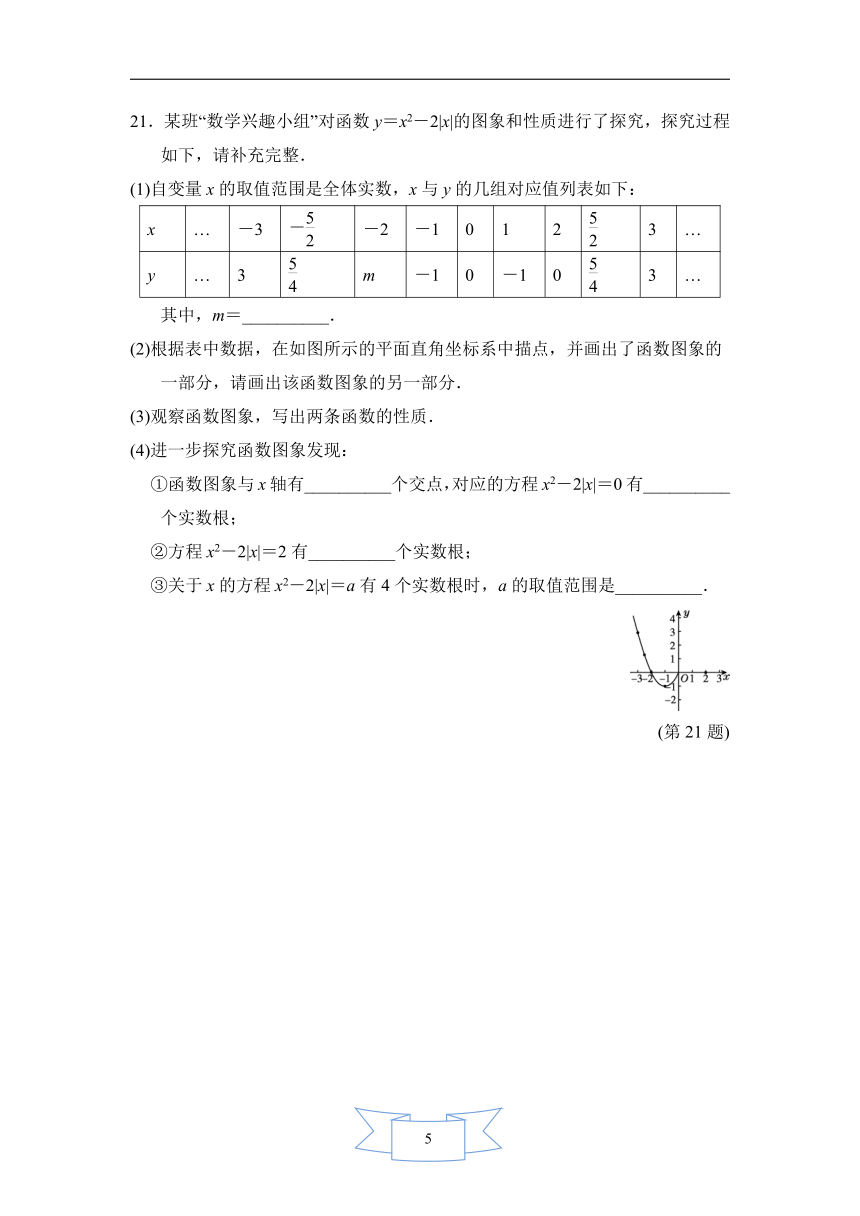
21.某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x … -3 - -2 -1 0 1 2
3 …
y … 3
m -1 0 -1 0
3 …
其中,m=__________.
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出两条函数的性质.
(4)进一步探究函数图象发现:
①函数图象与x轴有__________个交点,对应的方程x2-2|x|=0有__________
个实数根;
②方程x2-2|x|=2有__________个实数根;
③关于x的方程x2-2|x|=a有4个实数根时,a的取值范围是__________.
(第21题)
22.抛物线y=ax2+bx+c经过A(-1,0),B(4,0),C(0,3)三点,D为直线BC上方抛物线上一动点,DE⊥BC于E.
(第22题)
(1)求抛物线对应的函数表达式;
(2)如图①,求线段DE长度的最大值;
(3)如图②,设AB的中点为F,连结CD,CF.是否存在点D,使得△CDE中有一个角与∠CFO相等?若存在,求点D的横坐标;若不存在,请说明理由.
答案
一、1. B 2. A 3. B 4. B 5. C
6. C 7. B 8. D
9.D 点拨:设过点P且平行于直线y=x-2的直线的表达式为y=x+b,当直线y=x+b与抛物线只有一个交点P时,点P到直线y=x-2的距离最小,由
消去y得x2-4x+4-2b=0,
当Δ=0时,16-16+8b=0,
解得b=0,
∴直线的表达式为y=x.
如图,作OC⊥AB于点C,
设直线y=x-2交x轴于A,交y轴于B,则A(2,0),B(0,-2),
∴OA=OB=2,
∴AB=2 .
∵OC⊥AB,
∴OC=AB=.故选D.
(第9题)
10.A 点拨:①由抛物线可知:a>0,c<0,-<0,
∴b>0,
∴abc<0,故①正确;
②由对称轴可知:-=-1,
∴b=2a,
又∵x=1时,y=a+b+c=0,
∴c+3a=0,
∴c+2a=-3a+2a=-a<0,故②正确;
③点(1,0)关于直线x=-1的对称点为(-3,0),
∴x=-3时,y=9a-3b+c=0,故③正确;
④当x=-1时,y取最小值a-b+c,∴am2+bm+c≥a-b+c,
即a-b≤m(am+b),故④错误;
⑤抛物线与x轴有两个交点,
∴Δ>0,即b2-4ac>0,
∴4ac-b2<0,故⑤正确.故选A.
二、11.(答案不唯一)y=-x2+3
12. -7或5 13.-2
14.14 点拨:∵x=0和x=-2时y的值相同,都是0,
∴点和点关于二次函数图象的对称轴对称,
∴对称轴为直线x==-1.
∵横坐标为-3和1的点关于二次函数图象的对称轴对称,
∴x=-3时对应的函数值y=9,
∴9a-3b=9,
∴9a-3b+5=14.
15.2.25 m 点拨:因为水柱在与池中心的水平距离为1 m时达到最高,高度为3 m,
所以可设抛物线对应的函数表达式为y=a(x-1)2+3(0≤x≤3),把(3,0)代入得a=-,
所以y=-(x-1)2+3(0≤x≤3).
令x=0,则y==2.25,
即水管的长为2.25 m.
16. b-a 点拨:当x=c时,y=-2<0,
又∵当x=a和x=b时,y=0,抛物线开口向上,
∴a<c<b,则|a-c|+|c-b|=c-a+b-c=b-a.
三、17. 解:y=-3x2-6x+10=-3(x2+2x)+10=-3(x2+2x+1-1)+10=-3(x+1)2+13=-3[x-(-1)]2+13,
它的图象开口向下,对称轴为直线x=-1,顶点坐标为(-1,13).
18. 解:设二次函数的表达式为y=a(x-2)2+4,把(1,3)代入,得3=a+4,解得a=-1,
∴y=-(x-2)2+4=-x2+4x,
∴二次函数表达式为y=-x2+4x.
画出图象略.
19. 解:(1)把A(-2,1)的坐标代入y2=,得m=-2,
所以反比例函数的表达式为y2=-.
把B(1,n)的坐标代入y2=-,
得n=-2,所以B点坐标为(1,-2).把A(-2,1),B(1,-2)的坐标代入y1=ax2+c,得
解得
所以二次函数的表达式为y1=x2-3.
(2)观察图象可得,当y1>y2时,x<-2或x>0且x≠1.
20. 解:(1)由题意得y=80+2(60-x),
∴函数的关系式为y=-2x+200 (30≤x≤60).
(2)由题意得(x-30)(-2x+200)-450=1 800,解得x1=55,x2=75(不符合题意,舍去).
答:当销售单价为55元时,销售这种童装平均每月可获利1 800元.
(3)设每月获得的利润为w元,由题意得w=(x-30)(-2x+200)-450=-2(x-65)2+2 000.
∵-2<0,
∴当x≤65时,w随x的增大而增大.
又∵30≤x≤60,
∴当x=60时,w取最大值,w最大=-2×(60-65)2+2 000=1 950.
答:当销售单价为60元时,销售这种童装平均每月获得利润最大,最大利润是1 950元.
21. 解:(1)0 (2)如图.
(3)①函数y=x2-2|x|的图象关于y轴对称;②当x>1时,y随x的增大而增大.
(4)①3;3 ②2 ③-1(第21题)
点拨:(3)题答案不唯一.
22. 解:(1)由题意得,解得
∴抛物线对应的函数表达式为y=-x2+x+3.
(2)设直线BC对应的函数表达式为y=kx+d,则解得
∴y=-x+3.
设D(m,-m2+m+3)(0<m<4).过点D作DM⊥x轴交BC于点M,则M,DM∥OC,
∴DM=-=-m2+3m,
∠DME=∠OCB,
又∵∠DEM=∠BOC=90°,
∴△DEM∽△BOC,
∴=.
∵OB=4,OC=3,
∴BC=5,
∴DE=DM,
∴DE=-m2+m=-(m-2)2+(0当m=2时,DE取最大值,最大值是.
(3)存在.
∵点F为AB的中点,
∴OF=,
∴tan∠CFO==2.
如图,过点B作BG⊥BC,交CD的延长线于G点,过点G作GH⊥x轴,垂足为H.
(第22题)
①若∠DCE=∠CFO,
则tan∠DCE==2,
∴BG=10.
易得△GBH∽△BCO,
∴==,
∴GH=8,BH=6,
∴G(10,8).
设直线CG对应的函数表达式为y=px+n,
∴解得
∴直线CG对应的函数表达式为y=x+3,
令x+3=-x2+x+3,
解得x=或x=0(舍去).
②若∠CDE=∠CFO,
同理可得BG=,GH=2,BH=,
∴G.
易得直线CG对应的函数表达式为y=-x+3,
令-x+3=-x2+x+3,
解得x=或x=0(舍去).
综上所述,点D的横坐标为或.
一、选择题(每题3分,共30分)
1.下列函数关系式中,是二次函数的是( )
A.y=x3-2x2-1 B.y=x2 C.y=-3 D.y=x+1
2.抛物线y=x2-4的顶点坐标是( )
A.(0,-4) B.(0,4) C.(2,0) D.(-2,0)
3.已知二次函数y=x2+2x+4,若y随x的增大而减小,则x的取值范围是( )
A.x>-1 B.x<-1 C.x>1 D.x<1
4.如图是有相同对称轴的两条抛物线,下列关系不正确的是( )
A.h=m B.k=n C.k>n D.h<0,k>0
(第4题) (第5题)
5.如图是一副眼镜镜片下半部分轮廓对应的两条抛物线(它们关于y轴对称).AB∥x轴,AB=4 cm,最低点C在x轴上,高CH=1 cm,BD=2 cm,则右轮廓线DFE所在抛物线对应的函数表达式为( )
A.y=(x+3)2 B.y=-(x+3)2
C.y=(x-3)2 D.y=-(x-3)2
6.在直角坐标系中,将二次函数y=-2(x-1)2-2的图象向左平移1个单位,再向上平移1个单位,则平移后图象顶点为( )
A.(0,0) B.(1,-2) C.(0,-1) D.(-2,1)
7.函数y=与y=-kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
8.如图是二次函数y=-x2+2x+4的图象,使y≤1成立的x的取值范围是( )
A.-1≤x≤3 B.x≤-1
C.x≥3 D.x≤-1或x≥3
(第8题) (第9题) (第10题)
9.已知,抛物线y=x2-x+2与直线y=x-2的图象如图所示,点P是抛物线上的一个动点,则点P到直线y=x-2的最短距离为( )
A. B. C.2 D.
10.在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示,现给以下结论:①abc<0; ②c+2a<0; ③9a-3b+c=0; ④a-b≥m(am+b)(m为实数); ⑤4ac-b2<0. 其中错误的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每题3分,共18分)
11.若抛物线的顶点坐标为(0,3),开口向下,则符合条件的抛物线对应的函数表达式为__________.(写1个即可)
12.若抛物线y=x2-(m+1)x+9与x轴只有一个交点,则m的值为__________.
13.已知函数y=-x2+2x-2,若2≤x≤5,则函数的最大值是__________.
14. 二次函数y=ax2+bx(a≠0,a,b为常数)的部分对应值列表如下:
x … -2 -1 0 1 …
y … 0 -3 0 9 …
则代数式9a-3b+5的值为________.
15. 如图,池中心(点O处)竖直水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1 m时达到最高,高度为3 m,水柱落地处离池中心3 m,则水管的长为__________.
(第15题)
16.已知a,b为抛物线y=(x-c)(x-c-d)-2与x轴交点的横坐标,a<b,则|a-c|+|c-b|的值为________.
三、解答题(17~20题每题8分,21~22题每题10分,共52分)
17.用配方法把函数y=-3x2-6x+10化成y=a(x-h)2+k的形式,然后指出它的图象的开口方向,对称轴和顶点坐标.
18.二次函数的图象经过点A(1,3),B(2,4),且点B是该二次函数图象的顶点.求二次函数表达式,并画出图象.
19.如图,二次函数y1=ax2+c的图象与反比例函数y2=的图象相交于A,B两点,根据图中信息解答下列问题.
(第19题)
(1)求反比例函数和二次函数的表达式;
(2)当y1>y2时,求x的取值范围.
20.某服装超市购进单价为30元的童装若干件,物价部门规定其销售单价不低于30元,不高于60元.销售一段时间后发现:当销售单价为60元时,平均每月销售量为80件,而当销售单价每降低1元时,平均每月能多售出2件.同时,在销售过程中,每月还要支付其他费用450元.设销售单价为x元,平均月销售量为y件.
(1)求出y与x的函数关系式,并写出自变量x的取值范围.
(2)当销售单价为多少元时,销售这种童装平均每月可获利1 800元?
(3)当销售单价为多少元时,销售这种童装平均每月获得利润最大?最大利润是多少?
21.某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x … -3 - -2 -1 0 1 2
3 …
y … 3
m -1 0 -1 0
3 …
其中,m=__________.
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出两条函数的性质.
(4)进一步探究函数图象发现:
①函数图象与x轴有__________个交点,对应的方程x2-2|x|=0有__________
个实数根;
②方程x2-2|x|=2有__________个实数根;
③关于x的方程x2-2|x|=a有4个实数根时,a的取值范围是__________.
(第21题)
22.抛物线y=ax2+bx+c经过A(-1,0),B(4,0),C(0,3)三点,D为直线BC上方抛物线上一动点,DE⊥BC于E.
(第22题)
(1)求抛物线对应的函数表达式;
(2)如图①,求线段DE长度的最大值;
(3)如图②,设AB的中点为F,连结CD,CF.是否存在点D,使得△CDE中有一个角与∠CFO相等?若存在,求点D的横坐标;若不存在,请说明理由.
答案
一、1. B 2. A 3. B 4. B 5. C
6. C 7. B 8. D
9.D 点拨:设过点P且平行于直线y=x-2的直线的表达式为y=x+b,当直线y=x+b与抛物线只有一个交点P时,点P到直线y=x-2的距离最小,由
消去y得x2-4x+4-2b=0,
当Δ=0时,16-16+8b=0,
解得b=0,
∴直线的表达式为y=x.
如图,作OC⊥AB于点C,
设直线y=x-2交x轴于A,交y轴于B,则A(2,0),B(0,-2),
∴OA=OB=2,
∴AB=2 .
∵OC⊥AB,
∴OC=AB=.故选D.
(第9题)
10.A 点拨:①由抛物线可知:a>0,c<0,-<0,
∴b>0,
∴abc<0,故①正确;
②由对称轴可知:-=-1,
∴b=2a,
又∵x=1时,y=a+b+c=0,
∴c+3a=0,
∴c+2a=-3a+2a=-a<0,故②正确;
③点(1,0)关于直线x=-1的对称点为(-3,0),
∴x=-3时,y=9a-3b+c=0,故③正确;
④当x=-1时,y取最小值a-b+c,∴am2+bm+c≥a-b+c,
即a-b≤m(am+b),故④错误;
⑤抛物线与x轴有两个交点,
∴Δ>0,即b2-4ac>0,
∴4ac-b2<0,故⑤正确.故选A.
二、11.(答案不唯一)y=-x2+3
12. -7或5 13.-2
14.14 点拨:∵x=0和x=-2时y的值相同,都是0,
∴点和点关于二次函数图象的对称轴对称,
∴对称轴为直线x==-1.
∵横坐标为-3和1的点关于二次函数图象的对称轴对称,
∴x=-3时对应的函数值y=9,
∴9a-3b=9,
∴9a-3b+5=14.
15.2.25 m 点拨:因为水柱在与池中心的水平距离为1 m时达到最高,高度为3 m,
所以可设抛物线对应的函数表达式为y=a(x-1)2+3(0≤x≤3),把(3,0)代入得a=-,
所以y=-(x-1)2+3(0≤x≤3).
令x=0,则y==2.25,
即水管的长为2.25 m.
16. b-a 点拨:当x=c时,y=-2<0,
又∵当x=a和x=b时,y=0,抛物线开口向上,
∴a<c<b,则|a-c|+|c-b|=c-a+b-c=b-a.
三、17. 解:y=-3x2-6x+10=-3(x2+2x)+10=-3(x2+2x+1-1)+10=-3(x+1)2+13=-3[x-(-1)]2+13,
它的图象开口向下,对称轴为直线x=-1,顶点坐标为(-1,13).
18. 解:设二次函数的表达式为y=a(x-2)2+4,把(1,3)代入,得3=a+4,解得a=-1,
∴y=-(x-2)2+4=-x2+4x,
∴二次函数表达式为y=-x2+4x.
画出图象略.
19. 解:(1)把A(-2,1)的坐标代入y2=,得m=-2,
所以反比例函数的表达式为y2=-.
把B(1,n)的坐标代入y2=-,
得n=-2,所以B点坐标为(1,-2).把A(-2,1),B(1,-2)的坐标代入y1=ax2+c,得
解得
所以二次函数的表达式为y1=x2-3.
(2)观察图象可得,当y1>y2时,x<-2或x>0且x≠1.
20. 解:(1)由题意得y=80+2(60-x),
∴函数的关系式为y=-2x+200 (30≤x≤60).
(2)由题意得(x-30)(-2x+200)-450=1 800,解得x1=55,x2=75(不符合题意,舍去).
答:当销售单价为55元时,销售这种童装平均每月可获利1 800元.
(3)设每月获得的利润为w元,由题意得w=(x-30)(-2x+200)-450=-2(x-65)2+2 000.
∵-2<0,
∴当x≤65时,w随x的增大而增大.
又∵30≤x≤60,
∴当x=60时,w取最大值,w最大=-2×(60-65)2+2 000=1 950.
答:当销售单价为60元时,销售这种童装平均每月获得利润最大,最大利润是1 950元.
21. 解:(1)0 (2)如图.
(3)①函数y=x2-2|x|的图象关于y轴对称;②当x>1时,y随x的增大而增大.
(4)①3;3 ②2 ③-1
点拨:(3)题答案不唯一.
22. 解:(1)由题意得,解得
∴抛物线对应的函数表达式为y=-x2+x+3.
(2)设直线BC对应的函数表达式为y=kx+d,则解得
∴y=-x+3.
设D(m,-m2+m+3)(0<m<4).过点D作DM⊥x轴交BC于点M,则M,DM∥OC,
∴DM=-=-m2+3m,
∠DME=∠OCB,
又∵∠DEM=∠BOC=90°,
∴△DEM∽△BOC,
∴=.
∵OB=4,OC=3,
∴BC=5,
∴DE=DM,
∴DE=-m2+m=-(m-2)2+(0
(3)存在.
∵点F为AB的中点,
∴OF=,
∴tan∠CFO==2.
如图,过点B作BG⊥BC,交CD的延长线于G点,过点G作GH⊥x轴,垂足为H.
(第22题)
①若∠DCE=∠CFO,
则tan∠DCE==2,
∴BG=10.
易得△GBH∽△BCO,
∴==,
∴GH=8,BH=6,
∴G(10,8).
设直线CG对应的函数表达式为y=px+n,
∴解得
∴直线CG对应的函数表达式为y=x+3,
令x+3=-x2+x+3,
解得x=或x=0(舍去).
②若∠CDE=∠CFO,
同理可得BG=,GH=2,BH=,
∴G.
易得直线CG对应的函数表达式为y=-x+3,
令-x+3=-x2+x+3,
解得x=或x=0(舍去).
综上所述,点D的横坐标为或.
