人教版八年级上册数学11.1.1三角形的边课件(25张)
文档属性
| 名称 | 人教版八年级上册数学11.1.1三角形的边课件(25张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 613.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-04 00:00:00 | ||
图片预览



文档简介
第十一章
11.1.1三角形的边
1、了解三角形的基本概念;
2、理解三角形三边长的关系;
3、能结合具体的题目讨论三角形的三边关系。
学习目标
1.辨一辨:
下面是三根小棒摆成的图形,你认为哪些图形是三角形?
A B C D
C
A
B
D
H
B
E
F
G
(1) (2) (3)
(4)
(5)
2.说一说:什么叫三角形?
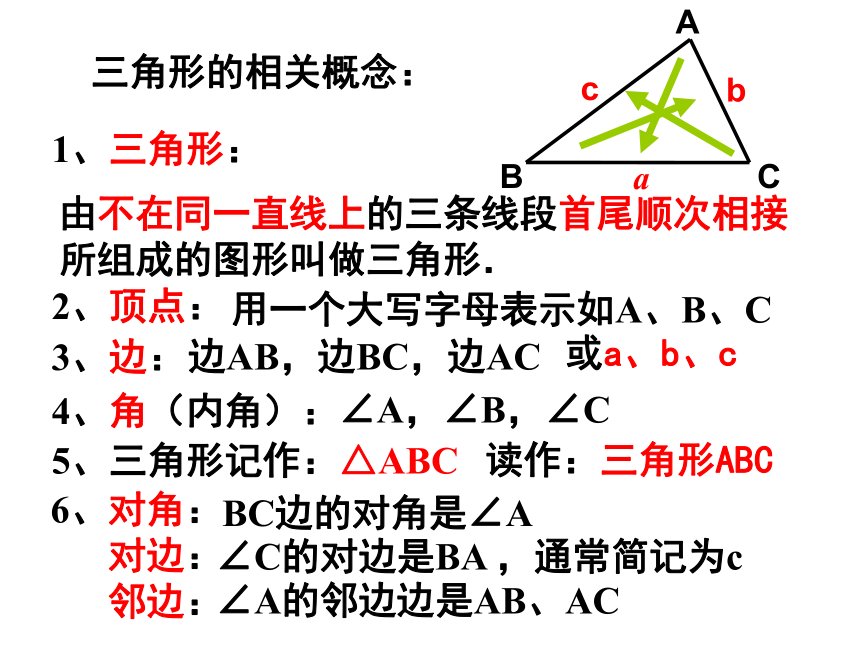
1、三角形:
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
2、顶点:
用一个大写字母表示如A、B、C
3、边:
边AB,边BC,边AC
4、角(内角):
∠A,∠B,∠C
5、三角形记作:△ABC
6、对角:
对边:
邻边:
三角形的相关概念:
∠C的对边是BA ,通常简记为c
BC边的对角是∠A
读作:三角形ABC
A
B
C
a
b
c
或a、b、c
∠A的邻边边是AB、AC
A
B
C
a
b
c
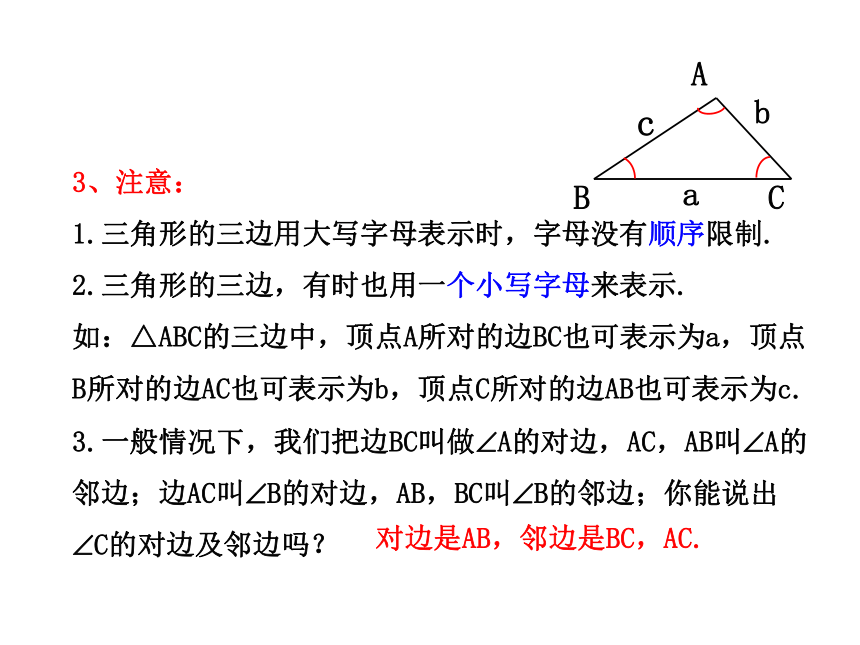
3、注意:
1.三角形的三边用大写字母表示时,字母没有顺序限制.
2.三角形的三边,有时也用一个小写字母来表示.
如:△ABC的三边中,顶点A所对的边BC也可表示为a,顶点B所对的边AC也可表示为b,顶点C所对的边AB也可表示为c.
3.一般情况下,我们把边BC叫做?A的对边,AC,AB叫?A的邻边;边AC叫?B的对边,AB,BC叫?B的邻边;你能说出?C的对边及邻边吗?
对边是AB,邻边是BC,AC.
A
D
C
B
E
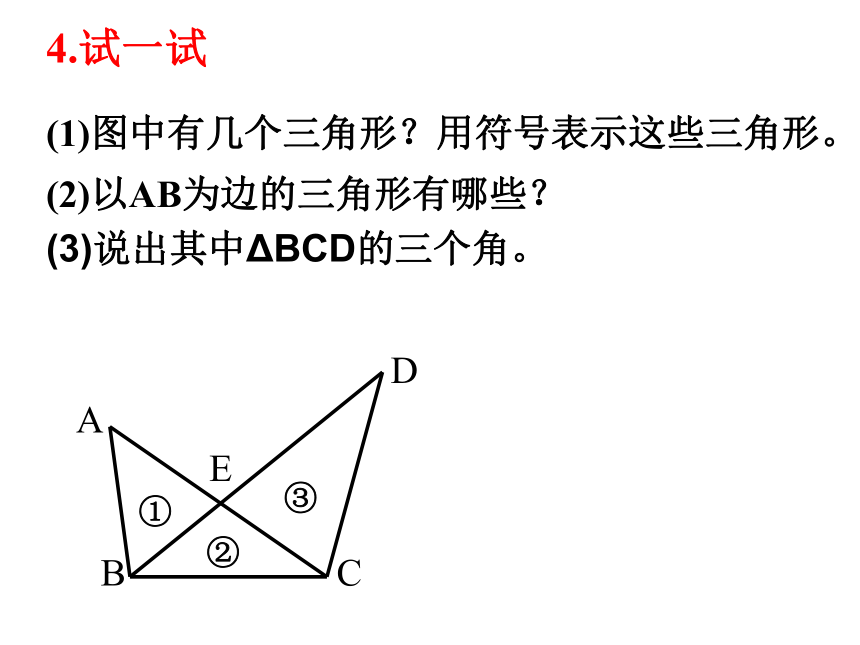
(1)图中有几个三角形?用符号表示这些三角形。
(2)以AB为边的三角形有哪些?
4.试一试
(3)说出其中ΔBCD的三个角。
①
②
③
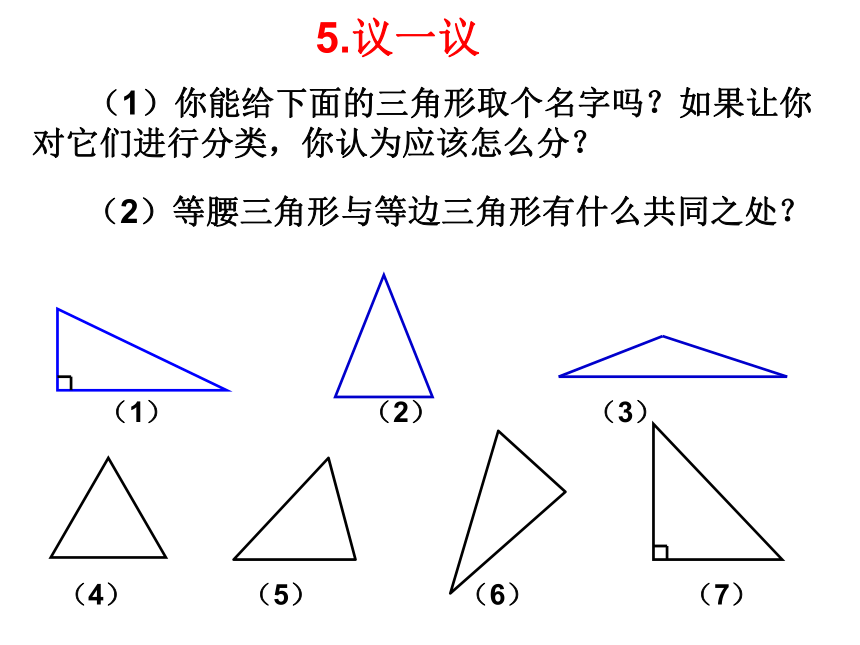
5.议一议
(1)你能给下面的三角形取个名字吗?如果让你对它们进行分类,你认为应该怎么分?
(2)等腰三角形与等边三角形有什么共同之处?
(1) (2) (3)
(4) (5) (6) (7)
直角三角形
锐角三角形
钝角三角形
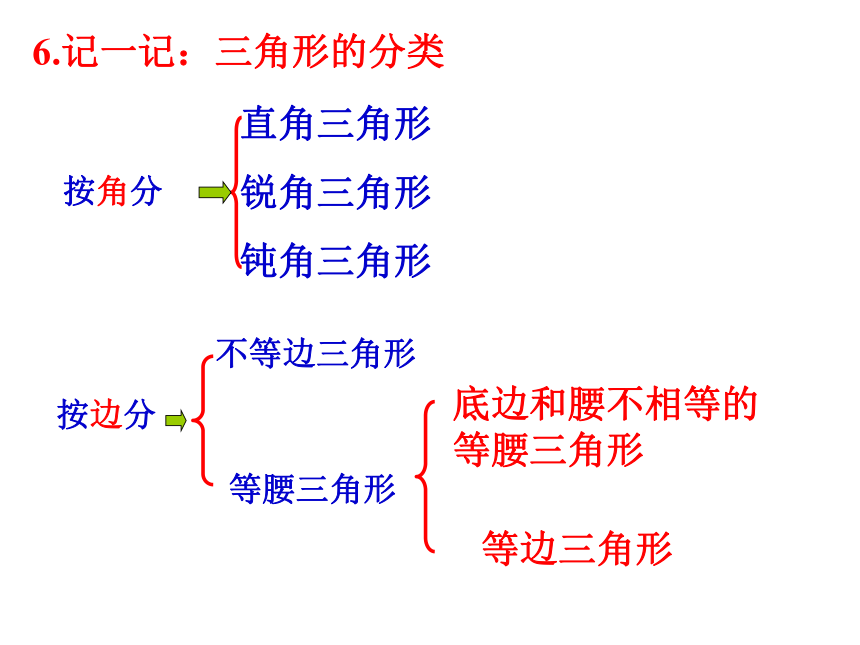
6.记一记:三角形的分类
不等边三角形
等腰三角形
按边分
按角分
底边和腰不相等的等腰三角形
等边三角形
三角形的分类
钝角三角形
直角三角形
锐角三角形
按角分
按边分
不等边三角形
等边三角形
等腰三角形
思考:三角形的三边长有没有什么特殊的关系呢?
B
A
C
教室
草坪
学校球场与教室之间隔着一块草坪, 有些同学不走校道而直接穿越草坪,时间久了,就会走出一条小路来,他们这样走对吗?如果不对,为什么还这样走?你能用学过的知识解释吗?
球场
校 道
C
A
B
AB+BC AC
AC+AB BC
BC+AC AB
8.探一探
结论:
两点之间,线段最短
三角形任意两边之和大于第三边
理由:
三角形的三边关系
C
A
B
a
b
c
即:在任意△ABC中有
a+b>c
b+c>a
a+c>b
(1)上面的三组小棒中, ②和 ③不能组成三角形,
能不能互换一根小棒,使两组小棒都能组成三角形?
9.练一练
只要满足较小的两条线段之和大于最长线段,
便可构成三角形;若不满足,则不能构成三角形。
.
三组小棒的长度:
① 13cm、7cm、10cm
② 6cm、14cm、 8cm
③ 5cm、9cm、16cm
思考:这三组小棒为什么有的能摆成三角形,有的不能?
(2)姚明说:“我一步能迈2.5米。”
你相信吗?
(注:姚明的腿长为1.2米。)
给出一个任意三角形,利用工具测量出这个三角形三边的长度。
计算测得三角形的任意两边之差,并与第三边比较,你能得到什么结论?
推论:三角形任何两边的差小于第三边
1、判断三条已知线段能否组成三角形:
小结:
若两条较短边的和大于最长边,
则可构成三角形,否则不能.
两边之差<第三边<两边之和
2、确定三角形第三边的取值范围:
已知一个等腰三角形,
1.若它的底边长为5cm,腰长为10cm,则它的周长为 。
2.若它的一边长为7cm,一边长为10cm,则它的周长为 。
3.若它的一边长为5cm,一边长为10cm,则它的周长为 。
②解:情况一:长为4cm的边是腰时,设底为 x cm
又因为4+4<10,所以不能围成腰长为4cm的等腰三角形。由以上讨论可知,三边长分别为4cm,7cm,7cm
解得:
情况二:长为4cm的边是底时,设腰为x cm
解得:
变式:用一根长为18厘米的细铁丝围成一个等腰三角形.
①如果腰长是底边的2倍,那么各边的长是多少?
②如果有一边的长为4cm,那么各边的长是多少?
要分类讨论
例2:在△ABC中,AC=5,BC=2, 并且AB是奇数。求△ABC的周长。
【分析】
根据确定三角形的三边关系有:
AC-BC < AB < AC+ BC
又根据已知条件AB是奇数
由以上两个条件可以得到线段AB的长
所以:△ABC的周长就可以求出
1、 在△ABC中,已知a=8cm,b=5cm,则c的取值范围是 ,
3cm16cm改:a=4cm,b=6cm.
a=2cm,b=7cm.
2cm,12cm5cm,14cm周长L的取值范围是 .
若c取奇数,则c= .
两边之差<第三边<两边之和
5cm,7cm,9cm,11cm
2.若△ABC的三边为a,b,c,则化简
︱a+b-c︱+︱b-a-c︱的结果是( ).
A. 2a-2b B.2a+2b+2c C. 2a D. 2a-2c
【解析】选C.根据三角形的三边关系得a+b-c>0,
b-a-c=b-(a+c)<0,所以原式=a+b-c-(b-a-c)
=a+b-c-b+a+c=2a.
2、现有两根木棒,它们的长度分别为20cm和30cm,若不改变木棒的长度, 要钉成一个三角形木架,应在下列四根木棒中选取 ( )
A.10cm的木棒 B.20cm的木棒 C.50cm的木棒 D.60cm的木棒
1、下列说法中,正确的有( )个:
A、4 B、3 C、2 D、1
(1)三角形可分为等腰三角形、钝角三角形、不等
边三角形。
(2)三角形可分为等边三角形和不等边三角形。
(3)三角形可分为等腰三角形和不等边三角形。
(4)等边三角形是特殊的等腰三角形。
一、选择题
一个等腰三角形的周长是20cm,若它的一条边长为5cm,求它的另两条边长。
1.有9, 8, 5, 3,的四根彩色线形木条,要摆出一个三角形,有 种摆法。
3.一个三角形有两条边相等,已知其中一边是3cm,另一边是9cm,则这个三角形的周长是______________
二、填空
三、解答题
2.一个等腰三角形的周长为5,如果它的三边长都是整数,那么它的各边长分别为____________.
三角形的概念
三角形的构成
三角形的表示
三角形的分类
三角形三边关系
注意:1.三角形的分类,要确定分类标准。
2.等腰三角形中的求边长及周长问题要注意分类讨论。
3.求三角形边长时,要用三边关系判断能否组成三角形。
(1)三条线段
(2)不在同一直线上
(3)首尾顺次相接
边、角、顶点
“△ABC”
按“边”分
按“角”分
两边之差<第三边<两边之和
知识梳理:
11.1.1三角形的边
1、了解三角形的基本概念;
2、理解三角形三边长的关系;
3、能结合具体的题目讨论三角形的三边关系。
学习目标
1.辨一辨:
下面是三根小棒摆成的图形,你认为哪些图形是三角形?
A B C D
C
A
B
D
H
B
E
F
G
(1) (2) (3)
(4)
(5)
2.说一说:什么叫三角形?
1、三角形:
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
2、顶点:
用一个大写字母表示如A、B、C
3、边:
边AB,边BC,边AC
4、角(内角):
∠A,∠B,∠C
5、三角形记作:△ABC
6、对角:
对边:
邻边:
三角形的相关概念:
∠C的对边是BA ,通常简记为c
BC边的对角是∠A
读作:三角形ABC
A
B
C
a
b
c
或a、b、c
∠A的邻边边是AB、AC
A
B
C
a
b
c
3、注意:
1.三角形的三边用大写字母表示时,字母没有顺序限制.
2.三角形的三边,有时也用一个小写字母来表示.
如:△ABC的三边中,顶点A所对的边BC也可表示为a,顶点B所对的边AC也可表示为b,顶点C所对的边AB也可表示为c.
3.一般情况下,我们把边BC叫做?A的对边,AC,AB叫?A的邻边;边AC叫?B的对边,AB,BC叫?B的邻边;你能说出?C的对边及邻边吗?
对边是AB,邻边是BC,AC.
A
D
C
B
E
(1)图中有几个三角形?用符号表示这些三角形。
(2)以AB为边的三角形有哪些?
4.试一试
(3)说出其中ΔBCD的三个角。
①
②
③
5.议一议
(1)你能给下面的三角形取个名字吗?如果让你对它们进行分类,你认为应该怎么分?
(2)等腰三角形与等边三角形有什么共同之处?
(1) (2) (3)
(4) (5) (6) (7)
直角三角形
锐角三角形
钝角三角形
6.记一记:三角形的分类
不等边三角形
等腰三角形
按边分
按角分
底边和腰不相等的等腰三角形
等边三角形
三角形的分类
钝角三角形
直角三角形
锐角三角形
按角分
按边分
不等边三角形
等边三角形
等腰三角形
思考:三角形的三边长有没有什么特殊的关系呢?
B
A
C
教室
草坪
学校球场与教室之间隔着一块草坪, 有些同学不走校道而直接穿越草坪,时间久了,就会走出一条小路来,他们这样走对吗?如果不对,为什么还这样走?你能用学过的知识解释吗?
球场
校 道
C
A
B
AB+BC AC
AC+AB BC
BC+AC AB
8.探一探
结论:
两点之间,线段最短
三角形任意两边之和大于第三边
理由:
三角形的三边关系
C
A
B
a
b
c
即:在任意△ABC中有
a+b>c
b+c>a
a+c>b
(1)上面的三组小棒中, ②和 ③不能组成三角形,
能不能互换一根小棒,使两组小棒都能组成三角形?
9.练一练
只要满足较小的两条线段之和大于最长线段,
便可构成三角形;若不满足,则不能构成三角形。
.
三组小棒的长度:
① 13cm、7cm、10cm
② 6cm、14cm、 8cm
③ 5cm、9cm、16cm
思考:这三组小棒为什么有的能摆成三角形,有的不能?
(2)姚明说:“我一步能迈2.5米。”
你相信吗?
(注:姚明的腿长为1.2米。)
给出一个任意三角形,利用工具测量出这个三角形三边的长度。
计算测得三角形的任意两边之差,并与第三边比较,你能得到什么结论?
推论:三角形任何两边的差小于第三边
1、判断三条已知线段能否组成三角形:
小结:
若两条较短边的和大于最长边,
则可构成三角形,否则不能.
两边之差<第三边<两边之和
2、确定三角形第三边的取值范围:
已知一个等腰三角形,
1.若它的底边长为5cm,腰长为10cm,则它的周长为 。
2.若它的一边长为7cm,一边长为10cm,则它的周长为 。
3.若它的一边长为5cm,一边长为10cm,则它的周长为 。
②解:情况一:长为4cm的边是腰时,设底为 x cm
又因为4+4<10,所以不能围成腰长为4cm的等腰三角形。由以上讨论可知,三边长分别为4cm,7cm,7cm
解得:
情况二:长为4cm的边是底时,设腰为x cm
解得:
变式:用一根长为18厘米的细铁丝围成一个等腰三角形.
①如果腰长是底边的2倍,那么各边的长是多少?
②如果有一边的长为4cm,那么各边的长是多少?
要分类讨论
例2:在△ABC中,AC=5,BC=2, 并且AB是奇数。求△ABC的周长。
【分析】
根据确定三角形的三边关系有:
AC-BC < AB < AC+ BC
又根据已知条件AB是奇数
由以上两个条件可以得到线段AB的长
所以:△ABC的周长就可以求出
1、 在△ABC中,已知a=8cm,b=5cm,则c的取值范围是 ,
3cm
a=2cm,b=7cm.
2cm
若c取奇数,则c= .
两边之差<第三边<两边之和
5cm,7cm,9cm,11cm
2.若△ABC的三边为a,b,c,则化简
︱a+b-c︱+︱b-a-c︱的结果是( ).
A. 2a-2b B.2a+2b+2c C. 2a D. 2a-2c
【解析】选C.根据三角形的三边关系得a+b-c>0,
b-a-c=b-(a+c)<0,所以原式=a+b-c-(b-a-c)
=a+b-c-b+a+c=2a.
2、现有两根木棒,它们的长度分别为20cm和30cm,若不改变木棒的长度, 要钉成一个三角形木架,应在下列四根木棒中选取 ( )
A.10cm的木棒 B.20cm的木棒 C.50cm的木棒 D.60cm的木棒
1、下列说法中,正确的有( )个:
A、4 B、3 C、2 D、1
(1)三角形可分为等腰三角形、钝角三角形、不等
边三角形。
(2)三角形可分为等边三角形和不等边三角形。
(3)三角形可分为等腰三角形和不等边三角形。
(4)等边三角形是特殊的等腰三角形。
一、选择题
一个等腰三角形的周长是20cm,若它的一条边长为5cm,求它的另两条边长。
1.有9, 8, 5, 3,的四根彩色线形木条,要摆出一个三角形,有 种摆法。
3.一个三角形有两条边相等,已知其中一边是3cm,另一边是9cm,则这个三角形的周长是______________
二、填空
三、解答题
2.一个等腰三角形的周长为5,如果它的三边长都是整数,那么它的各边长分别为____________.
三角形的概念
三角形的构成
三角形的表示
三角形的分类
三角形三边关系
注意:1.三角形的分类,要确定分类标准。
2.等腰三角形中的求边长及周长问题要注意分类讨论。
3.求三角形边长时,要用三边关系判断能否组成三角形。
(1)三条线段
(2)不在同一直线上
(3)首尾顺次相接
边、角、顶点
“△ABC”
按“边”分
按“角”分
两边之差<第三边<两边之和
知识梳理:
