人教版八年级上册数学12.1全等三角形的概念和性质课件(16张)
文档属性
| 名称 | 人教版八年级上册数学12.1全等三角形的概念和性质课件(16张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 25.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-04 00:00:00 | ||
图片预览




文档简介
全等三角形的概念与性质
教学目标:1.了解全等图形及全等三角形的概念.
2.理解全等三角形的性质.
看一看
能够完全重合
我们把能够完全重合的两个图形叫做 全等图形
形状、大小完全相同
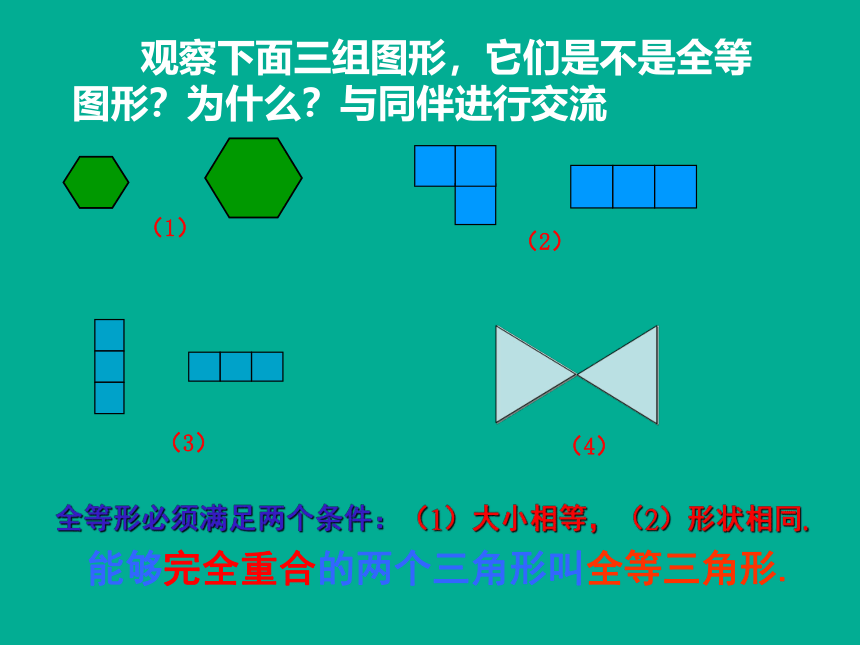
观察下面三组图形,它们是不是全等图形?为什么?与同伴进行交流
(1)
(2)
全等形必须满足两个条件:(1)大小相等,(2)形状相同.
(3)
能够完全重合的两个三角形叫全等三角形.
(4)
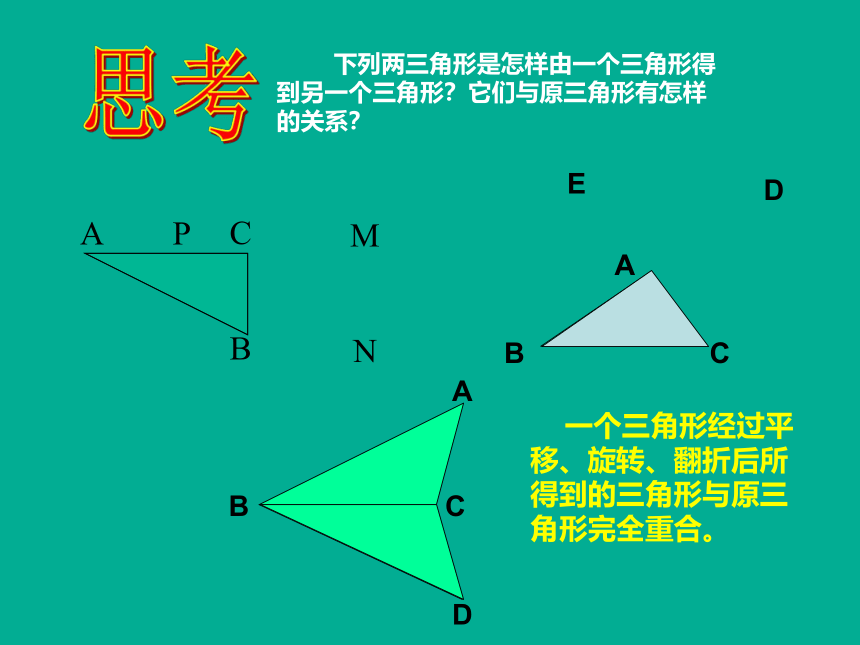
下列两三角形是怎样由一个三角形得到另一个三角形?它们与原三角形有怎样的关系?
思考
B
A
C
N
P
M
A
C
B
D
E
A
B
C
D
一个三角形经过平移、旋转、翻折后所得到的三角形与原三角形完全重合。
一、视频自主学习,回答问题。
1、 的两个图形叫做全等图形。
2、 的两个 叫做全等三角形。
3、全等用符号 表示,读作 。
4、在全等三角形中, 的顶点叫做对应顶点,
的 叫做对应边,能完全重合的角叫做
5、在表示两个三角形全等时,通常把表示对应顶点的字母
写在 位置上。
6、性质:全等三角形的
对应边 , 对应角 。
能够完全重合
能够完全重合
三角形
≌
全等于
能够完全重合
能够完全重合
边
对应角
相等
相等
对应
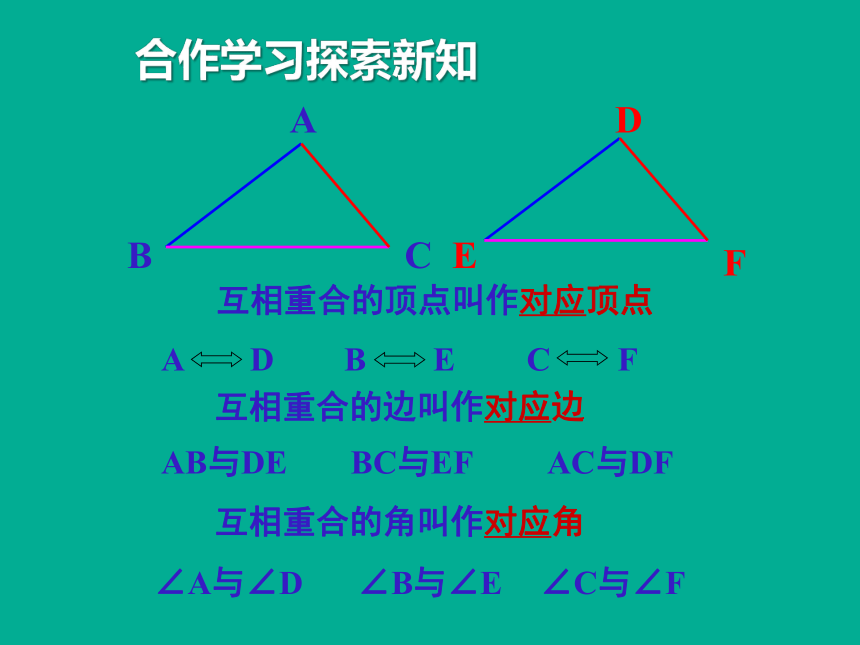
合作学习探索新知
A
B
C
E
D
F
互相重合的顶点叫作对应顶点
A D
B E
C F
互相重合的边叫作对应边
AB与DE
BC与EF
AC与DF
互相重合的角叫作对应角
∠A与∠D
∠B与∠E
∠C与∠F
A
B
C
E
D
F
记作:△ABC≌△DEF
注意:表示两个三角形全等时
一般要求把对应顶点的
字母写在对应的位置上.
“全等”用符号“ ”来表示,读作“ ”
≌
全等于
读作 :△ABC全等于△DEF
合作学习探索新知
全等三角形的对应边相等,全等三角形的对应角相等.
如图:∵△ABC≌ △DFE
∴ AB=DF, BC=FE, AC=DE(对应边相等)
几何语言:
∴∠A=∠D,∠B=∠F,∠C=∠E(对应角相等)
D
E
F
A
B
C
图形语言:
全等三角形的性质
举
例
例1 如图,已知△ABC≌△DCB,AB=3,DB=4,∠A=60°。
(1)写出△ABC和△DCB的对应边和对应角;
(2)求AC,DC的长及∠D的度数。
小组讨论
解(1)AB与DC,AC与DB,
BC与CB是对应边,
∠A与∠D,∠ABC与∠DCB,
∠ACB与∠DBC是对应角。
∴AC=DB=4,
DC=AB=3
(2)∵AC与DB,
AB与DC是全等三角形的对应边,
∵∠A与∠D是全等三角形的对应角,
∴∠D=∠A=60°
巩固练习
1.若△ABC≌△ A1B1C1,且∠A=110°, ∠B=40°,则∠C1= 度
2.已知△ABC≌△DEF, △ABC的周长为15,且AB=4,BC=5,则DF的长为 。
A1
A
B
C
B1
C1
30
6
D
A
B
C
E
F
3.如图所示,△ABC≌ △DEF,BE=4,AE=1,则DE的长是 。
4.已知:如图所示。△OAD ≌ △OBC,且∠O=70°,∠C=25°,则∠AEB= 度
A
B
F
C
E
D
O
B
C
D
E
A
5
120
互相重合的角叫做___
互相重合的边叫做____
其中:互相重合的顶点叫做___
2. 叫全等三角形。
1.能够重合的两个图形叫做 。
全等形
4.全等三角形的 和 相等
对应边
对应角
对应顶点
课堂小结
能够完全重合的两个三角形
3.“全等”用符号“ ”来表示,读作“ ”
对应边
对应角
5.书写全等式时要求把对应字母放在对应的位置上
全等于
≌
如图,已知△ AOC ≌ △BOD
求证:AC∥BD
拓展延伸、布置作业
教学目标:1.了解全等图形及全等三角形的概念.
2.理解全等三角形的性质.
看一看
能够完全重合
我们把能够完全重合的两个图形叫做 全等图形
形状、大小完全相同
观察下面三组图形,它们是不是全等图形?为什么?与同伴进行交流
(1)
(2)
全等形必须满足两个条件:(1)大小相等,(2)形状相同.
(3)
能够完全重合的两个三角形叫全等三角形.
(4)
下列两三角形是怎样由一个三角形得到另一个三角形?它们与原三角形有怎样的关系?
思考
B
A
C
N
P
M
A
C
B
D
E
A
B
C
D
一个三角形经过平移、旋转、翻折后所得到的三角形与原三角形完全重合。
一、视频自主学习,回答问题。
1、 的两个图形叫做全等图形。
2、 的两个 叫做全等三角形。
3、全等用符号 表示,读作 。
4、在全等三角形中, 的顶点叫做对应顶点,
的 叫做对应边,能完全重合的角叫做
5、在表示两个三角形全等时,通常把表示对应顶点的字母
写在 位置上。
6、性质:全等三角形的
对应边 , 对应角 。
能够完全重合
能够完全重合
三角形
≌
全等于
能够完全重合
能够完全重合
边
对应角
相等
相等
对应
合作学习探索新知
A
B
C
E
D
F
互相重合的顶点叫作对应顶点
A D
B E
C F
互相重合的边叫作对应边
AB与DE
BC与EF
AC与DF
互相重合的角叫作对应角
∠A与∠D
∠B与∠E
∠C与∠F
A
B
C
E
D
F
记作:△ABC≌△DEF
注意:表示两个三角形全等时
一般要求把对应顶点的
字母写在对应的位置上.
“全等”用符号“ ”来表示,读作“ ”
≌
全等于
读作 :△ABC全等于△DEF
合作学习探索新知
全等三角形的对应边相等,全等三角形的对应角相等.
如图:∵△ABC≌ △DFE
∴ AB=DF, BC=FE, AC=DE(对应边相等)
几何语言:
∴∠A=∠D,∠B=∠F,∠C=∠E(对应角相等)
D
E
F
A
B
C
图形语言:
全等三角形的性质
举
例
例1 如图,已知△ABC≌△DCB,AB=3,DB=4,∠A=60°。
(1)写出△ABC和△DCB的对应边和对应角;
(2)求AC,DC的长及∠D的度数。
小组讨论
解(1)AB与DC,AC与DB,
BC与CB是对应边,
∠A与∠D,∠ABC与∠DCB,
∠ACB与∠DBC是对应角。
∴AC=DB=4,
DC=AB=3
(2)∵AC与DB,
AB与DC是全等三角形的对应边,
∵∠A与∠D是全等三角形的对应角,
∴∠D=∠A=60°
巩固练习
1.若△ABC≌△ A1B1C1,且∠A=110°, ∠B=40°,则∠C1= 度
2.已知△ABC≌△DEF, △ABC的周长为15,且AB=4,BC=5,则DF的长为 。
A1
A
B
C
B1
C1
30
6
D
A
B
C
E
F
3.如图所示,△ABC≌ △DEF,BE=4,AE=1,则DE的长是 。
4.已知:如图所示。△OAD ≌ △OBC,且∠O=70°,∠C=25°,则∠AEB= 度
A
B
F
C
E
D
O
B
C
D
E
A
5
120
互相重合的角叫做___
互相重合的边叫做____
其中:互相重合的顶点叫做___
2. 叫全等三角形。
1.能够重合的两个图形叫做 。
全等形
4.全等三角形的 和 相等
对应边
对应角
对应顶点
课堂小结
能够完全重合的两个三角形
3.“全等”用符号“ ”来表示,读作“ ”
对应边
对应角
5.书写全等式时要求把对应字母放在对应的位置上
全等于
≌
如图,已知△ AOC ≌ △BOD
求证:AC∥BD
拓展延伸、布置作业
