牛顿第二定律课件42张PPT
图片预览




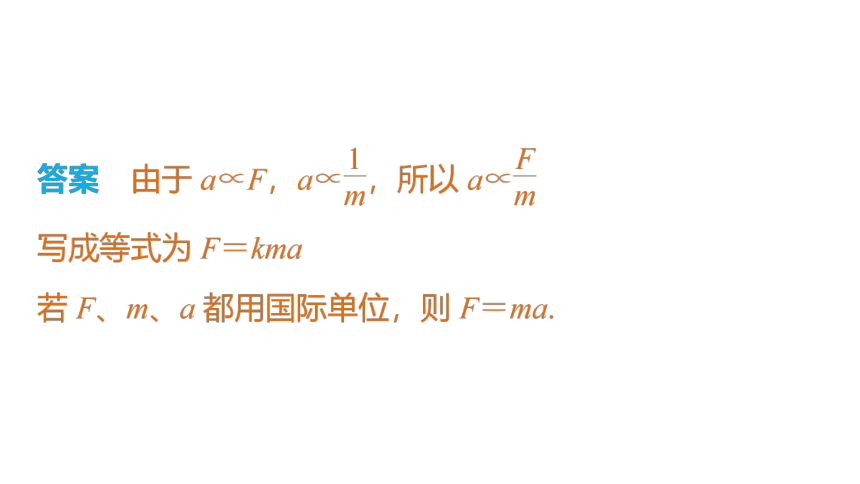







文档简介
第 三 章
牛顿运动定律
目标定位
1.知道牛顿第二定律的内容、表达式的确切含义.
2.知道国际单位制中力的单位“牛顿”是怎样定义的.
3.了解单位制的构成及力学中三个基本物理量在国际单位制中的单位.
4.能应用牛顿第二定律解决简单的实际问题.
学案3 牛顿第二定律
知识探究
自我检测
一、牛顿第二定律
知识探究
问题设计
要点提炼
1.牛顿第二定律
(1)内容:物体的加速度跟所受的合力成 ,跟物体的质量成 ,加速度的方向跟合力方向 .
(2)表达式
F=ma,式中各量都要用 单位,F指物体所受的 .
正比
反比
相同
国际
合外力
2.对牛顿第二定律的理解
(1)瞬时性:a与F同时产生,同时 ,同时 ,为瞬时对应关系.
(2)矢量性:F=ma是矢量表达式,任一时刻a的方向均与__
的方向一致,当合外力方向变化时a的方向同时变化,即a与F的方向在任何时刻均 .
(3)同体性:公式F=ma中各物理量都是针对 的.
变化
消失
合
外力F
相同
同一物体
(4)独立性:当物体同时受到几个力作用时,各个力都满足F=ma,每个力都会产生一个加速度,这些加速度的矢量和即为物体具有的 ,故牛顿第二定律可表示为
3.合外力、加速度、速度的关系
(1)力与加速度为因果关系.力是因,加速度是果.只要物体受到的合外力不为零,就产生加速度.加速度的方向与合外力方向总 、大小与合外力成 .
合加速度
相同
正比
(2)力与速度无因果关系.合外力方向与速度方向可以同向,可以反向;合外力方向与速度方向 时,物体做加速运动, 时物体做减速运动.
同向
反向
无关
1.解题步骤
(1)确定研究对象.
(2)进行受力分析和运动情况分析,作出受力和运动示意图.
(3)求合力F或加速度a.
(4)根据F=ma列方程求解.
二、牛顿第二定律的简单应用
2.解题方法
(1)矢量合成法:若物体只受两个力作用时,应用平行四边形定则求这两个力的合力,加速度的方向与物体所受合外力的方向相同.
(2)正交分解法:当物体受多个力作用时,常用正交分解法求物体的合外力.
①建立坐标系时,通常选取加速度的方向作为某一坐标轴的正方向(也就是不分解加速度),将物体所受的力正交分解后,列出方程Fx=ma,Fy=0.
②特殊情况下,若物体的受力都在两个互相垂直的方向上,也可将坐标轴建立在力的方向上,正交分解加速度a.根据牛顿第二定律 列方程及F= 求合外力.
问题设计
美国国家航空航天局(NASA)在20世纪末曾发射过一个火星探测器,但它由于靠火星过近,结果因温度过高而起火,并脱离轨道坠入火星的大气层.航空航天局调查事故原因时发现:原来探测器的制造商洛克希德·马丁公司计算加速度时使用了英制单位,而喷气推动实验室的工程师理所当然地认为他们提供的数据是以国际单位制算出来的,并把这些数据直接输入电脑.从这次事故的原因上,你能得到什么启示?
三、力学单位制
答案 在国际上采用统一的单位制是非常重要的,也是非常必要的.
1.单位制
(1)基本单位:物理公式在确定物理量的数量关系的同时,也确定了物理量的 关系.在物理学中,选定几个物理量的单位作为基本单位.
(2)导出单位:根据物理公式中其他物理量和这几个物理量的关系,导出来的单位叫 .
(3)单位制: 和 一起组成了单位制.
要点提炼
单位
导出单位
基本单位
导出单位
2.国际单位制中的力学单位
(1)基本单位
长度l,单位: ;质量m,单位: ;时间t,单位: .
(2)常用的导出单位
速度(v),由公式v= 导出,单位: .
加速度(a),由公式a= 导出,单位: .
力(F),由公式 导出,单位: .
此外还有功、功率、压强等.
m
kg
s
m/s
m/s2
F=ma
N(或kg·m/s2)
3.单位制在计算中的应用
(1)单位制可以简化计算过程
计算时首先将各物理量的单位统一到国际单位制中,这样就可以省去计算过程中单位的代入,只在数字后面写上相应待求量的单位即可,从而使计算简便.
(2)单位制可检查物理量关系式的正误
根据物理量的单位,如果发现某公式在单位上有问题,或者所求结果的单位与采用的单位制中该量的单位不一致,那么该公式或计算结果肯定是错误的.
典例精析
一、对牛顿第二定律的理解
例1 下列对牛顿第二定律的表达式F=ma及其变形公式的理解,正确的是( )
A.由F=ma可知,物体所受的合外力与物体的质量成正比,与物体的加速度成反比
B.由m= 可知,物体的质量与其所受合外力成正比,与其运动的加速度成反比
答案 CD
二、牛顿第二定律的应用
例2 如图1所示,一质量为8 kg的物体静止在粗糙的水平地面上,物体与地面间的动摩擦因数为0.2,用一水平力F=20 N拉物体由A点开始运动,经过8 s后撤去拉力F,再经过一段时间物体到达B点停止.求:(g=10 m/s2)
图1
(1)在拉力F作用下物体运动的加速度大小;
解析 对物体受力分析,如图所示
竖直方向mg=N
水平方向,由牛顿第二定律得
F-μN=ma1
答案 0.5 m/s2
(2)撤去拉力时物体的速度大小;
解析 撤去拉力时物体的速度v=a1t
解得v=4 m/s
答案 4 m/s
(3)撤去拉力F后物体运动的距离.
解析 撤去拉力F后由牛顿第二定律得
-μmg=ma2
解得a2=-μg=-2 m/s2
由0-v2=2a2x
答案 4 m
例3 一质量为103 t的列车,机车牵引力为3.5×105 N,运动中所受阻力为车重的0.01倍.列车由静止开始做匀加速直线运动,速度变为180 km/h需多长时间?此过程中前进了多远距离?(g取10 m/s2)
解析 列车质量m=103 t=106 kg,
重力G=mg=106×10 N=107 N,
三、单位制在计算中的应用
运动中所受阻力
f=0.01G=0.01×107 N=105 N.
设列车匀加速运动的加速度为a.
由牛顿第二定律得
F牵-f=ma,
列车由静止加速到v=180 km/h=50 m/s所用时间为
答案 200 s 5 km
课堂要点小结
1.牛顿第二定律和力的单位
(1)内容
(2)表达式:F=ma
(3)国际单位制中力的单位:N,1 N=1 kg·m/s2
2.牛顿第二定律的特点
(1)瞬时性;(2)矢量性;(3)同体性;(4)独立性.
课堂要点小结
3.应用牛顿第二定律解题的一般步骤和基本方法
一般步骤:(1)确定研究对象;
(2)进行受力分析和运动情况分析;
(3)求出合外力或加速度;
(4)根据牛顿第二定律F=ma列方程求解.
课堂要点小结
基本方法:
(1)两个力作用时可用矢量合成法,也可用正交分解法;
(2)多个力作用时可用正交分解法.
4.力学单位制
(1)单位制
①基本单位:基本物理量的单位.
课堂要点小结
②导出单位:由基本物理量根据物理关系推导出来的其他物理量的单位.
(2)国际单位制中的力学单位有:长度的单位米(m),时间的单位秒(s),质量的单位千克(kg).
自我检测
1.(牛顿第二定律的理解)从匀速上升的气球上释放一物体,在释放的瞬间,物体相对地面将具有( )
A.向上的速度 B.向下的速度
C.向上的加速度 D.向下的加速度
1
2
3
1
2
3
在释放的瞬间,物体和气球具有相同的速度,A正确,B错误.
答案 AD
2.(单位制的应用)一物体在2 N的外力作用下,产生10 cm/s2的加速度,求该物体的质量.下面有几种不同的求法,其中单位运用正确、简洁而又规范的是( )
1
2
3
1
2
3
解析 带单位运算时,每一个数据均要带上单位,且单位换算要准确,也可以把题中的已知量的单位都用国际单位表示,计算所得结果的单位就是国际单位,这样在统一已知量的单位后,就不必再一一写出各个量的单位,只在数
字后面写出正确单位即可.在备选的四个选项中A、C均错,B项解题过程正确,但不简洁,只有D项单位运用正确,且简洁而又规范.
答案 D
1
2
3
3.(牛顿第二定律的简单应用)如图2所示,沿水平方向做匀变速直线运动的车厢中,悬挂小球的悬线偏离竖直方向37°角,小球和车厢相对静止,小球的质量为1 kg.(g取10 m/s2,sin 37°=0.6,cos 37°=0.8)
图2
1
2
3
(1)求车厢运动的加速度并说明车厢的运动情况;
解析 解法一(合成法)
小球和车厢相对静止,它们的加速度相同.以小球为研究对象,对小球进行受力分析如图所示,小球所受合力为F合=mgtan 37°.
1
2
3
1
2
3
1
2
3
解法二(正交分解法)
建立直角坐标系如图所示,正交分解各力,根据牛顿第二定律列方程得
x方向:Tx=ma
y方向:Ty-mg=0
即Tsin 37°=ma
Tcos 37°-mg=0
1
2
3
加速度方向水平向右.车厢的加速度与小球相同,车厢做的是向右的匀加速直线运动或向左的匀减速直线运动.
答案 7.5 m/s2,方向水平向右 车厢可能向右做匀加速直线运动或向左做匀减速直线运动
1
2
3
(2)求悬线对球的拉力大小.
解析 解法一(合成法)
由图可知,悬线对小球的拉力大小为
解法二(正交分解法)
由(1)中所列方程解得悬线对小球的拉力大小为
答案 12.5 N
牛顿运动定律
目标定位
1.知道牛顿第二定律的内容、表达式的确切含义.
2.知道国际单位制中力的单位“牛顿”是怎样定义的.
3.了解单位制的构成及力学中三个基本物理量在国际单位制中的单位.
4.能应用牛顿第二定律解决简单的实际问题.
学案3 牛顿第二定律
知识探究
自我检测
一、牛顿第二定律
知识探究
问题设计
要点提炼
1.牛顿第二定律
(1)内容:物体的加速度跟所受的合力成 ,跟物体的质量成 ,加速度的方向跟合力方向 .
(2)表达式
F=ma,式中各量都要用 单位,F指物体所受的 .
正比
反比
相同
国际
合外力
2.对牛顿第二定律的理解
(1)瞬时性:a与F同时产生,同时 ,同时 ,为瞬时对应关系.
(2)矢量性:F=ma是矢量表达式,任一时刻a的方向均与__
的方向一致,当合外力方向变化时a的方向同时变化,即a与F的方向在任何时刻均 .
(3)同体性:公式F=ma中各物理量都是针对 的.
变化
消失
合
外力F
相同
同一物体
(4)独立性:当物体同时受到几个力作用时,各个力都满足F=ma,每个力都会产生一个加速度,这些加速度的矢量和即为物体具有的 ,故牛顿第二定律可表示为
3.合外力、加速度、速度的关系
(1)力与加速度为因果关系.力是因,加速度是果.只要物体受到的合外力不为零,就产生加速度.加速度的方向与合外力方向总 、大小与合外力成 .
合加速度
相同
正比
(2)力与速度无因果关系.合外力方向与速度方向可以同向,可以反向;合外力方向与速度方向 时,物体做加速运动, 时物体做减速运动.
同向
反向
无关
1.解题步骤
(1)确定研究对象.
(2)进行受力分析和运动情况分析,作出受力和运动示意图.
(3)求合力F或加速度a.
(4)根据F=ma列方程求解.
二、牛顿第二定律的简单应用
2.解题方法
(1)矢量合成法:若物体只受两个力作用时,应用平行四边形定则求这两个力的合力,加速度的方向与物体所受合外力的方向相同.
(2)正交分解法:当物体受多个力作用时,常用正交分解法求物体的合外力.
①建立坐标系时,通常选取加速度的方向作为某一坐标轴的正方向(也就是不分解加速度),将物体所受的力正交分解后,列出方程Fx=ma,Fy=0.
②特殊情况下,若物体的受力都在两个互相垂直的方向上,也可将坐标轴建立在力的方向上,正交分解加速度a.根据牛顿第二定律 列方程及F= 求合外力.
问题设计
美国国家航空航天局(NASA)在20世纪末曾发射过一个火星探测器,但它由于靠火星过近,结果因温度过高而起火,并脱离轨道坠入火星的大气层.航空航天局调查事故原因时发现:原来探测器的制造商洛克希德·马丁公司计算加速度时使用了英制单位,而喷气推动实验室的工程师理所当然地认为他们提供的数据是以国际单位制算出来的,并把这些数据直接输入电脑.从这次事故的原因上,你能得到什么启示?
三、力学单位制
答案 在国际上采用统一的单位制是非常重要的,也是非常必要的.
1.单位制
(1)基本单位:物理公式在确定物理量的数量关系的同时,也确定了物理量的 关系.在物理学中,选定几个物理量的单位作为基本单位.
(2)导出单位:根据物理公式中其他物理量和这几个物理量的关系,导出来的单位叫 .
(3)单位制: 和 一起组成了单位制.
要点提炼
单位
导出单位
基本单位
导出单位
2.国际单位制中的力学单位
(1)基本单位
长度l,单位: ;质量m,单位: ;时间t,单位: .
(2)常用的导出单位
速度(v),由公式v= 导出,单位: .
加速度(a),由公式a= 导出,单位: .
力(F),由公式 导出,单位: .
此外还有功、功率、压强等.
m
kg
s
m/s
m/s2
F=ma
N(或kg·m/s2)
3.单位制在计算中的应用
(1)单位制可以简化计算过程
计算时首先将各物理量的单位统一到国际单位制中,这样就可以省去计算过程中单位的代入,只在数字后面写上相应待求量的单位即可,从而使计算简便.
(2)单位制可检查物理量关系式的正误
根据物理量的单位,如果发现某公式在单位上有问题,或者所求结果的单位与采用的单位制中该量的单位不一致,那么该公式或计算结果肯定是错误的.
典例精析
一、对牛顿第二定律的理解
例1 下列对牛顿第二定律的表达式F=ma及其变形公式的理解,正确的是( )
A.由F=ma可知,物体所受的合外力与物体的质量成正比,与物体的加速度成反比
B.由m= 可知,物体的质量与其所受合外力成正比,与其运动的加速度成反比
答案 CD
二、牛顿第二定律的应用
例2 如图1所示,一质量为8 kg的物体静止在粗糙的水平地面上,物体与地面间的动摩擦因数为0.2,用一水平力F=20 N拉物体由A点开始运动,经过8 s后撤去拉力F,再经过一段时间物体到达B点停止.求:(g=10 m/s2)
图1
(1)在拉力F作用下物体运动的加速度大小;
解析 对物体受力分析,如图所示
竖直方向mg=N
水平方向,由牛顿第二定律得
F-μN=ma1
答案 0.5 m/s2
(2)撤去拉力时物体的速度大小;
解析 撤去拉力时物体的速度v=a1t
解得v=4 m/s
答案 4 m/s
(3)撤去拉力F后物体运动的距离.
解析 撤去拉力F后由牛顿第二定律得
-μmg=ma2
解得a2=-μg=-2 m/s2
由0-v2=2a2x
答案 4 m
例3 一质量为103 t的列车,机车牵引力为3.5×105 N,运动中所受阻力为车重的0.01倍.列车由静止开始做匀加速直线运动,速度变为180 km/h需多长时间?此过程中前进了多远距离?(g取10 m/s2)
解析 列车质量m=103 t=106 kg,
重力G=mg=106×10 N=107 N,
三、单位制在计算中的应用
运动中所受阻力
f=0.01G=0.01×107 N=105 N.
设列车匀加速运动的加速度为a.
由牛顿第二定律得
F牵-f=ma,
列车由静止加速到v=180 km/h=50 m/s所用时间为
答案 200 s 5 km
课堂要点小结
1.牛顿第二定律和力的单位
(1)内容
(2)表达式:F=ma
(3)国际单位制中力的单位:N,1 N=1 kg·m/s2
2.牛顿第二定律的特点
(1)瞬时性;(2)矢量性;(3)同体性;(4)独立性.
课堂要点小结
3.应用牛顿第二定律解题的一般步骤和基本方法
一般步骤:(1)确定研究对象;
(2)进行受力分析和运动情况分析;
(3)求出合外力或加速度;
(4)根据牛顿第二定律F=ma列方程求解.
课堂要点小结
基本方法:
(1)两个力作用时可用矢量合成法,也可用正交分解法;
(2)多个力作用时可用正交分解法.
4.力学单位制
(1)单位制
①基本单位:基本物理量的单位.
课堂要点小结
②导出单位:由基本物理量根据物理关系推导出来的其他物理量的单位.
(2)国际单位制中的力学单位有:长度的单位米(m),时间的单位秒(s),质量的单位千克(kg).
自我检测
1.(牛顿第二定律的理解)从匀速上升的气球上释放一物体,在释放的瞬间,物体相对地面将具有( )
A.向上的速度 B.向下的速度
C.向上的加速度 D.向下的加速度
1
2
3
1
2
3
在释放的瞬间,物体和气球具有相同的速度,A正确,B错误.
答案 AD
2.(单位制的应用)一物体在2 N的外力作用下,产生10 cm/s2的加速度,求该物体的质量.下面有几种不同的求法,其中单位运用正确、简洁而又规范的是( )
1
2
3
1
2
3
解析 带单位运算时,每一个数据均要带上单位,且单位换算要准确,也可以把题中的已知量的单位都用国际单位表示,计算所得结果的单位就是国际单位,这样在统一已知量的单位后,就不必再一一写出各个量的单位,只在数
字后面写出正确单位即可.在备选的四个选项中A、C均错,B项解题过程正确,但不简洁,只有D项单位运用正确,且简洁而又规范.
答案 D
1
2
3
3.(牛顿第二定律的简单应用)如图2所示,沿水平方向做匀变速直线运动的车厢中,悬挂小球的悬线偏离竖直方向37°角,小球和车厢相对静止,小球的质量为1 kg.(g取10 m/s2,sin 37°=0.6,cos 37°=0.8)
图2
1
2
3
(1)求车厢运动的加速度并说明车厢的运动情况;
解析 解法一(合成法)
小球和车厢相对静止,它们的加速度相同.以小球为研究对象,对小球进行受力分析如图所示,小球所受合力为F合=mgtan 37°.
1
2
3
1
2
3
1
2
3
解法二(正交分解法)
建立直角坐标系如图所示,正交分解各力,根据牛顿第二定律列方程得
x方向:Tx=ma
y方向:Ty-mg=0
即Tsin 37°=ma
Tcos 37°-mg=0
1
2
3
加速度方向水平向右.车厢的加速度与小球相同,车厢做的是向右的匀加速直线运动或向左的匀减速直线运动.
答案 7.5 m/s2,方向水平向右 车厢可能向右做匀加速直线运动或向左做匀减速直线运动
1
2
3
(2)求悬线对球的拉力大小.
解析 解法一(合成法)
由图可知,悬线对小球的拉力大小为
解法二(正交分解法)
由(1)中所列方程解得悬线对小球的拉力大小为
答案 12.5 N
同课章节目录
- 第一章 运动的描述
- 1 质点 参考系 空间 时间
- 2 位置变化的描述——位移
- 3 运动快慢与方向的描述——速度
- 4 速度变化快慢的描述——加速度
- 5 匀变速直线运动速度与时间的关系
- 6 匀变速直线运动位移与时间的关系
- 7 对自由落体运动的研究
- 8 匀变速直线运动规律的应用
- 9 测定匀变速直线运动的加速度
- 第二章 力
- 1 力
- 2 重力
- 3 弹力
- 4 摩擦力
- 5 力的合成
- 6 力的分解
- 第三章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿第三定律
- 5 牛顿运动定律的应用
- 6 超重与失重
- 第四章 物体的平衡
- 1 共点力作用下物体的平衡
- 2 共点力平衡条件的应用
- 3 平衡的稳定性(选学)
