人教版数学九年级上册21.2.1 第2课时 用配方法解一元二次方程课件(20张)
文档属性
| 名称 | 人教版数学九年级上册21.2.1 第2课时 用配方法解一元二次方程课件(20张) |  | |
| 格式 | ppt | ||
| 文件大小 | 433.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-02 19:15:12 | ||
图片预览








文档简介
第2课时 用配方法解一元二次方程
一、教学目标
1.掌握配方法和指导过程,能使用配方法解一元二次方程.
2.通过降次的思想解方程,掌握一些转化的技能.
重点
难点
二、教学重难点
配方法的解题步骤.
用配方法解系数不为1的一元二次方程.
活动1 新课导入
三、教学设计
1.填空:
(1) x2+6x+____=(x+____)2 ;
9
3
2.若x2-mx+64是一个完全平方式,则m的值是____.
±16
活动2 探究新知
探 究
怎样解方程 x2+6x+4=0?
我们已经会解方程(x+3)?=5.因为它的左边是含有x的完全平方式,右边是非负数,所以可以直接降次解方程.那么,能否将方程x2+6x+4=0转化为可以直接降次的形式再求解呢?
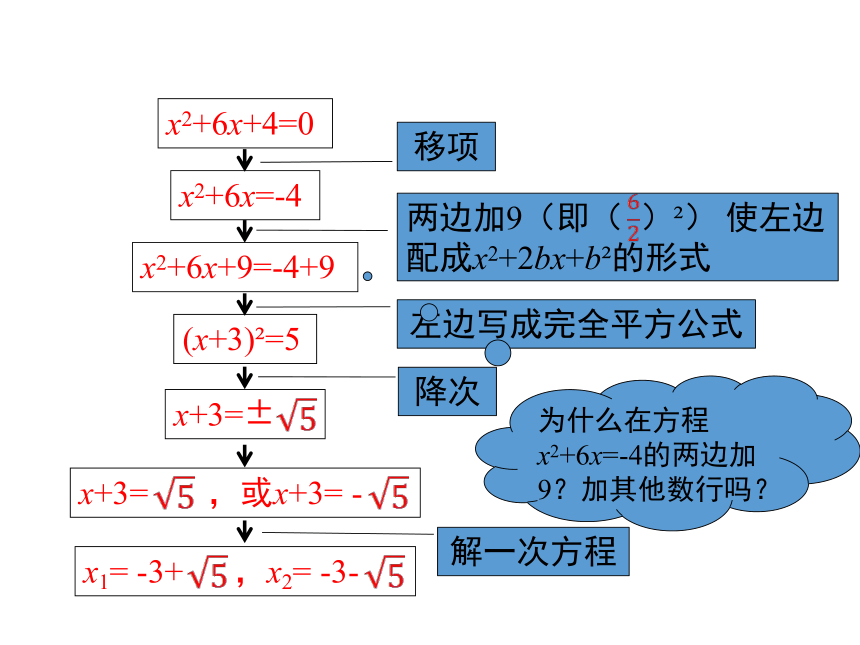
解方程x2+6x+4=0的过程可以用下面的框图表示:
x2+6x+4=0
x2+6x=-4
x2+6x+9=-4+9
(x+3)?=5
x+3=±
x+3= ,或x+3= -
x1= -3+ ,x2= -3-
移项
两边加9(即( )?) 使左边配成x2+2bx+b?的形式
左边写成完全平方公式
降次
解一次方程
为什么在方程x2+6x=-4的两边加9?加其他数行吗?
可以验证,-3± 是方程x2+6x+4=0的两个根。
像上面那样,通过配成完全平方形式来解一元二次方程的方法,叫做配方法。可以看出,配方是为了降次,把一个一元二次方程转化成两个一元二次方程来解。
提出问题:
(1)请把方程(x+3)2=5化成一般形式,然后与所探究中的方程进行比较,你有什么发现?
(2)如何将方程x2+6x+4=0化成(x+3)2=5的形式呢?
(3)把常数项移到方程右边之后,为什么要在x2+6x=-4的两边都加上9?加其他数行吗?
(4)通过x2+6x+4=0的解题过程,你能说说配方的一般步骤是什么吗?配方的关键是什么吗?
2.解方程3x2-2x-1=0.
提出问题:
(1)如果一个一元二次方程的二次项系数不为1,还能用配方法来解吗?
(2)请将方程3x2-2x-1=0的二次项系数化为1,并尝试解此方程;
(3)由此请你再归纳一下用配方法解一元二次方程的一般步骤.
活动3 知识归纳
1.通过配成________形式来解一元二次方程的方法,叫做配方法.
2.对于任意一元二次方程,用配方法解的一般步骤:①先化成________;②将常数项移到等式右边;③两边除以__________;④方程两边都加上____________
________;⑤将等式左边化成_____________;⑥两边开方,并求出方程的解.
完全平方
一般形式
二次项系数
一次项系数一
半的平方
完全平方形式
提出问题:
(1)配方过程中,在等式两边加上的常数与一次项系数的关系如何?
(2)配方过程中,若等号右边为负数,这个方程有没有实数根?
(3)配方过程中还需注意哪些问题?
活动4 例题与练习
例1.解下列方程:
(1)x2-8x+1=0;(2)2x2+1=3x; (3)3x2-6x+4=0
分析:(1)方程的二次项系数为1,直接运用配方法.
(2)先把方程化成2x2-3x+1=0.它的二次项系数为2,为了便于配方,需将二次项系数化为1,为此方程的两边都除以2.
(3)与(2)类似,方程的两边都除以3后再配方.
解:(1)移项,得
x2-8x=-1,
配方,得
x2-8x+42=-1+42 ,
( x-4)2=15
由此可得
即
配方,得
由此可得
二次项系数化为1,得
解:移项,得
2x2-3x=-1,
即
配方,得
解:移项,得
二次项系数化为1,得
即
因为实数的平方不会是负数,所以x取任何实数时,(x-1)?都是非负数,上式都不成立,即原方程无实数根。
例2 求证:无论x为何值,代数式2x2-4x+3的值恒大于0.
证明:2x2-4x+3
=
=
= 2(x-1)2+1.
∵(x-1)2≥0,∴2(x-1)2+1>0,
∴无论x为何值,代数式2x2-4x+3的值恒大于0.
提出问题:
二次三项式的配方与一元二次方程的配方有什么区别,请指出具体区别在什么地方?
二次三项式配方时,不能除以二次项的系数,只能提取二次项的系数,并添上括号,再用配方法构造一个完全平方式;而一元二次方程配方时,两边除以二次项系数后,再用配方法构造一个完全平方式.
练 习
1.教材P9 练习第1,2题.
2.代数式x2-8x+18的值( )
A.恒为正 B.恒为负
C.可能为0 D.不能确定
3.把方程2x2+6x-1=0配方后得(x+m)2=k,则m=____,k=____.
A
4.式子-x2-4x-5,可配方为-(x+____)2____,该式有最____值,是____.
5.试证明:无论a为何实数,关于x的方程(a2-8a+17)x2+2ax+1=0都是一元二次方程.
证明:∵a2-8a+17=(a-4)2+1>0,
∴无论a为何实数,该方程都是一元二次方程.
2
-1
大
-1
一、教学目标
1.掌握配方法和指导过程,能使用配方法解一元二次方程.
2.通过降次的思想解方程,掌握一些转化的技能.
重点
难点
二、教学重难点
配方法的解题步骤.
用配方法解系数不为1的一元二次方程.
活动1 新课导入
三、教学设计
1.填空:
(1) x2+6x+____=(x+____)2 ;
9
3
2.若x2-mx+64是一个完全平方式,则m的值是____.
±16
活动2 探究新知
探 究
怎样解方程 x2+6x+4=0?
我们已经会解方程(x+3)?=5.因为它的左边是含有x的完全平方式,右边是非负数,所以可以直接降次解方程.那么,能否将方程x2+6x+4=0转化为可以直接降次的形式再求解呢?
解方程x2+6x+4=0的过程可以用下面的框图表示:
x2+6x+4=0
x2+6x=-4
x2+6x+9=-4+9
(x+3)?=5
x+3=±
x+3= ,或x+3= -
x1= -3+ ,x2= -3-
移项
两边加9(即( )?) 使左边配成x2+2bx+b?的形式
左边写成完全平方公式
降次
解一次方程
为什么在方程x2+6x=-4的两边加9?加其他数行吗?
可以验证,-3± 是方程x2+6x+4=0的两个根。
像上面那样,通过配成完全平方形式来解一元二次方程的方法,叫做配方法。可以看出,配方是为了降次,把一个一元二次方程转化成两个一元二次方程来解。
提出问题:
(1)请把方程(x+3)2=5化成一般形式,然后与所探究中的方程进行比较,你有什么发现?
(2)如何将方程x2+6x+4=0化成(x+3)2=5的形式呢?
(3)把常数项移到方程右边之后,为什么要在x2+6x=-4的两边都加上9?加其他数行吗?
(4)通过x2+6x+4=0的解题过程,你能说说配方的一般步骤是什么吗?配方的关键是什么吗?
2.解方程3x2-2x-1=0.
提出问题:
(1)如果一个一元二次方程的二次项系数不为1,还能用配方法来解吗?
(2)请将方程3x2-2x-1=0的二次项系数化为1,并尝试解此方程;
(3)由此请你再归纳一下用配方法解一元二次方程的一般步骤.
活动3 知识归纳
1.通过配成________形式来解一元二次方程的方法,叫做配方法.
2.对于任意一元二次方程,用配方法解的一般步骤:①先化成________;②将常数项移到等式右边;③两边除以__________;④方程两边都加上____________
________;⑤将等式左边化成_____________;⑥两边开方,并求出方程的解.
完全平方
一般形式
二次项系数
一次项系数一
半的平方
完全平方形式
提出问题:
(1)配方过程中,在等式两边加上的常数与一次项系数的关系如何?
(2)配方过程中,若等号右边为负数,这个方程有没有实数根?
(3)配方过程中还需注意哪些问题?
活动4 例题与练习
例1.解下列方程:
(1)x2-8x+1=0;(2)2x2+1=3x; (3)3x2-6x+4=0
分析:(1)方程的二次项系数为1,直接运用配方法.
(2)先把方程化成2x2-3x+1=0.它的二次项系数为2,为了便于配方,需将二次项系数化为1,为此方程的两边都除以2.
(3)与(2)类似,方程的两边都除以3后再配方.
解:(1)移项,得
x2-8x=-1,
配方,得
x2-8x+42=-1+42 ,
( x-4)2=15
由此可得
即
配方,得
由此可得
二次项系数化为1,得
解:移项,得
2x2-3x=-1,
即
配方,得
解:移项,得
二次项系数化为1,得
即
因为实数的平方不会是负数,所以x取任何实数时,(x-1)?都是非负数,上式都不成立,即原方程无实数根。
例2 求证:无论x为何值,代数式2x2-4x+3的值恒大于0.
证明:2x2-4x+3
=
=
= 2(x-1)2+1.
∵(x-1)2≥0,∴2(x-1)2+1>0,
∴无论x为何值,代数式2x2-4x+3的值恒大于0.
提出问题:
二次三项式的配方与一元二次方程的配方有什么区别,请指出具体区别在什么地方?
二次三项式配方时,不能除以二次项的系数,只能提取二次项的系数,并添上括号,再用配方法构造一个完全平方式;而一元二次方程配方时,两边除以二次项系数后,再用配方法构造一个完全平方式.
练 习
1.教材P9 练习第1,2题.
2.代数式x2-8x+18的值( )
A.恒为正 B.恒为负
C.可能为0 D.不能确定
3.把方程2x2+6x-1=0配方后得(x+m)2=k,则m=____,k=____.
A
4.式子-x2-4x-5,可配方为-(x+____)2____,该式有最____值,是____.
5.试证明:无论a为何实数,关于x的方程(a2-8a+17)x2+2ax+1=0都是一元二次方程.
证明:∵a2-8a+17=(a-4)2+1>0,
∴无论a为何实数,该方程都是一元二次方程.
2
-1
大
-1
同课章节目录
