22.3 第1课时 二次函数与图形面积问题课件 21PPT
文档属性
| 名称 | 22.3 第1课时 二次函数与图形面积问题课件 21PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 673.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 1970-01-01 08:00:00 | ||
图片预览








文档简介
(共20张PPT)
22.3 实际问题与二次函数
第1课时 二次函数与图形面积问题
一、教学目标
1.让学生能够用二次函数知识解决最值问题(本节主要是面积问题).
2.让学生能够根据实际问题构建二次函数模型.
重点
难点
二、教学重难点
掌握用二次函数求最值来解决图形面积问题.
将实际问题转化为数学问题是本节的难点.
活动1 新课导入
三、教学设计
某公司在甲、乙两座仓库分别有农用车12辆和6辆.现在需要调往A县10辆,需要调往B县8辆,已知从甲仓库调运一辆农用车到A县和B县的运费分别为40元和80元;从乙仓库调运一辆农用车到A县和B县的运费分别为30元和50元.
(1)设乙仓库调往A县农用车x辆,求总运费y关于x的函数关系式;
(2)求最低总运费是多少元?
解:(1)设乙仓库调往A县农用车x辆,则乙仓库调往B县农用车(6-x)辆,甲仓库调往A县农用车(10-x)辆,调往B县农用车(2+x)辆.
根据题意,得y=30x+50(6-x)+40(10-x)+80(2+x)=20x+860(0≤x≤6);
(2)∵k=20>0,
∴y随x的增大而增大,
∴当x=0时,y最小值=860.
∴最低总运费是860元.
活动2 探究新知
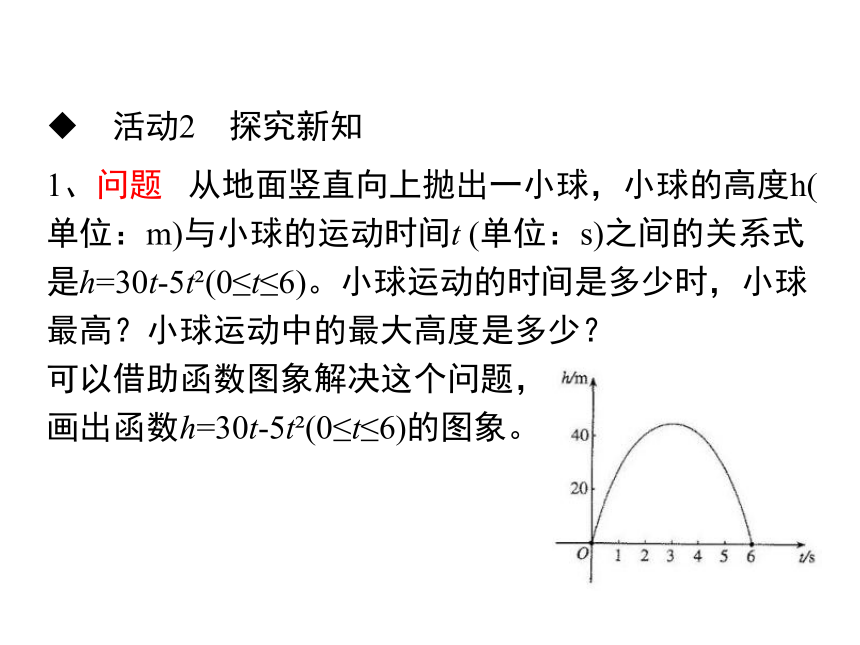
1、问题 从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t (单位:s)之间的关系式是h=30t-5t (0≤t≤6)。小球运动的时间是多少时,小球最高?小球运动中的最大高度是多少?
可以借助函数图象解决这个问题,
画出函数h=30t-5t (0≤t≤6)的图象。
可以看出,这个函数的图象是一条抛物线的一部分,这条抛物线的顶点是这个函数的图象的最高点,也就是说,当t取顶点的横坐标时,这个函数有最大值。
因此,当 时,h有最大值
。也就是说,小球运动的时
间是3s时,小球最高。小球运动的最大高度是45m。
提出问题:
(1)请将二次函数h=30t-5t2(0≤t≤6)化成顶点式,并指出其对称轴和顶点坐标;
(2)请解释该顶点横、纵坐标的含义?
2、探究1
用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长l的变化而变化。当l是多少米时,场地的面积S最大?
分析:
先写出S关于l的函数解析式,再求出使S最大的l值。
解:矩形场地的周长是60m,一边长为l m,所以另一
边长为 m,场地面积S= l (30- l )
即 S= - l +30 l (0<l<30)
因此,当 时,S有最大值
也就是说,当 l 时15m时,场地的面积S最大。
提出问题:
(1)矩形的面积公式是什么?
(2)如何用l表示另一边?面积S关于l的函数解析式是什么?
(3)由函数解析式S=-l2+30 l (0< l <30)可知抛物线的开口方向如何?所以面积S在何时取得最大值?
活动3 知识归纳
一般地,当a>0(a<0)时,抛物线y=ax2+bx+c
的顶点是最______点,也就是说,当x=_____时
,二次函数y=ax2+bx+c有最小(大)值_________.
低(高)
活动4 例题与练习
例1 某广告公司设计一幅周长为12 m的矩形广告牌,广告设计费为每平方米1 000元,设矩形的一边长为x m,面积为S m2.
(1)写出S与x之间的关系式,并写出自变量x的取值范围;
(2)请你设计一个方案,使获得的设计费最多,并求出这个费用.
解:(1)∵矩形的一边长为x m,
∴另一边长为(6-x)m,
∴S=x(6-x)=-x2+6x,其中0<x<6;
(2)∵S=x(6-x)=-x2+6x=-(x-3)2+9,
∴当x=3,即矩形的一边长为3 m时,矩形面积最大,为9 m2,这时设计费最多,为9×1 000=9 000(元).
例2 如图,有长为30 m的篱笆,一面利用墙(墙的最大可用长度为10 m),围成中间隔有一道篱笆(平行于AB)的矩形花圃,设花圃的一边AB为x m,面积为y m2.
(1)求y与x的函数解析式;
(2)y是否有最大值?如果有,请求出y的最大值.
练 习
1.教材P51~5 2 习题22.3第1,3,4题.
2.用长12 m的铝合金条制成使窗户的透光面积最大的矩形窗框(如图),那么这个窗户的最大透光面积是
( )
A.9 m2 B.2 m2 C.6 m2 D.8 m2
C
活动5
完成《名师测控》随堂反馈手册
《精英新课堂》变式训练
活动6 课堂小结
利用二次函数解决几何图形中的最值问题.
四、作业布置与教学反思
1.作业布置
(1)教材P52 习题22.3第5,6,7题;
(2)《名师测控》《精英新课堂》对应课时练习.
2.教学反思
22.3 实际问题与二次函数
第1课时 二次函数与图形面积问题
一、教学目标
1.让学生能够用二次函数知识解决最值问题(本节主要是面积问题).
2.让学生能够根据实际问题构建二次函数模型.
重点
难点
二、教学重难点
掌握用二次函数求最值来解决图形面积问题.
将实际问题转化为数学问题是本节的难点.
活动1 新课导入
三、教学设计
某公司在甲、乙两座仓库分别有农用车12辆和6辆.现在需要调往A县10辆,需要调往B县8辆,已知从甲仓库调运一辆农用车到A县和B县的运费分别为40元和80元;从乙仓库调运一辆农用车到A县和B县的运费分别为30元和50元.
(1)设乙仓库调往A县农用车x辆,求总运费y关于x的函数关系式;
(2)求最低总运费是多少元?
解:(1)设乙仓库调往A县农用车x辆,则乙仓库调往B县农用车(6-x)辆,甲仓库调往A县农用车(10-x)辆,调往B县农用车(2+x)辆.
根据题意,得y=30x+50(6-x)+40(10-x)+80(2+x)=20x+860(0≤x≤6);
(2)∵k=20>0,
∴y随x的增大而增大,
∴当x=0时,y最小值=860.
∴最低总运费是860元.
活动2 探究新知
1、问题 从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t (单位:s)之间的关系式是h=30t-5t (0≤t≤6)。小球运动的时间是多少时,小球最高?小球运动中的最大高度是多少?
可以借助函数图象解决这个问题,
画出函数h=30t-5t (0≤t≤6)的图象。
可以看出,这个函数的图象是一条抛物线的一部分,这条抛物线的顶点是这个函数的图象的最高点,也就是说,当t取顶点的横坐标时,这个函数有最大值。
因此,当 时,h有最大值
。也就是说,小球运动的时
间是3s时,小球最高。小球运动的最大高度是45m。
提出问题:
(1)请将二次函数h=30t-5t2(0≤t≤6)化成顶点式,并指出其对称轴和顶点坐标;
(2)请解释该顶点横、纵坐标的含义?
2、探究1
用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长l的变化而变化。当l是多少米时,场地的面积S最大?
分析:
先写出S关于l的函数解析式,再求出使S最大的l值。
解:矩形场地的周长是60m,一边长为l m,所以另一
边长为 m,场地面积S= l (30- l )
即 S= - l +30 l (0<l<30)
因此,当 时,S有最大值
也就是说,当 l 时15m时,场地的面积S最大。
提出问题:
(1)矩形的面积公式是什么?
(2)如何用l表示另一边?面积S关于l的函数解析式是什么?
(3)由函数解析式S=-l2+30 l (0< l <30)可知抛物线的开口方向如何?所以面积S在何时取得最大值?
活动3 知识归纳
一般地,当a>0(a<0)时,抛物线y=ax2+bx+c
的顶点是最______点,也就是说,当x=_____时
,二次函数y=ax2+bx+c有最小(大)值_________.
低(高)
活动4 例题与练习
例1 某广告公司设计一幅周长为12 m的矩形广告牌,广告设计费为每平方米1 000元,设矩形的一边长为x m,面积为S m2.
(1)写出S与x之间的关系式,并写出自变量x的取值范围;
(2)请你设计一个方案,使获得的设计费最多,并求出这个费用.
解:(1)∵矩形的一边长为x m,
∴另一边长为(6-x)m,
∴S=x(6-x)=-x2+6x,其中0<x<6;
(2)∵S=x(6-x)=-x2+6x=-(x-3)2+9,
∴当x=3,即矩形的一边长为3 m时,矩形面积最大,为9 m2,这时设计费最多,为9×1 000=9 000(元).
例2 如图,有长为30 m的篱笆,一面利用墙(墙的最大可用长度为10 m),围成中间隔有一道篱笆(平行于AB)的矩形花圃,设花圃的一边AB为x m,面积为y m2.
(1)求y与x的函数解析式;
(2)y是否有最大值?如果有,请求出y的最大值.
练 习
1.教材P51~5 2 习题22.3第1,3,4题.
2.用长12 m的铝合金条制成使窗户的透光面积最大的矩形窗框(如图),那么这个窗户的最大透光面积是
( )
A.9 m2 B.2 m2 C.6 m2 D.8 m2
C
活动5
完成《名师测控》随堂反馈手册
《精英新课堂》变式训练
活动6 课堂小结
利用二次函数解决几何图形中的最值问题.
四、作业布置与教学反思
1.作业布置
(1)教材P52 习题22.3第5,6,7题;
(2)《名师测控》《精英新课堂》对应课时练习.
2.教学反思
同课章节目录
