人教版数学九年级上册23.2.1 中心对称课件(16张)
文档属性
| 名称 | 人教版数学九年级上册23.2.1 中心对称课件(16张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 407.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-02 00:00:00 | ||
图片预览





文档简介
23.2 中心对称
?
23.2.1 中心对称
一、教学目标
1.认识两个图形关于某一点中心对称的本质.
2.理解中心对称的性质,并可以判断两个图形是否成中心对称.
3.会画某图形关于某点对称的图形,会确定对称中心.
重点
难点
二、教学重难点
判断两个图形是否成中心对称.
画某图形关于某点对称的图形,确定对称中心.
活动1 新课导入
三、教学设计
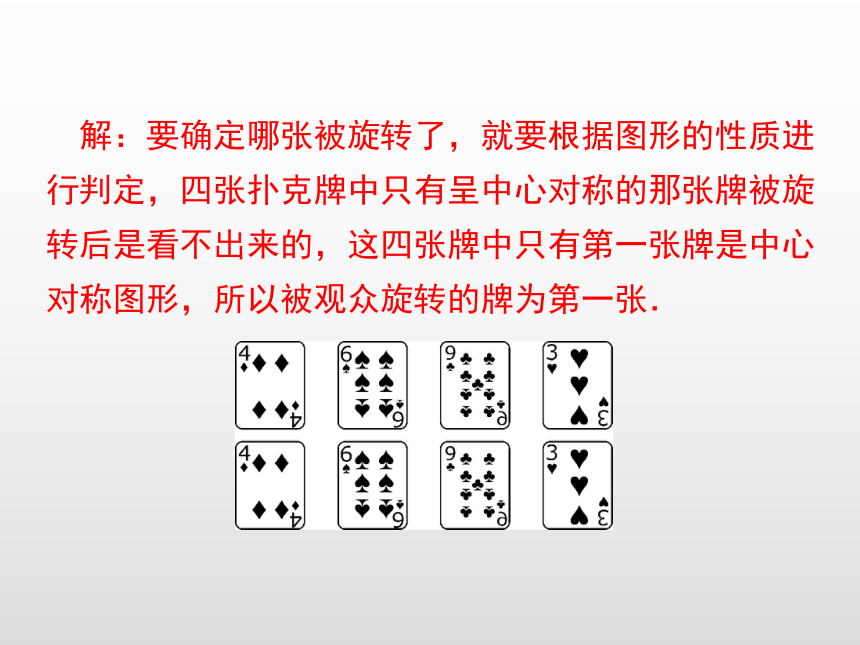
大家都知道,魔术表演很精彩.相信很多同学都看到过这样一个魔术:魔术师把三张扑克牌放在桌子上,如下图(上)所示,然后蒙住眼睛,请一个观众上台,把其中的一张旋转180°放好,魔术师解开蒙着眼睛的布后,看到四张牌如下图(下)所示,他很快确定了被旋转的那一张.聪明的同学们,你知道哪一张被观众旋转过吗?
解:要确定哪张被旋转了,就要根据图形的性质进行判定,四张扑克牌中只有呈中心对称的那张牌被旋转后是看不出来的,这四张牌中只有第一张牌是中心对称图形,所以被观众旋转的牌为第一张.
活动2 探究新知
1、思考
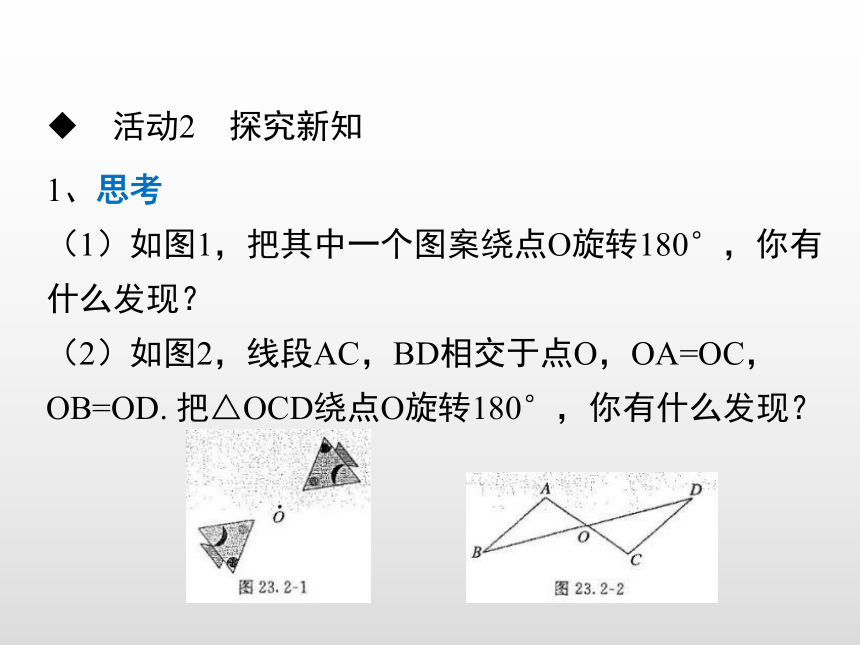
(1)如图1,把其中一个图案绕点O旋转180°,你有什么发现?
(2)如图2,线段AC,BD相交于点O,OA=OC,OB=OD. 把△OCD绕点O旋转180°,你有什么发现?
可以发现,图1中的一个图案旋转后两个图案互相重合;图2中,旋转后△OCD也与△OAB重合。像这样,把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心(简称中心)。这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点。例如,图2中△OCD和△OAB关于点O对称,点C与点A是关于点O的对称点。
2.教材P64~65.
提出问题:
(1)图23.2-3中,△ABC与△A′B′C′全等吗?为什么?
(2)分别连接对应点AA′,BB′,CC′,点O在线段AA′上吗?如果在,在什么位置?
(3)由此你能得到中心对称的性质吗?
活动3 知识归纳
1.把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点____或________;这个点叫做________ (简称中心);这两个图形在旋转后能重合的对应点叫做关于对称中心的______.
2.中心对称的性质:
(1)中心对称的两个图形,对称点所连线段都经过________,而且被对称中心所____;
(2)中心对称的两个图形是____图形.
全等
对称
中心对称
对称中心
对称点
对称中心
平分
活动4 例题与练习
例1 如图,△A′B′C′与△ABC关于点O成中心对称,找出图中的对称点、对称线段.
解:对称点:A与A′,B与B′,C与C′;
对称线段:AB与A′B′,BC与B′C′,AC与A′C′.
例2 如图所示的四组图形中,左边图形与右边图形成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
C
例3 在等腰三角形ABC中,∠ACB=90°,BC=20 cm,如果以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在B′处,求点B′与点B的距离.
解:连接BB′,由中心对称可知,BB′必过点O.
∵△ABC为等腰三角形,
∴AC=BC=20 cm.
∴CO= AC=10 cm.
∴在Rt△BCO中,
∴BB′=2OB=2×10 =20 (cm).
答:点B′与点B的距离为20 cm.
练 习
1.教材P66 练习第1,2题.
2.如图,△ABC与△A′B′C′是成中心对称的两个图形,则下列说法不正确的是( )
A.AO=A′O,BC=B′C′
B.AC∥A′C′
C.∠BAC=∠B′A′C′
D.△ABC≌△A′OC′
D
3.如图,已知△ABC和点O,画出△A′B′C′,使它与△ABC关于点O成中心对称.
解:如图,△A′B′C′就是所求的三角形.
4.如图所示的两个三角形是否成中心对称?若是,请画出对称中心.
解:如图,点O是其对称中心.
?
23.2.1 中心对称
一、教学目标
1.认识两个图形关于某一点中心对称的本质.
2.理解中心对称的性质,并可以判断两个图形是否成中心对称.
3.会画某图形关于某点对称的图形,会确定对称中心.
重点
难点
二、教学重难点
判断两个图形是否成中心对称.
画某图形关于某点对称的图形,确定对称中心.
活动1 新课导入
三、教学设计
大家都知道,魔术表演很精彩.相信很多同学都看到过这样一个魔术:魔术师把三张扑克牌放在桌子上,如下图(上)所示,然后蒙住眼睛,请一个观众上台,把其中的一张旋转180°放好,魔术师解开蒙着眼睛的布后,看到四张牌如下图(下)所示,他很快确定了被旋转的那一张.聪明的同学们,你知道哪一张被观众旋转过吗?
解:要确定哪张被旋转了,就要根据图形的性质进行判定,四张扑克牌中只有呈中心对称的那张牌被旋转后是看不出来的,这四张牌中只有第一张牌是中心对称图形,所以被观众旋转的牌为第一张.
活动2 探究新知
1、思考
(1)如图1,把其中一个图案绕点O旋转180°,你有什么发现?
(2)如图2,线段AC,BD相交于点O,OA=OC,OB=OD. 把△OCD绕点O旋转180°,你有什么发现?
可以发现,图1中的一个图案旋转后两个图案互相重合;图2中,旋转后△OCD也与△OAB重合。像这样,把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心(简称中心)。这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点。例如,图2中△OCD和△OAB关于点O对称,点C与点A是关于点O的对称点。
2.教材P64~65.
提出问题:
(1)图23.2-3中,△ABC与△A′B′C′全等吗?为什么?
(2)分别连接对应点AA′,BB′,CC′,点O在线段AA′上吗?如果在,在什么位置?
(3)由此你能得到中心对称的性质吗?
活动3 知识归纳
1.把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点____或________;这个点叫做________ (简称中心);这两个图形在旋转后能重合的对应点叫做关于对称中心的______.
2.中心对称的性质:
(1)中心对称的两个图形,对称点所连线段都经过________,而且被对称中心所____;
(2)中心对称的两个图形是____图形.
全等
对称
中心对称
对称中心
对称点
对称中心
平分
活动4 例题与练习
例1 如图,△A′B′C′与△ABC关于点O成中心对称,找出图中的对称点、对称线段.
解:对称点:A与A′,B与B′,C与C′;
对称线段:AB与A′B′,BC与B′C′,AC与A′C′.
例2 如图所示的四组图形中,左边图形与右边图形成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
C
例3 在等腰三角形ABC中,∠ACB=90°,BC=20 cm,如果以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在B′处,求点B′与点B的距离.
解:连接BB′,由中心对称可知,BB′必过点O.
∵△ABC为等腰三角形,
∴AC=BC=20 cm.
∴CO= AC=10 cm.
∴在Rt△BCO中,
∴BB′=2OB=2×10 =20 (cm).
答:点B′与点B的距离为20 cm.
练 习
1.教材P66 练习第1,2题.
2.如图,△ABC与△A′B′C′是成中心对称的两个图形,则下列说法不正确的是( )
A.AO=A′O,BC=B′C′
B.AC∥A′C′
C.∠BAC=∠B′A′C′
D.△ABC≌△A′OC′
D
3.如图,已知△ABC和点O,画出△A′B′C′,使它与△ABC关于点O成中心对称.
解:如图,△A′B′C′就是所求的三角形.
4.如图所示的两个三角形是否成中心对称?若是,请画出对称中心.
解:如图,点O是其对称中心.
同课章节目录
