24.1.4第1课时 圆周角定理及其推论课件15 PPT
文档属性
| 名称 | 24.1.4第1课时 圆周角定理及其推论课件15 PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 446.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 1970-01-01 08:00:00 | ||
图片预览






文档简介
24.1.4 圆周角
第1课时 圆周角定理及其推论
一、教学目标
1.学习圆周角、圆周角定理及推论.
2.掌握圆周角与圆心角、直径的关系,能用分类讨论的思想证明圆周角定理.
3.理解圆周角定理的推论,并运用推论进行有关的计算和证明.
重点
难点
二、教学重难点
理解圆周角定理的推论,并运用推论进行有关的计算和证明.
1.运用分类讨论的数学思想证明圆周角定理.
2.独自探索并证明圆周角定理的推论并能应用该推论解决问题.
活动1 新课导入
三、教学设计
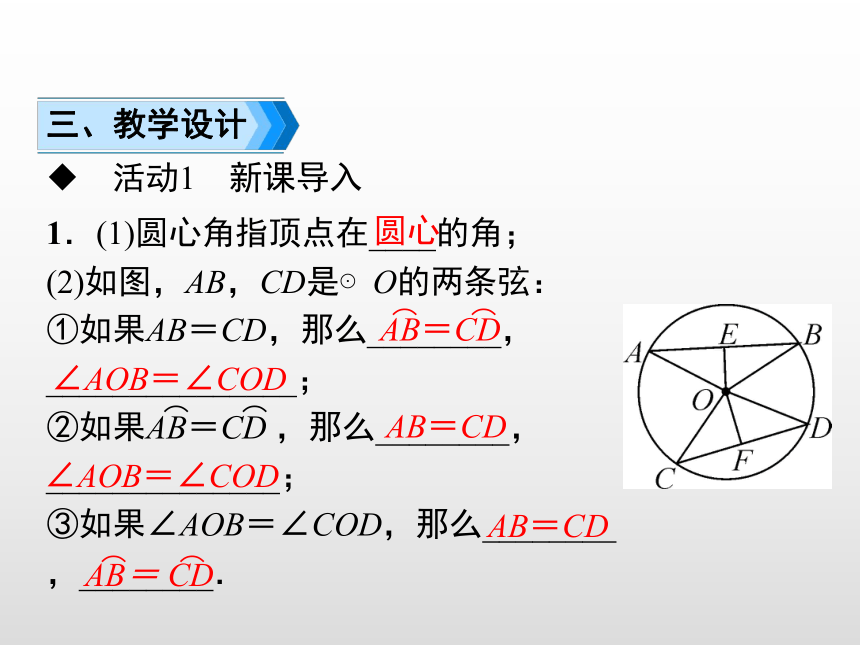
1.(1)圆心角指顶点在____的角;
(2)如图,AB,CD是⊙O的两条弦:
①如果AB=CD,那么________,_______________;
②如果AB=CD ,那么________,______________;
③如果∠AOB=∠COD,那么________,________.
AB= CD
圆心
AB=CD
∠AOB=∠COD
AB=CD
∠AOB=∠COD
AB=CD
(
(
(
(
(
(
活动2 探究新知
1.将圆心角的顶点进行移动,如图①.
(1)当角的顶点在圆心时,我们知道这样的角叫圆心角,如∠AOB.当角的顶点运动到圆周时,如∠ACB. ∠ACB有什么特点?它与∠AOB有何异同?
图①
(2)观察图②,你能仿照圆心角的定义给这类角取一个名字并下个定义吗?
(3)比较概念:圆心角定义中为什么没有提到“两边都与圆相交”呢?
图②
2、探究
分别测量图11中AB所对的圆周角∠ACB和圆心角∠AOB的度数,它们之间有什么关系?
在⊙O上任取一条弧,作出这条弧所对的圆周角和圆心角,测量它们的度数,你能得出同样的结论吗?由此你能发现什么规律?
(
可以发现,同弧所对的圆周角的度数等于这个这条弧所对的圆心角的度数的一半。
提出问题:
(1)经过测量,图24.1-11中的圆周角∠ACB和圆心角∠AOB之间有什么关系?
(2)任意作一个圆,任取一条弧,作出它所对的圆周角与圆心角,测量它们的度数,你发现什么规律?
(3)一条弧所对的圆心角有几个?所对的圆周角有几个?
(4)改变动点C在圆周上的位置,看看圆周角的度数有没有变化?你发现了什么?
(5)如果把上述发现的结论中的“同弧”改为“等弧”,结论还正确吗?
(6)如图③,BC是⊙O的直径.请问:BC所对的圆周角∠BAC是锐角、直角还是钝角?
(7)如图④,若圆周角∠BAC=90°,那么它所对的弦BC经过圆心吗?为什么?由此能得出什么结论?
图③
图④
活动3 知识归纳
1.顶点在____, 并且两边都与圆____的角叫做圆周角.
2.在同圆或等圆中,____或____所对的圆周角相等,都等于这条弧所对的______的一半.
3.在同圆或等圆中,相等的圆周角所对的弧也____.
4.半圆(或直径)所对的圆周角是____,90°的圆周角所对的弦是____.
圆上
相交
等弧
等弦
圆心角
相等
直角
直径
活动4 例题与练习
例1 如图14, ⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于点D,求BC,AD,BD的长.
解:如图15,连接OD.
∵AB是直径,
∴∠ACB=∠ADB=90°
在Rt△ABC中,
∵CD平分∠ACB,∴ ∠ACD= ∠BCD,
∴ ∠AOD= ∠BOD. ∴ AD =BD.
又 在Rt△ABD中,
AD ?+BD?=AB?
∴AD=BD= AB= ×10=
例2 如图,△ABC的顶点都在⊙O上,AD是⊙O的直径,AD= ,∠B=∠DAC,则AC=____.
1
例3 如图,AB是⊙O的直径,AB=10 cm,∠ADE=60°,DC平分∠ADE,求AC,BC的长.
解:∵∠ADE=60°,DC平分∠ADE,
∴∠ADC= ∠ADE=30°,
∴∠ABC=∠ADC=30°.
又∵AB为⊙O的直径,
∴∠ACB=90°,
∴AC= AB=5 cm.
∴
练 习
1.教材P88 练习第1,3,4题.
2.如图,已知圆心角∠BOC=100°,点A为优弧上一点,则圆周角∠BAC的度数为_____.
3.如图,OA为⊙O的半径,以OA为直径的⊙C与⊙O的弦AB相交于点D.若OD=5 cm,则BE=_____.
(第3题图)
50°
10cm
(第2题图)
第1课时 圆周角定理及其推论
一、教学目标
1.学习圆周角、圆周角定理及推论.
2.掌握圆周角与圆心角、直径的关系,能用分类讨论的思想证明圆周角定理.
3.理解圆周角定理的推论,并运用推论进行有关的计算和证明.
重点
难点
二、教学重难点
理解圆周角定理的推论,并运用推论进行有关的计算和证明.
1.运用分类讨论的数学思想证明圆周角定理.
2.独自探索并证明圆周角定理的推论并能应用该推论解决问题.
活动1 新课导入
三、教学设计
1.(1)圆心角指顶点在____的角;
(2)如图,AB,CD是⊙O的两条弦:
①如果AB=CD,那么________,_______________;
②如果AB=CD ,那么________,______________;
③如果∠AOB=∠COD,那么________,________.
AB= CD
圆心
AB=CD
∠AOB=∠COD
AB=CD
∠AOB=∠COD
AB=CD
(
(
(
(
(
(
活动2 探究新知
1.将圆心角的顶点进行移动,如图①.
(1)当角的顶点在圆心时,我们知道这样的角叫圆心角,如∠AOB.当角的顶点运动到圆周时,如∠ACB. ∠ACB有什么特点?它与∠AOB有何异同?
图①
(2)观察图②,你能仿照圆心角的定义给这类角取一个名字并下个定义吗?
(3)比较概念:圆心角定义中为什么没有提到“两边都与圆相交”呢?
图②
2、探究
分别测量图11中AB所对的圆周角∠ACB和圆心角∠AOB的度数,它们之间有什么关系?
在⊙O上任取一条弧,作出这条弧所对的圆周角和圆心角,测量它们的度数,你能得出同样的结论吗?由此你能发现什么规律?
(
可以发现,同弧所对的圆周角的度数等于这个这条弧所对的圆心角的度数的一半。
提出问题:
(1)经过测量,图24.1-11中的圆周角∠ACB和圆心角∠AOB之间有什么关系?
(2)任意作一个圆,任取一条弧,作出它所对的圆周角与圆心角,测量它们的度数,你发现什么规律?
(3)一条弧所对的圆心角有几个?所对的圆周角有几个?
(4)改变动点C在圆周上的位置,看看圆周角的度数有没有变化?你发现了什么?
(5)如果把上述发现的结论中的“同弧”改为“等弧”,结论还正确吗?
(6)如图③,BC是⊙O的直径.请问:BC所对的圆周角∠BAC是锐角、直角还是钝角?
(7)如图④,若圆周角∠BAC=90°,那么它所对的弦BC经过圆心吗?为什么?由此能得出什么结论?
图③
图④
活动3 知识归纳
1.顶点在____, 并且两边都与圆____的角叫做圆周角.
2.在同圆或等圆中,____或____所对的圆周角相等,都等于这条弧所对的______的一半.
3.在同圆或等圆中,相等的圆周角所对的弧也____.
4.半圆(或直径)所对的圆周角是____,90°的圆周角所对的弦是____.
圆上
相交
等弧
等弦
圆心角
相等
直角
直径
活动4 例题与练习
例1 如图14, ⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于点D,求BC,AD,BD的长.
解:如图15,连接OD.
∵AB是直径,
∴∠ACB=∠ADB=90°
在Rt△ABC中,
∵CD平分∠ACB,∴ ∠ACD= ∠BCD,
∴ ∠AOD= ∠BOD. ∴ AD =BD.
又 在Rt△ABD中,
AD ?+BD?=AB?
∴AD=BD= AB= ×10=
例2 如图,△ABC的顶点都在⊙O上,AD是⊙O的直径,AD= ,∠B=∠DAC,则AC=____.
1
例3 如图,AB是⊙O的直径,AB=10 cm,∠ADE=60°,DC平分∠ADE,求AC,BC的长.
解:∵∠ADE=60°,DC平分∠ADE,
∴∠ADC= ∠ADE=30°,
∴∠ABC=∠ADC=30°.
又∵AB为⊙O的直径,
∴∠ACB=90°,
∴AC= AB=5 cm.
∴
练 习
1.教材P88 练习第1,3,4题.
2.如图,已知圆心角∠BOC=100°,点A为优弧上一点,则圆周角∠BAC的度数为_____.
3.如图,OA为⊙O的半径,以OA为直径的⊙C与⊙O的弦AB相交于点D.若OD=5 cm,则BE=_____.
(第3题图)
50°
10cm
(第2题图)
同课章节目录
