24.1.4第2课时 圆内接四边形课件12 PPT
文档属性
| 名称 | 24.1.4第2课时 圆内接四边形课件12 PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 267.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 1970-01-01 08:00:00 | ||
图片预览





文档简介
第2课时 圆内接四边形
一、教学目标
1.掌握圆内接多边形、多边形的外接圆的概念.
2.理解圆内接四边形的性质.
3.通过探究讨论,培养学生的推理能力.
重点
难点
二、教学重难点
圆内接四边形性质的探究及运用.
圆内接四边形性质的灵活运用以及几何图形中辅助线的添加.
活动1 新课导入
三、教学设计
1.圆周角定理及其推论.
2.如图,点A,B,C在⊙O上,连接OA,OB.若∠ABO=25°,则∠C=____.
3.如图,点A,B,C在⊙O上,已知∠B=60°,则∠CAO=____.
(第2题图)
65°
30°
(第3题图)
活动2 探究新知
1、思考
圆内接四边形的4个角之间有什么关系?
因为圆内接四边形的每一个角都是圆周角,所以我们可以利用圆周角定理,来研究圆内接四边形的角之间的关系
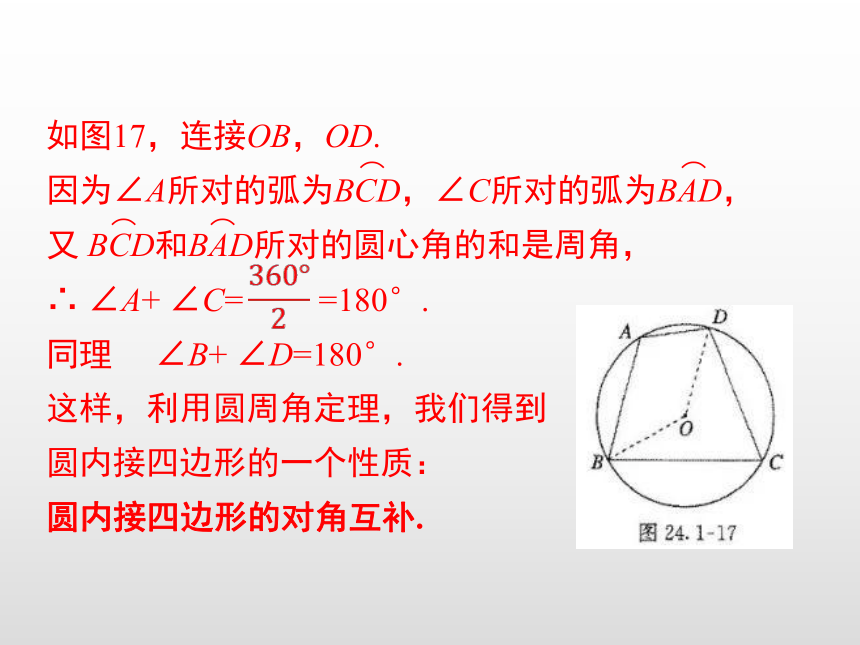
如图17,连接OB,OD.
因为∠A所对的弧为BCD,∠C所对的弧为BAD,
又 BCD和BAD所对的圆心角的和是周角,
∴ ∠A+ ∠C= =180°.
同理 ∠B+ ∠D=180°.
这样,利用圆周角定理,我们得到
圆内接四边形的一个性质:
圆内接四边形的对角互补.
(
(
(
(
提出问题:
(1) 图24.1-17中,∠A是圆周角吗?∠ABC,∠C,∠ADC呢?
(2) ∠A与∠C,∠ABC与∠ADC之间有什么关系?用圆周角定理尝试证明;
(3) 由此你能得出圆内接四边形的什么结论?
活动3 知识归纳
1.如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做_____________,这个圆叫做这个多边形的_______.
2.圆内接四边形的对角____.
互补
圆内接多边形
外接圆
活动4 例题与练习
例1 在圆内接四边形ABCD中,∠A,∠B,∠C的度数的比是3∶2∶7,求四边形各内角的度数.
解:设∠A,∠B,∠C的度数分别为3x,2x,7x.
∵四边形ABCD是圆内接四边形,
∴∠A+∠C=180°,即 3x+7x=180°,
∴x=18°,
∴∠A=3x=54°,∠B=2x=36°,∠C=7x=126°.
又∵∠B+∠D=180°,
∴∠D=180°-36°=144°.
例2 如图,已知A,B,C,D四点共圆,且AC=BC.
求证:DC平分∠BDE.
解:∵A,B,C,D四点共圆,
∴∠CDA+∠ABC=180°,
又∵∠3+∠CDA=180°,
∴∠3=∠ABC. 又∵AC=BC,
∴∠1=∠ABC,∴∠1=∠3.
又∵∠1=∠2,∴∠2=∠3,
即 DC平分∠BDE.
练 习
1.教材P88 练习第2,5题.
2.如图,四边形ABCD内接于⊙O,四边形ABCO是平行四边形,则∠ADC等于( )
A.45° B.50° C.60° D.75°
3.如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠BOD的度数为_____.
(第2题图)
(第3题图)
128°
C
4.如图,在⊙O中,∠CBD=30°,∠BDC=20°,求∠A的度数.
解:∵在△BCD中,∠CBD=30°,∠BDC=20°,
∴∠C=180°-∠CBD-∠BDC=130°.
∵四边形ABCD是圆内接四边形,
∴∠A=180°-∠C=50°.
一、教学目标
1.掌握圆内接多边形、多边形的外接圆的概念.
2.理解圆内接四边形的性质.
3.通过探究讨论,培养学生的推理能力.
重点
难点
二、教学重难点
圆内接四边形性质的探究及运用.
圆内接四边形性质的灵活运用以及几何图形中辅助线的添加.
活动1 新课导入
三、教学设计
1.圆周角定理及其推论.
2.如图,点A,B,C在⊙O上,连接OA,OB.若∠ABO=25°,则∠C=____.
3.如图,点A,B,C在⊙O上,已知∠B=60°,则∠CAO=____.
(第2题图)
65°
30°
(第3题图)
活动2 探究新知
1、思考
圆内接四边形的4个角之间有什么关系?
因为圆内接四边形的每一个角都是圆周角,所以我们可以利用圆周角定理,来研究圆内接四边形的角之间的关系
如图17,连接OB,OD.
因为∠A所对的弧为BCD,∠C所对的弧为BAD,
又 BCD和BAD所对的圆心角的和是周角,
∴ ∠A+ ∠C= =180°.
同理 ∠B+ ∠D=180°.
这样,利用圆周角定理,我们得到
圆内接四边形的一个性质:
圆内接四边形的对角互补.
(
(
(
(
提出问题:
(1) 图24.1-17中,∠A是圆周角吗?∠ABC,∠C,∠ADC呢?
(2) ∠A与∠C,∠ABC与∠ADC之间有什么关系?用圆周角定理尝试证明;
(3) 由此你能得出圆内接四边形的什么结论?
活动3 知识归纳
1.如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做_____________,这个圆叫做这个多边形的_______.
2.圆内接四边形的对角____.
互补
圆内接多边形
外接圆
活动4 例题与练习
例1 在圆内接四边形ABCD中,∠A,∠B,∠C的度数的比是3∶2∶7,求四边形各内角的度数.
解:设∠A,∠B,∠C的度数分别为3x,2x,7x.
∵四边形ABCD是圆内接四边形,
∴∠A+∠C=180°,即 3x+7x=180°,
∴x=18°,
∴∠A=3x=54°,∠B=2x=36°,∠C=7x=126°.
又∵∠B+∠D=180°,
∴∠D=180°-36°=144°.
例2 如图,已知A,B,C,D四点共圆,且AC=BC.
求证:DC平分∠BDE.
解:∵A,B,C,D四点共圆,
∴∠CDA+∠ABC=180°,
又∵∠3+∠CDA=180°,
∴∠3=∠ABC. 又∵AC=BC,
∴∠1=∠ABC,∴∠1=∠3.
又∵∠1=∠2,∴∠2=∠3,
即 DC平分∠BDE.
练 习
1.教材P88 练习第2,5题.
2.如图,四边形ABCD内接于⊙O,四边形ABCO是平行四边形,则∠ADC等于( )
A.45° B.50° C.60° D.75°
3.如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠BOD的度数为_____.
(第2题图)
(第3题图)
128°
C
4.如图,在⊙O中,∠CBD=30°,∠BDC=20°,求∠A的度数.
解:∵在△BCD中,∠CBD=30°,∠BDC=20°,
∴∠C=180°-∠CBD-∠BDC=130°.
∵四边形ABCD是圆内接四边形,
∴∠A=180°-∠C=50°.
同课章节目录
