人教版九年级数学上册23.1 图形的旋转能力提升卷(Word版 含答案)
文档属性
| 名称 | 人教版九年级数学上册23.1 图形的旋转能力提升卷(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 310.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-01 14:46:32 | ||
图片预览



文档简介
人教版九年级数学上册23.1
图形的旋转
能力提升卷
一、选择题(共10小题,3
10=30)
1.下列旋转的旋转中心为点A的是(
)
A
B
C
D
2.如图,△ABC和△ADE均为等边三角形,则图中可以看成是旋转关系的三角形是( )
A.△ABC和△ADE
B.△ABC和△ABD
C.△ABD和△ACE
D.△ACE和△ADE
3.在俄罗斯方块游戏中,已拼好的图案如图,现在出现一小方格正向下运动,则要使其拼成一个完整的图形,使所有图案消失,则必须进行(
)
A.顺时针旋转90°,向右平移
B.逆时针旋转90°,向右平移
C.顺时针旋转90°,向下平移
D.逆时针旋转90°,向下平移
4.如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B,D两点间的距离为(
)
A.
B.2
C.3
D.2
5.如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是(
)
A.55°
B.60°
C.65°
D.70°
6.
如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4,则下列结论错误的是(
)
A.AE∥BC
B.∠ADE=∠BDC
C.△BDE是等边三角形
D.△ADE的周长是9
7.如图,将△OAB绕点O逆时针旋转70°到△OCD的位置,若∠AOB=40°,则∠AOD=( )
A.45°
B.40°
C.35°
D.30°
8.如图,在△ABC中,AB=2,BC=3.6,∠B=60°,将△ABC绕点A顺时针旋转得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为(
)
A.1.6
B.1.8
C.2
D.2.6
9.如图,四边形ABCD是边长为5的正方形,E是DC上一点,DE=1,将△ADE绕着点A顺时针旋转到与△ABF重合,则EF=( )
A.
B.
C.5
D.2
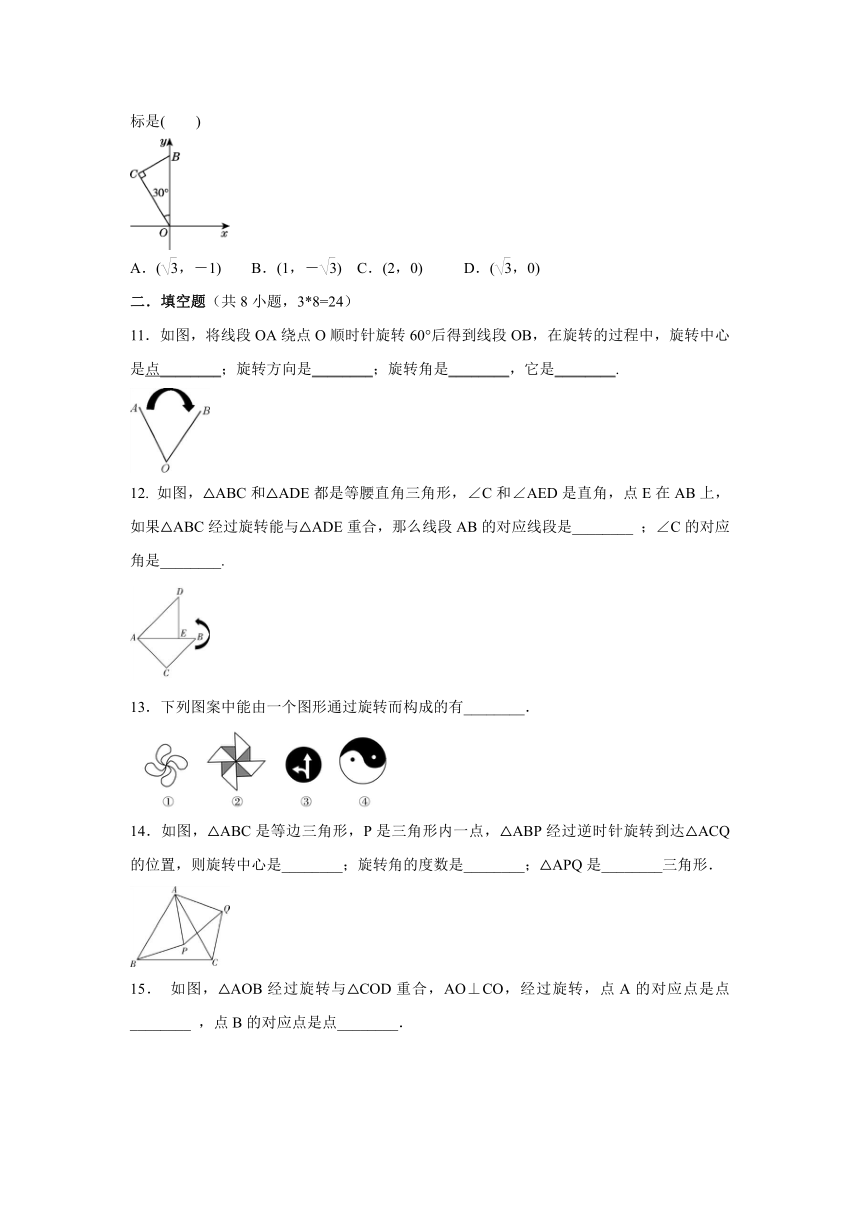
10.如图,Rt△OCB的斜边在y轴上,OC=,含30°角的顶点与原点重合,直角顶点C在第二象限,将Rt△OCB绕原点顺时针旋转120°后得到△OC′B′,则B点的对应点B′的坐标是( )
A.(,-1)
B.(1,-)
C.(2,0)
D.(,0)
二.填空题(共8小题,3
8=24)
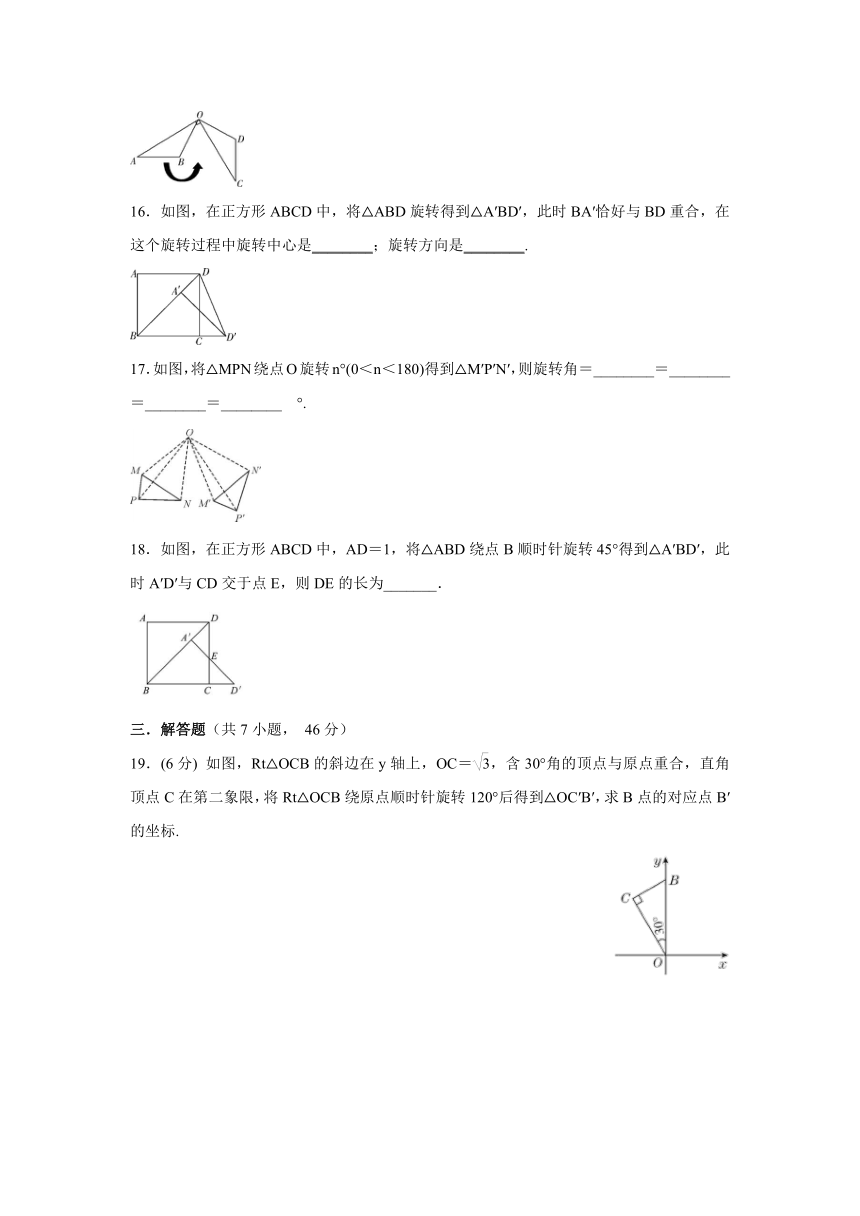
11.如图,将线段OA绕点O顺时针旋转60°后得到线段OB,在旋转的过程中,旋转中心是点________;旋转方向是________;旋转角是________,它是________.
12.
如图,△ABC和△ADE都是等腰直角三角形,∠C和∠AED是直角,点E在AB上,如果△ABC经过旋转能与△ADE重合,那么线段AB的对应线段是________
;∠C的对应角是________.
13.下列图案中能由一个图形通过旋转而构成的有________.
14.如图,△ABC是等边三角形,P是三角形内一点,△ABP经过逆时针旋转到达△ACQ的位置,则旋转中心是________;旋转角的度数是________;△APQ是________三角形.
15.
如图,△AOB经过旋转与△COD重合,AO⊥CO,经过旋转,点A的对应点是点________
,点B的对应点是点________.
16.如图,在正方形ABCD中,将△ABD旋转得到△A′BD′,此时BA′恰好与BD重合,在这个旋转过程中旋转中心是________;旋转方向是________.
17.如图,将△MPN绕点O旋转n°(0<n<180)得到△M′P′N′,则旋转角=________=________=________=________
°.
18.如图,在正方形ABCD中,AD=1,将△ABD绕点B顺时针旋转45°得到△A′BD′,此时A′D′与CD交于点E,则DE的长为_______.
三.解答题(共7小题,
46分)
19.(6分)
如图,Rt△OCB的斜边在y轴上,OC=,含30°角的顶点与原点重合,直角顶点C在第二象限,将Rt△OCB绕原点顺时针旋转120°后得到△OC′B′,求B点的对应点B′的坐标.
20.(6分)
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=25°,求∠BAA′的度数.
21.(6分)
如图,已知AC⊥BC,垂足为C,AC=4,BC=3
,将线段AC绕点A按逆时针方向旋转60°,得到线段AD,连接DC,DB.
求:(1)线段DC的长度;(2)线段DB的长度.
22.(6分)
如图,将矩形ABCD绕点A旋转至矩形AB′C′D′的位置,此时AC′的中点恰好与点D重合,AB′交CD于点E.若AB=3,求△AEC的面积.
23.(6分)
如图,将边长为1的正方形ABCD绕点A逆时针旋转30°得到正方形AB′C′D′,求图中阴影部分的面积.
24.(8分)
如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连接CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连接DE交BC于点F,连接BE.
(1)求证:△ACD≌△BCE;
(2)当AD=BF时,求∠BEF的度数.
25.(8分)
如图,△ABC是等边三角形,点O是△ABC内一点,BO=6,CO=10,AO=8.
(1)将△BOC绕点B逆时针旋转60°,得到△BO′A,画出△BO′A;
(2)求∠AOB的度数;
(3)设S△AOB+S△BOC=m,S△BOC+S△AOC=n,求m,n的值.
参考答案
1-5ACAAC
6-10BDADA
11.
点O;顺时针;∠AOB
,60
12.
AD;∠AED
13.
①②
14.
点A;60°;等边
15.
点C,点D
16.
点B;顺时针
17.
∠MOM′,∠POP′,∠NO
N′,n
18.
2-2
19.
解:如图,旋转后点C′在x轴上,点B′在第四象限,且OC′=OC=,∠B′OC′=∠BOC=30°.
在Rt△B′OC′中,OB′=2B′C′,OC′2+B′C′2=OB′2,
即B′C′2+3=4B′C′2,∴B′C′=1.
∴点B′的坐标为(,-1).
20.
解:∵将Rt△ABC绕直角顶点C顺时针旋转90°得到△A′B′C,
∴AC=A′C,∴△ACA′是等腰直角三角形,
∴∠CA′A=∠CAA′=45°,∴∠CA′B′=20°=∠BAC,
∴∠BAA′=20°+45°=65°.
21.
解:(1)∵AC=AD,∠CAD=60°,
∴△ACD是等边三角形,∴DC=AC=4.
(2)如图,过点D作DE⊥BC于点E.
∵△ACD是等边三角形,
∴∠ACD=60°.
又∵AC⊥BC,
∴∠DCE=∠ACB-∠ACD=90°-60°=30°,
∴在Rt△CDE中,DE=DC=2,CE==2
,
∴BE=BC-CE=3
-2
=,
∴BD===.
22.
解:∵旋转后AC′的中点恰好与点D重合,
即AD=AC′=AC,
∴在Rt△ACD中,∠ACD=30°,∠DAC=60°,
∴∠C′AD′=60°,∴∠DAE=30°,
∴∠EAC=∠ACD=30°,
∴AE=CE,AD=.
设AE=CE=x,则有DE=DC-CE=AB-CE=3-x.
在Rt△ADE中,根据勾股定理,得x2=(3-x)2+()2,
解得x=2,
∴CE=2,则S△AEC=CE·AD=.
23.
解:如图,设B′C′与CD的交点为E,连接AE.在Rt△AB′E和Rt△ADE中,∵AE=AE,AB′=AD,∴Rt△AB′E≌Rt△ADE(HL),
∴∠DAE=∠B′AE.
∵旋转角为30°,∴∠DAB′=60°,
∴∠DAE=×60°=30°,
∴DE=AE,则DE2=4DE2-1,∴DE=,
∴阴影部分的面积=1×1-2×=1-.
24.
解:(1)证明:由线段CD绕点C逆时针旋转90°得到线段CE,得CD=CE,∠DCE=90°.∵∠ACB=90°,∴∠ACD=∠BCE.
在△ACD与△BCE中,
∴△ACD≌△BCE(SAS)
(2)由(1)知△ACD≌△BCE,∴∠A=∠FBE,AD=BE.
∵AC=BC,∠ACB=90°,∴∠A=∠ABC=45°.
∴∠FBE=∠A=45°
∵AD=BF,∴BF=BE.
∴∠BEF=∠BFE==67.5°
25.
解:(1)如图所示
(2)连接OO′,易得△BOO′为等边三角形,∴OO′=6,
在△AO′O中,AO=8,OO′=6,O′A=10,
∴△AOO′=90°,
∴∠AOB=90°+60°=150°
(3)由(2)知,S△AOB+S△BOC=S△AOO′+S△BOO′=×6×8+×62,
即m=24+9,
将△ABO绕点A逆时针旋转60°,得到△ACO1,
同法可求得,n=S△AOO1+S△OCO1,
易得△AOO1为边长为8的等边三角形,
△OCO1中∠OO1C=90°,
故n=×6×8+×82=24+16
图形的旋转
能力提升卷
一、选择题(共10小题,3
10=30)
1.下列旋转的旋转中心为点A的是(
)
A
B
C
D
2.如图,△ABC和△ADE均为等边三角形,则图中可以看成是旋转关系的三角形是( )
A.△ABC和△ADE
B.△ABC和△ABD
C.△ABD和△ACE
D.△ACE和△ADE
3.在俄罗斯方块游戏中,已拼好的图案如图,现在出现一小方格正向下运动,则要使其拼成一个完整的图形,使所有图案消失,则必须进行(
)
A.顺时针旋转90°,向右平移
B.逆时针旋转90°,向右平移
C.顺时针旋转90°,向下平移
D.逆时针旋转90°,向下平移
4.如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B,D两点间的距离为(
)
A.
B.2
C.3
D.2
5.如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是(
)
A.55°
B.60°
C.65°
D.70°
6.
如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4,则下列结论错误的是(
)
A.AE∥BC
B.∠ADE=∠BDC
C.△BDE是等边三角形
D.△ADE的周长是9
7.如图,将△OAB绕点O逆时针旋转70°到△OCD的位置,若∠AOB=40°,则∠AOD=( )
A.45°
B.40°
C.35°
D.30°
8.如图,在△ABC中,AB=2,BC=3.6,∠B=60°,将△ABC绕点A顺时针旋转得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为(
)
A.1.6
B.1.8
C.2
D.2.6
9.如图,四边形ABCD是边长为5的正方形,E是DC上一点,DE=1,将△ADE绕着点A顺时针旋转到与△ABF重合,则EF=( )
A.
B.
C.5
D.2
10.如图,Rt△OCB的斜边在y轴上,OC=,含30°角的顶点与原点重合,直角顶点C在第二象限,将Rt△OCB绕原点顺时针旋转120°后得到△OC′B′,则B点的对应点B′的坐标是( )
A.(,-1)
B.(1,-)
C.(2,0)
D.(,0)
二.填空题(共8小题,3
8=24)
11.如图,将线段OA绕点O顺时针旋转60°后得到线段OB,在旋转的过程中,旋转中心是点________;旋转方向是________;旋转角是________,它是________.
12.
如图,△ABC和△ADE都是等腰直角三角形,∠C和∠AED是直角,点E在AB上,如果△ABC经过旋转能与△ADE重合,那么线段AB的对应线段是________
;∠C的对应角是________.
13.下列图案中能由一个图形通过旋转而构成的有________.
14.如图,△ABC是等边三角形,P是三角形内一点,△ABP经过逆时针旋转到达△ACQ的位置,则旋转中心是________;旋转角的度数是________;△APQ是________三角形.
15.
如图,△AOB经过旋转与△COD重合,AO⊥CO,经过旋转,点A的对应点是点________
,点B的对应点是点________.
16.如图,在正方形ABCD中,将△ABD旋转得到△A′BD′,此时BA′恰好与BD重合,在这个旋转过程中旋转中心是________;旋转方向是________.
17.如图,将△MPN绕点O旋转n°(0<n<180)得到△M′P′N′,则旋转角=________=________=________=________
°.
18.如图,在正方形ABCD中,AD=1,将△ABD绕点B顺时针旋转45°得到△A′BD′,此时A′D′与CD交于点E,则DE的长为_______.
三.解答题(共7小题,
46分)
19.(6分)
如图,Rt△OCB的斜边在y轴上,OC=,含30°角的顶点与原点重合,直角顶点C在第二象限,将Rt△OCB绕原点顺时针旋转120°后得到△OC′B′,求B点的对应点B′的坐标.
20.(6分)
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=25°,求∠BAA′的度数.
21.(6分)
如图,已知AC⊥BC,垂足为C,AC=4,BC=3
,将线段AC绕点A按逆时针方向旋转60°,得到线段AD,连接DC,DB.
求:(1)线段DC的长度;(2)线段DB的长度.
22.(6分)
如图,将矩形ABCD绕点A旋转至矩形AB′C′D′的位置,此时AC′的中点恰好与点D重合,AB′交CD于点E.若AB=3,求△AEC的面积.
23.(6分)
如图,将边长为1的正方形ABCD绕点A逆时针旋转30°得到正方形AB′C′D′,求图中阴影部分的面积.
24.(8分)
如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连接CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连接DE交BC于点F,连接BE.
(1)求证:△ACD≌△BCE;
(2)当AD=BF时,求∠BEF的度数.
25.(8分)
如图,△ABC是等边三角形,点O是△ABC内一点,BO=6,CO=10,AO=8.
(1)将△BOC绕点B逆时针旋转60°,得到△BO′A,画出△BO′A;
(2)求∠AOB的度数;
(3)设S△AOB+S△BOC=m,S△BOC+S△AOC=n,求m,n的值.
参考答案
1-5ACAAC
6-10BDADA
11.
点O;顺时针;∠AOB
,60
12.
AD;∠AED
13.
①②
14.
点A;60°;等边
15.
点C,点D
16.
点B;顺时针
17.
∠MOM′,∠POP′,∠NO
N′,n
18.
2-2
19.
解:如图,旋转后点C′在x轴上,点B′在第四象限,且OC′=OC=,∠B′OC′=∠BOC=30°.
在Rt△B′OC′中,OB′=2B′C′,OC′2+B′C′2=OB′2,
即B′C′2+3=4B′C′2,∴B′C′=1.
∴点B′的坐标为(,-1).
20.
解:∵将Rt△ABC绕直角顶点C顺时针旋转90°得到△A′B′C,
∴AC=A′C,∴△ACA′是等腰直角三角形,
∴∠CA′A=∠CAA′=45°,∴∠CA′B′=20°=∠BAC,
∴∠BAA′=20°+45°=65°.
21.
解:(1)∵AC=AD,∠CAD=60°,
∴△ACD是等边三角形,∴DC=AC=4.
(2)如图,过点D作DE⊥BC于点E.
∵△ACD是等边三角形,
∴∠ACD=60°.
又∵AC⊥BC,
∴∠DCE=∠ACB-∠ACD=90°-60°=30°,
∴在Rt△CDE中,DE=DC=2,CE==2
,
∴BE=BC-CE=3
-2
=,
∴BD===.
22.
解:∵旋转后AC′的中点恰好与点D重合,
即AD=AC′=AC,
∴在Rt△ACD中,∠ACD=30°,∠DAC=60°,
∴∠C′AD′=60°,∴∠DAE=30°,
∴∠EAC=∠ACD=30°,
∴AE=CE,AD=.
设AE=CE=x,则有DE=DC-CE=AB-CE=3-x.
在Rt△ADE中,根据勾股定理,得x2=(3-x)2+()2,
解得x=2,
∴CE=2,则S△AEC=CE·AD=.
23.
解:如图,设B′C′与CD的交点为E,连接AE.在Rt△AB′E和Rt△ADE中,∵AE=AE,AB′=AD,∴Rt△AB′E≌Rt△ADE(HL),
∴∠DAE=∠B′AE.
∵旋转角为30°,∴∠DAB′=60°,
∴∠DAE=×60°=30°,
∴DE=AE,则DE2=4DE2-1,∴DE=,
∴阴影部分的面积=1×1-2×=1-.
24.
解:(1)证明:由线段CD绕点C逆时针旋转90°得到线段CE,得CD=CE,∠DCE=90°.∵∠ACB=90°,∴∠ACD=∠BCE.
在△ACD与△BCE中,
∴△ACD≌△BCE(SAS)
(2)由(1)知△ACD≌△BCE,∴∠A=∠FBE,AD=BE.
∵AC=BC,∠ACB=90°,∴∠A=∠ABC=45°.
∴∠FBE=∠A=45°
∵AD=BF,∴BF=BE.
∴∠BEF=∠BFE==67.5°
25.
解:(1)如图所示
(2)连接OO′,易得△BOO′为等边三角形,∴OO′=6,
在△AO′O中,AO=8,OO′=6,O′A=10,
∴△AOO′=90°,
∴∠AOB=90°+60°=150°
(3)由(2)知,S△AOB+S△BOC=S△AOO′+S△BOO′=×6×8+×62,
即m=24+9,
将△ABO绕点A逆时针旋转60°,得到△ACO1,
同法可求得,n=S△AOO1+S△OCO1,
易得△AOO1为边长为8的等边三角形,
△OCO1中∠OO1C=90°,
故n=×6×8+×82=24+16
同课章节目录
