2020年秋人教版九年级数学上册随堂练22.1.4 二次函数y=ax2 bx c的图象和性质拓展练习(Word版 含答案)
文档属性
| 名称 | 2020年秋人教版九年级数学上册随堂练22.1.4 二次函数y=ax2 bx c的图象和性质拓展练习(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 128.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-01 00:00:00 | ||
图片预览


文档简介
22.1.4
二次函数y=ax2+bx+c的图象和性质拓展练习
一、选择题
1.将抛物线y=2x2﹣1先向左平移1个单位长度,再向上平移2个单位长度,得到的抛物线的顶点坐标为( )
A.(0,﹣1)
B.(1,1)
C.(﹣1,﹣3)
D.(﹣1,1)
2.已知二次函数y=x2﹣6x+1,关于该函数在﹣1≤x≤4的取值范围内,下列说法正确的是( )
A.有最大值8,最小值﹣8
B.有最大值8,最小值﹣7C.有最大值﹣7,最小值﹣8
D.有最大值1,最小值﹣7
3.已知非负数,,满足,,设的最大值为,最小值为,则的值为(
)
A.
B.
C.
D.
4.若二次函数y=x2+bx+4配方后为y=(x-2)2+k,则b、k的值分别为(
)
A.0,5
B.0,1
C.-4,5
D.-4,0
5.抛物线y=x2+4x+a2+5(a是常数)的顶点在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
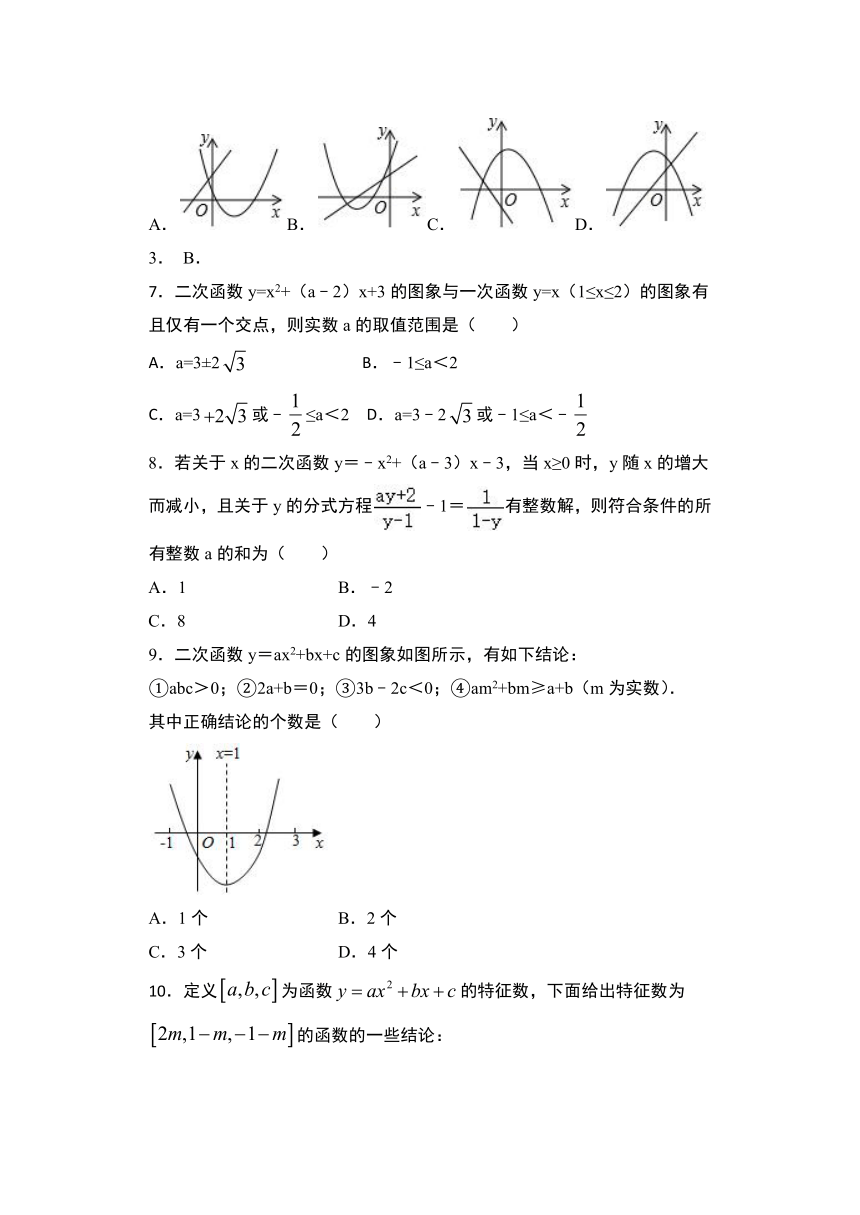
6.一次函数y=acx+b与二次函数y=ax2+bx+c在同一平面直角坐标系中的图象可能是( )
A.B.C.D.
3.
B.
7.二次函数y=x2+(a﹣2)x+3的图象与一次函数y=x(1≤x≤2)的图象有且仅有一个交点,则实数a的取值范围是( )
A.a=3±2
B.﹣1≤a<2
C.a=3或﹣≤a<2
D.a=3﹣2或﹣1≤a<﹣
8.若关于x的二次函数y=﹣x2+(a﹣3)x﹣3,当x≥0时,y随x的增大而减小,且关于y的分式方程﹣1=有整数解,则符合条件的所有整数a的和为( )
A.1
B.﹣2
C.8
D.4
9.二次函数y=ax2+bx+c的图象如图所示,有如下结论:
①abc>0;②2a+b=0;③3b﹣2c<0;④am2+bm≥a+b(m为实数).
其中正确结论的个数是( )
A.1个
B.2个
C.3个
D.4个
10.定义为函数的特征数,下面给出特征数为的函数的一些结论:
①当时,函数图象的顶点坐标是;②当时,函数图象截轴所得的线段长度大于;③当时,函数在时,随的增大而减小;④当时,函数图象经过同一个点.其中正确的结论有(
)
A.①②③④
B.①②④
C.①③④
D.②④
二、填空题
11.抛物线y=x2﹣6x+1的顶点坐标是
.
12.二次函数y=x2﹣16x﹣8的最小值是
.
13.如图,二次函数y=ax2+bx+c(a>0)的图象的顶点为点D,其图象与x轴的交点A、B的横坐标分别为-1,3,与y轴负半轴交于点C.在下面五个结论中:①2a-b=0;②a+b+c>0;③c=-3a;④只有当a=时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a的值有4个.其中正确的结论是________(只填序号).
14.如果两点A(2,a)和B(x,b)在抛物线y=x2﹣4x+m上,那么a和b的大小关系为:a
b.(从“>”“≥”“<”“≤”中选择).
15.若二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).则S=a+b+c的值的变化范围是
.
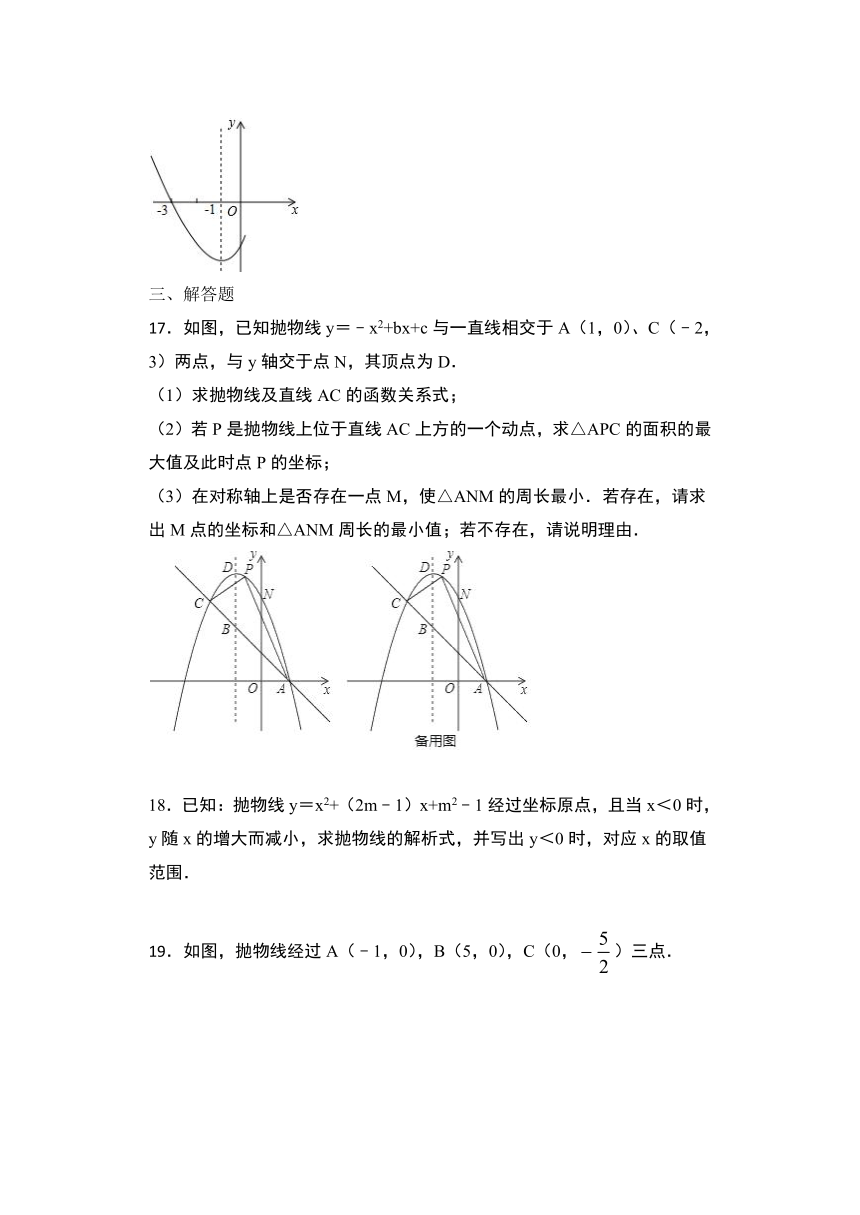
16.如图,是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=﹣1,且过点(﹣3,0),下列说法:①abc<0;②2a﹣b=0;③若(﹣5,y1),(3,y2)是抛物线上两点,则y1=y2;④4a+2b+c<0,其中说法正确的
(填写序号).
三、解答题
17.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(1,0)、C(﹣2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;
(3)在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.
18.已知:抛物线y=x2+(2m﹣1)x+m2﹣1经过坐标原点,且当x<0时,y随x的增大而减小,求抛物线的解析式,并写出y<0时,对应x的取值范围.
19.如图,抛物线经过A(﹣1,0),B(5,0),C(0,)三点.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
20.已知抛物线y=ax2﹣2ax﹣3+2a2(a≠0).
(1)求这条抛物线的对称轴;
(2)若该抛物线的顶点在x轴上,求其解析式;
(3)设点P(m,y1),Q(3,y2)在抛物线上,若y1<y2,求m的取值范围.
21.
东坡商贸公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为:
,且其日销售量y(kg)与时间t(天)的关系如下表:
时间t(天)
1
3
6
10
20
…
日销售量y(kg)
118
114
108
100
80
…
(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?
(2)问哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
答案
1.
D
2.
A
3.
B
4.
D
5.
B
6.
B
7.
D
8.
D
9.
D
10.
B
11.
(3,﹣8)
12.
﹣72.
13.
③④
14.
≤
15.
0<S<2.
16.
①②③.
17.
(1)y=﹣x2﹣2x+3;y=﹣x+1;(2)当x=﹣时,△APC的面积取最大值,最大值为,此时点P的坐标为(﹣,);(3)在对称轴上存在一点M(﹣1,2),使△ANM的周长最小,△ANM周长的最小值为3.
18.
解:∵抛物线y=x2+(2m﹣1)x+m2﹣1经过坐标原点,
∴m2﹣1=0,
∴m=±1,
∵当x<0时,y随x的增大而减小,
∴m=﹣1,
∴抛物线的解析式为y=x2﹣3x,
当y<0时,对应x的取值范围为0<x<3.
19.
(1)抛物线的解析式为:.
(2)P(2,).
(3)存在点N的坐标为(4,),(,)或(,)
20.
解:(1)∵抛物线y=ax2﹣2ax﹣3+2a2=a(x﹣1)2+2a2﹣a﹣3.
∴抛物线的对称轴为直线x=1;
(2)∵抛物线的顶点在x轴上,
∴2a2﹣a﹣3=0,
解得a=或a=﹣1,
∴抛物线为y=x2﹣3x+或y=﹣x2+2x﹣1;
(3)∵抛物线的对称轴为x=1,
则Q(3,y2)关于x=1对称点的坐标为(﹣1,y2),
∴当a>0,﹣1<m<3时,y1<y2;当a<0,m<﹣1或m>3时,y1<y2.
21.
(1)y=120?2t,60;(2)在第10天的销售利润最大,最大利润为1250元;(3)7≤n<9.
二次函数y=ax2+bx+c的图象和性质拓展练习
一、选择题
1.将抛物线y=2x2﹣1先向左平移1个单位长度,再向上平移2个单位长度,得到的抛物线的顶点坐标为( )
A.(0,﹣1)
B.(1,1)
C.(﹣1,﹣3)
D.(﹣1,1)
2.已知二次函数y=x2﹣6x+1,关于该函数在﹣1≤x≤4的取值范围内,下列说法正确的是( )
A.有最大值8,最小值﹣8
B.有最大值8,最小值﹣7C.有最大值﹣7,最小值﹣8
D.有最大值1,最小值﹣7
3.已知非负数,,满足,,设的最大值为,最小值为,则的值为(
)
A.
B.
C.
D.
4.若二次函数y=x2+bx+4配方后为y=(x-2)2+k,则b、k的值分别为(
)
A.0,5
B.0,1
C.-4,5
D.-4,0
5.抛物线y=x2+4x+a2+5(a是常数)的顶点在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
6.一次函数y=acx+b与二次函数y=ax2+bx+c在同一平面直角坐标系中的图象可能是( )
A.B.C.D.
3.
B.
7.二次函数y=x2+(a﹣2)x+3的图象与一次函数y=x(1≤x≤2)的图象有且仅有一个交点,则实数a的取值范围是( )
A.a=3±2
B.﹣1≤a<2
C.a=3或﹣≤a<2
D.a=3﹣2或﹣1≤a<﹣
8.若关于x的二次函数y=﹣x2+(a﹣3)x﹣3,当x≥0时,y随x的增大而减小,且关于y的分式方程﹣1=有整数解,则符合条件的所有整数a的和为( )
A.1
B.﹣2
C.8
D.4
9.二次函数y=ax2+bx+c的图象如图所示,有如下结论:
①abc>0;②2a+b=0;③3b﹣2c<0;④am2+bm≥a+b(m为实数).
其中正确结论的个数是( )
A.1个
B.2个
C.3个
D.4个
10.定义为函数的特征数,下面给出特征数为的函数的一些结论:
①当时,函数图象的顶点坐标是;②当时,函数图象截轴所得的线段长度大于;③当时,函数在时,随的增大而减小;④当时,函数图象经过同一个点.其中正确的结论有(
)
A.①②③④
B.①②④
C.①③④
D.②④
二、填空题
11.抛物线y=x2﹣6x+1的顶点坐标是
.
12.二次函数y=x2﹣16x﹣8的最小值是
.
13.如图,二次函数y=ax2+bx+c(a>0)的图象的顶点为点D,其图象与x轴的交点A、B的横坐标分别为-1,3,与y轴负半轴交于点C.在下面五个结论中:①2a-b=0;②a+b+c>0;③c=-3a;④只有当a=时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a的值有4个.其中正确的结论是________(只填序号).
14.如果两点A(2,a)和B(x,b)在抛物线y=x2﹣4x+m上,那么a和b的大小关系为:a
b.(从“>”“≥”“<”“≤”中选择).
15.若二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).则S=a+b+c的值的变化范围是
.
16.如图,是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=﹣1,且过点(﹣3,0),下列说法:①abc<0;②2a﹣b=0;③若(﹣5,y1),(3,y2)是抛物线上两点,则y1=y2;④4a+2b+c<0,其中说法正确的
(填写序号).
三、解答题
17.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(1,0)、C(﹣2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;
(3)在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.
18.已知:抛物线y=x2+(2m﹣1)x+m2﹣1经过坐标原点,且当x<0时,y随x的增大而减小,求抛物线的解析式,并写出y<0时,对应x的取值范围.
19.如图,抛物线经过A(﹣1,0),B(5,0),C(0,)三点.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
20.已知抛物线y=ax2﹣2ax﹣3+2a2(a≠0).
(1)求这条抛物线的对称轴;
(2)若该抛物线的顶点在x轴上,求其解析式;
(3)设点P(m,y1),Q(3,y2)在抛物线上,若y1<y2,求m的取值范围.
21.
东坡商贸公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为:
,且其日销售量y(kg)与时间t(天)的关系如下表:
时间t(天)
1
3
6
10
20
…
日销售量y(kg)
118
114
108
100
80
…
(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?
(2)问哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
答案
1.
D
2.
A
3.
B
4.
D
5.
B
6.
B
7.
D
8.
D
9.
D
10.
B
11.
(3,﹣8)
12.
﹣72.
13.
③④
14.
≤
15.
0<S<2.
16.
①②③.
17.
(1)y=﹣x2﹣2x+3;y=﹣x+1;(2)当x=﹣时,△APC的面积取最大值,最大值为,此时点P的坐标为(﹣,);(3)在对称轴上存在一点M(﹣1,2),使△ANM的周长最小,△ANM周长的最小值为3.
18.
解:∵抛物线y=x2+(2m﹣1)x+m2﹣1经过坐标原点,
∴m2﹣1=0,
∴m=±1,
∵当x<0时,y随x的增大而减小,
∴m=﹣1,
∴抛物线的解析式为y=x2﹣3x,
当y<0时,对应x的取值范围为0<x<3.
19.
(1)抛物线的解析式为:.
(2)P(2,).
(3)存在点N的坐标为(4,),(,)或(,)
20.
解:(1)∵抛物线y=ax2﹣2ax﹣3+2a2=a(x﹣1)2+2a2﹣a﹣3.
∴抛物线的对称轴为直线x=1;
(2)∵抛物线的顶点在x轴上,
∴2a2﹣a﹣3=0,
解得a=或a=﹣1,
∴抛物线为y=x2﹣3x+或y=﹣x2+2x﹣1;
(3)∵抛物线的对称轴为x=1,
则Q(3,y2)关于x=1对称点的坐标为(﹣1,y2),
∴当a>0,﹣1<m<3时,y1<y2;当a<0,m<﹣1或m>3时,y1<y2.
21.
(1)y=120?2t,60;(2)在第10天的销售利润最大,最大利润为1250元;(3)7≤n<9.
同课章节目录
