3.1.1函数的概念及其表示第3课时 课件27张PPT
文档属性
| 名称 | 3.1.1函数的概念及其表示第3课时 课件27张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 321.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-02 09:16:14 | ||
图片预览








文档简介
函数的概念及其表示
第三课时
问题1 你能说说函数有哪些表示法吗?它们各自的特点又是什么?
我们已经接触过的函数的三种表示法:解析法、列表法和图象法.
解析法,就是用数学表达式表示两个变量之间的对应关系,
列表法,就是列出表格来表示两个变量之间的对应关系,
图象法,就是用图象表示两个变量之间的对应关系,
如3.1.1的问题1、2.
如3.1.1的问题4.
如3.1.1的问题3.
复习引入
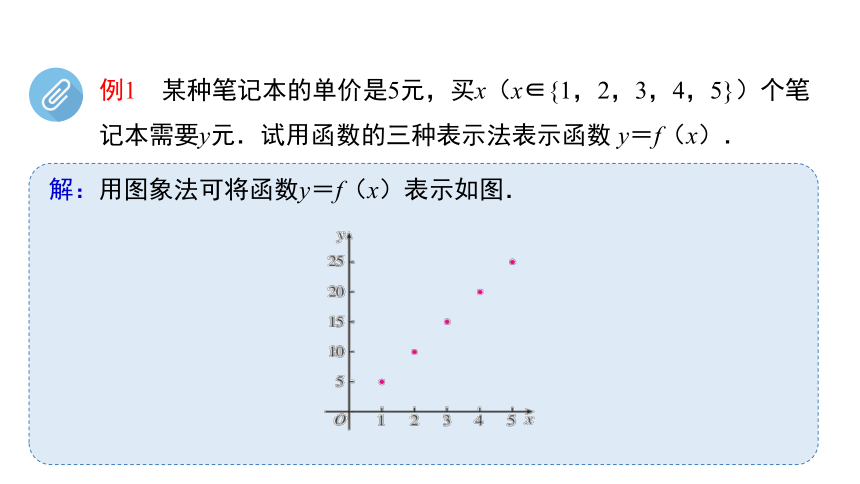
例1 某种笔记本的单价是5元,买x(x∈{1,2,3,4,5})个笔记本需要y元.试用函数的三种表示法表示函数 y=f(x).
解:这个函数的定义域是数集{1,2,3,4,5}.
用解析法可将函数y=f(x)表示为
y=5x,x∈{1,2,3,4,5}.
用列表法可将函数y=f(x)表示为
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}笔记本数x
1
2
3
4
5
钱数y
5
10
15
20
25
新知探究
解:用图象法可将函数y=f(x)表示如图.
新知探究
例1 某种笔记本的单价是5元,买x(x∈{1,2,3,4,5})个笔记本需要y元.试用函数的三种表示法表示函数 y=f(x).
追问1 你能说说这个函数与正比例函数y=5x,x∈R的异同吗?
解析式相同,定义域、值域都不同,从图象上看,
这个函数的图象是由5个离散的点构成的,
正比例函数的图象是一条连续的直线.
新知探究
追问2 比较函数的三种表示法,它们各自的特点是什么?
解析法有两个优点:
二是可以通过解析式求出任意一个自变量的值所对应的函数值;
图象法的优点是直观形象地表示随着自变量的变化,
相应的函数值变化的趋势,有利于我们研究函数的某些性质;
一是简明、全面地概括了变量间的对应关系;
列表法的优点就是不需要计算就可以直接看出与自变量的值相对应的函数值.
新知探究
追问3 所有函数都能用解析法表示吗?列表法与图象法呢?请你举出实例加以说明.
不是所有的函数都能用这三种方法表示,
有的函数只能采取某一种表示法.
比如课本3.1.1的问题3中的函数只能用图象法表示,
不能用解析法和列表法表示;
不能用图象法表示.
再比如课本第75页给出的狄利克雷函数f(x)=
新知探究
例2 画出函数y=|x|的图象.
追问1 y=|x|不属于之前学过的任何一类函数,你能将解析式变形,化为不含绝对值的形式吗?
根据绝对值的定义,分类讨论:
当x<0时,y=|x|=-x;
当x≥0时,y=|x|=x.
新知探究
追问2 如何画y=|x|的图象?
在同一直角坐标系中分别画出y=-x,
x<0和y=x,x≥0的图象,
则y=|x|的图象就是这两部分图象的组合.
新知探究
追问3 函数图象既可以是连续的曲线,也可以是直线、折线、离散的点等.那么判断一个图形是不是函数图象的依据是什么?
任意与x轴垂直的直线与图象至多一个交点.
解:由绝对值的概念,我们有
所以,函数y=|x|的图象如图所示.
y=
新知探究
例2 画出函数y=|x|的图象.
追问4 你能举出生活中可以用分段函数描述的实际问题吗?
像例2中y= 这样的函数称为分段函数.
分段函数特点:
在它的定义域中,对于自变量x的不同取值范围,对应关系不同.
如出租车的计费、天然气的计费、银行的利率等.
新知探究
例3 给定函数f(x)=x+1,g(x)=(x+1)2,x∈R,
(1)在同一直角坐标系中画出函数f(x),g(x)的图象;
(2)?x∈R,用M(x)表示f(x),g(x)中的较大者,记为
M(x)=max{f(x),g(x)}.
例如,当x=2时,M(2)=max{f(2),g(2)}=max{3,9}=9.
请分别用图象法和解析法表示函数M(x).
新知探究
追问1 如图,你能说说f(x)>g(x)对应图象上的什么特征吗?
当自变量x的取值相同时,
函数f(x)对应的点比函数g(x)对应的点高.
新知探究
追问2 你能从图象上观察并回答M(x)的取值情况吗?
当x<-1时,
g(x)=(x+1)2的图象位于f(x)=x+1的上方,
g(x)=(x+1)2为较大者,
此时M(x)=(x+1)2;
当-1<x<0时,f(x)=x+1的图象位于g(x)=(x+1)2的上方,
f(x)=x+1为较大者,此时M(x)=x+1;
新知探究
追问2 你能从图象上观察并回答M(x)的取值情况吗?
当x>0时,
g(x)=(x+1)2的图象位于f(x)=x+1的上方,
g(x)=(x+1)2为较大者,
此时M(x)=(x+1)2;
当x=-1或x=0时,g(x)=(x+1)2的图象与f(x)=x+1相交,
f(x)与g(x)相等,M(x)=f(x)=g(x).
新知探究
追问3 你能用代数方法求出M(x)=max{f(x),g(x)}的表达式吗?
令f(x)>g(x),即x+1>(x+1)2,
令g(x)>f(x),即(x+1)2>x+1,
令f(x)=g(x),即x+1=(x+1)2,
解得:-1<x<0;
解得:x<-1或x>0;
新知探究
解得:x=-1或x=0.
追问3 你能用代数方法求出M(x)=max{f(x),g(x)}的表达式吗?
新知探究
综上可得:M(x)=
例3 给定函数f(x)=x+1,g(x)=(x+1)2,x∈R,
(1)在同一直角坐标系中画出函数f(x),g(x)的图象;
(2)?x∈R,用M(x)表示f(x),g(x)中的较大者,记为
M(x)=max{f(x),g(x)}.
新知探究
解:(1)在同一直角坐标系中画出函数
图1
f(x), g(x)的图象(图1).
例3 给定函数f(x)=x+1,g(x)=(x+1)2,x∈R,
M(x)=max{f(x),g(x)}.
新知探究
(2)?x∈R,用M(x)表示f(x),g(x)中的较大者,记为
解:(2)由图1中函数取值的情况,结合函数M(x)的定义,可得函数M(x)的图象(图2).
图2
由(x+1)2=x+1,得x(x+1)=0.
解得x=-1,或x=0.
例3 给定函数f(x)=x+1,g(x)=(x+1)2,x∈R,
M(x)=max{f(x),g(x)}.
新知探究
(2)?x∈R,用M(x)表示f(x),g(x)中的较大者,记为
结合图2,得出函数M(x)的解析式为
图2
问题2 请同学们回顾本节课的内容,回答下列问题:
(1)函数常用的表示法有哪些?它们各自的特点是什么?
(2)结合本节课的学习,你对如何学习函数又有什么体会?
(1)函数常用的表示法有:解析法、表格法和图象法,
其中解析式是精确的、图象是直观的、表格是直接的;
(2)解析式、表格、图象是对应关系f的不同的表现形式,
但实质相同,为了更好地分析和解决问题,
有时需要进行不同表示法的转化和综合使用.
归纳小结
作业:教科书习题3.1第6,7,10,11,13,18题.
作业布置
1. 如图,把直截面半径为25 cm的圆形木头锯成矩形木料,如果矩形的一边长为x(单位:cm),面积为y(单位:cm2),把y表示为x的函数.
目标检测
答案:y= ,x∈(0,50).
1
2.画出函数y=|x-2|的图象.
目标检测
答案:图象如图.
2
3. 给定函数f(x)=-x+1,g(x)=(x-1)2,x∈R,
目标检测
(1)在同一直角坐标系中画出函数f(x),g(x)的图象;
(2)?x∈R,用m(x)表示f(x),g(x)中的较小者,记为
m(x)=min{f(x),g(x)},
请分别用图象法和解析法表示函数m(x).
3
解:(1)f(x),g(x)的图象如图1;
目标检测
(2)由图1得出函数m(x)的图象2,
由图2得到函数m(x)的解析式为
图1
图2
再见
第三课时
问题1 你能说说函数有哪些表示法吗?它们各自的特点又是什么?
我们已经接触过的函数的三种表示法:解析法、列表法和图象法.
解析法,就是用数学表达式表示两个变量之间的对应关系,
列表法,就是列出表格来表示两个变量之间的对应关系,
图象法,就是用图象表示两个变量之间的对应关系,
如3.1.1的问题1、2.
如3.1.1的问题4.
如3.1.1的问题3.
复习引入
例1 某种笔记本的单价是5元,买x(x∈{1,2,3,4,5})个笔记本需要y元.试用函数的三种表示法表示函数 y=f(x).
解:这个函数的定义域是数集{1,2,3,4,5}.
用解析法可将函数y=f(x)表示为
y=5x,x∈{1,2,3,4,5}.
用列表法可将函数y=f(x)表示为
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}笔记本数x
1
2
3
4
5
钱数y
5
10
15
20
25
新知探究
解:用图象法可将函数y=f(x)表示如图.
新知探究
例1 某种笔记本的单价是5元,买x(x∈{1,2,3,4,5})个笔记本需要y元.试用函数的三种表示法表示函数 y=f(x).
追问1 你能说说这个函数与正比例函数y=5x,x∈R的异同吗?
解析式相同,定义域、值域都不同,从图象上看,
这个函数的图象是由5个离散的点构成的,
正比例函数的图象是一条连续的直线.
新知探究
追问2 比较函数的三种表示法,它们各自的特点是什么?
解析法有两个优点:
二是可以通过解析式求出任意一个自变量的值所对应的函数值;
图象法的优点是直观形象地表示随着自变量的变化,
相应的函数值变化的趋势,有利于我们研究函数的某些性质;
一是简明、全面地概括了变量间的对应关系;
列表法的优点就是不需要计算就可以直接看出与自变量的值相对应的函数值.
新知探究
追问3 所有函数都能用解析法表示吗?列表法与图象法呢?请你举出实例加以说明.
不是所有的函数都能用这三种方法表示,
有的函数只能采取某一种表示法.
比如课本3.1.1的问题3中的函数只能用图象法表示,
不能用解析法和列表法表示;
不能用图象法表示.
再比如课本第75页给出的狄利克雷函数f(x)=
新知探究
例2 画出函数y=|x|的图象.
追问1 y=|x|不属于之前学过的任何一类函数,你能将解析式变形,化为不含绝对值的形式吗?
根据绝对值的定义,分类讨论:
当x<0时,y=|x|=-x;
当x≥0时,y=|x|=x.
新知探究
追问2 如何画y=|x|的图象?
在同一直角坐标系中分别画出y=-x,
x<0和y=x,x≥0的图象,
则y=|x|的图象就是这两部分图象的组合.
新知探究
追问3 函数图象既可以是连续的曲线,也可以是直线、折线、离散的点等.那么判断一个图形是不是函数图象的依据是什么?
任意与x轴垂直的直线与图象至多一个交点.
解:由绝对值的概念,我们有
所以,函数y=|x|的图象如图所示.
y=
新知探究
例2 画出函数y=|x|的图象.
追问4 你能举出生活中可以用分段函数描述的实际问题吗?
像例2中y= 这样的函数称为分段函数.
分段函数特点:
在它的定义域中,对于自变量x的不同取值范围,对应关系不同.
如出租车的计费、天然气的计费、银行的利率等.
新知探究
例3 给定函数f(x)=x+1,g(x)=(x+1)2,x∈R,
(1)在同一直角坐标系中画出函数f(x),g(x)的图象;
(2)?x∈R,用M(x)表示f(x),g(x)中的较大者,记为
M(x)=max{f(x),g(x)}.
例如,当x=2时,M(2)=max{f(2),g(2)}=max{3,9}=9.
请分别用图象法和解析法表示函数M(x).
新知探究
追问1 如图,你能说说f(x)>g(x)对应图象上的什么特征吗?
当自变量x的取值相同时,
函数f(x)对应的点比函数g(x)对应的点高.
新知探究
追问2 你能从图象上观察并回答M(x)的取值情况吗?
当x<-1时,
g(x)=(x+1)2的图象位于f(x)=x+1的上方,
g(x)=(x+1)2为较大者,
此时M(x)=(x+1)2;
当-1<x<0时,f(x)=x+1的图象位于g(x)=(x+1)2的上方,
f(x)=x+1为较大者,此时M(x)=x+1;
新知探究
追问2 你能从图象上观察并回答M(x)的取值情况吗?
当x>0时,
g(x)=(x+1)2的图象位于f(x)=x+1的上方,
g(x)=(x+1)2为较大者,
此时M(x)=(x+1)2;
当x=-1或x=0时,g(x)=(x+1)2的图象与f(x)=x+1相交,
f(x)与g(x)相等,M(x)=f(x)=g(x).
新知探究
追问3 你能用代数方法求出M(x)=max{f(x),g(x)}的表达式吗?
令f(x)>g(x),即x+1>(x+1)2,
令g(x)>f(x),即(x+1)2>x+1,
令f(x)=g(x),即x+1=(x+1)2,
解得:-1<x<0;
解得:x<-1或x>0;
新知探究
解得:x=-1或x=0.
追问3 你能用代数方法求出M(x)=max{f(x),g(x)}的表达式吗?
新知探究
综上可得:M(x)=
例3 给定函数f(x)=x+1,g(x)=(x+1)2,x∈R,
(1)在同一直角坐标系中画出函数f(x),g(x)的图象;
(2)?x∈R,用M(x)表示f(x),g(x)中的较大者,记为
M(x)=max{f(x),g(x)}.
新知探究
解:(1)在同一直角坐标系中画出函数
图1
f(x), g(x)的图象(图1).
例3 给定函数f(x)=x+1,g(x)=(x+1)2,x∈R,
M(x)=max{f(x),g(x)}.
新知探究
(2)?x∈R,用M(x)表示f(x),g(x)中的较大者,记为
解:(2)由图1中函数取值的情况,结合函数M(x)的定义,可得函数M(x)的图象(图2).
图2
由(x+1)2=x+1,得x(x+1)=0.
解得x=-1,或x=0.
例3 给定函数f(x)=x+1,g(x)=(x+1)2,x∈R,
M(x)=max{f(x),g(x)}.
新知探究
(2)?x∈R,用M(x)表示f(x),g(x)中的较大者,记为
结合图2,得出函数M(x)的解析式为
图2
问题2 请同学们回顾本节课的内容,回答下列问题:
(1)函数常用的表示法有哪些?它们各自的特点是什么?
(2)结合本节课的学习,你对如何学习函数又有什么体会?
(1)函数常用的表示法有:解析法、表格法和图象法,
其中解析式是精确的、图象是直观的、表格是直接的;
(2)解析式、表格、图象是对应关系f的不同的表现形式,
但实质相同,为了更好地分析和解决问题,
有时需要进行不同表示法的转化和综合使用.
归纳小结
作业:教科书习题3.1第6,7,10,11,13,18题.
作业布置
1. 如图,把直截面半径为25 cm的圆形木头锯成矩形木料,如果矩形的一边长为x(单位:cm),面积为y(单位:cm2),把y表示为x的函数.
目标检测
答案:y= ,x∈(0,50).
1
2.画出函数y=|x-2|的图象.
目标检测
答案:图象如图.
2
3. 给定函数f(x)=-x+1,g(x)=(x-1)2,x∈R,
目标检测
(1)在同一直角坐标系中画出函数f(x),g(x)的图象;
(2)?x∈R,用m(x)表示f(x),g(x)中的较小者,记为
m(x)=min{f(x),g(x)},
请分别用图象法和解析法表示函数m(x).
3
解:(1)f(x),g(x)的图象如图1;
目标检测
(2)由图1得出函数m(x)的图象2,
由图2得到函数m(x)的解析式为
图1
图2
再见
