3.1.1函数的概念及其表示第2课时 课件26张PPT
文档属性
| 名称 | 3.1.1函数的概念及其表示第2课时 课件26张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 261.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-02 09:15:01 | ||
图片预览








文档简介
函数的概念及其表示
第二课时
问题1 在上一小节里,我们重新学习了函数的概念,请你默写这个概念.
对于数集A中的任意一个数x,按照某种确定的对应关系f,在集合B中都有唯一确定的数y和它对应,那么就称f:A→B为从集合A到集合B的一个函数,记作
y=f(x),x∈A.
其中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y值叫做函数值,函数值的集合{f(x)|x∈A}叫做函数的值域.
复习引入
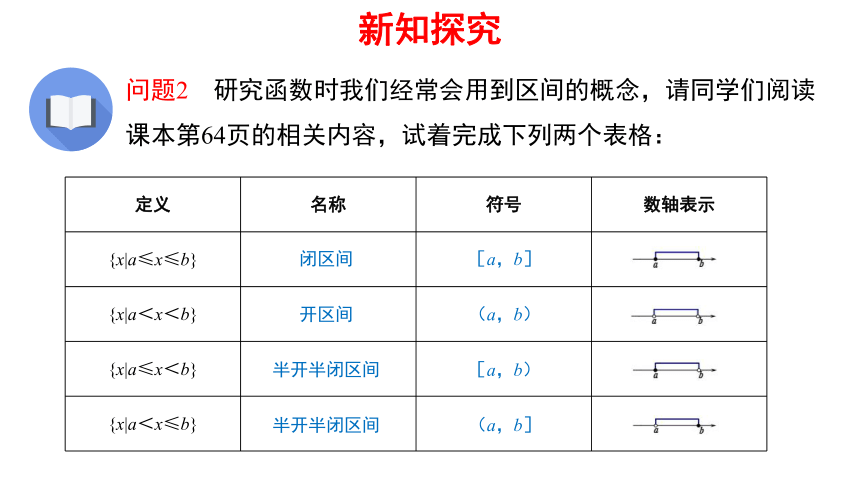
问题2 研究函数时我们经常会用到区间的概念,请同学们阅读课本第64页的相关内容,试着完成下列两个表格:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}定义
名称
符号
数轴表示
{x|a≤x≤b}
{x|a<x<b}
{x|a≤x<b}
{x|a<x≤b}
闭区间
开区间
半开半闭区间
半开半闭区间
[a,b]
(a,b)
[a,b)
(a,b]
新知探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}定义
名称
数轴表示
{x|x≥a}
{x|x>a}
{x|x≤b}
{x|x<b}
[a,+∞)
(a,+∞)
(-∞,b]
(-∞,b)
新知探究
问题2 研究函数时我们经常会用到区间的概念,请同学们阅读课本第64页的相关内容,试着完成下列两个表格:
追问1 区间的左端点a与右端点b的关系是什么?
a<b.
追问2 区间与数轴之间的关系是什么?
任何区间均可在数轴上表示出来,区间中的每个元素对应数轴上的一个点.
追问3 学习区间的意义是什么?
区间表示连续性的数集,为我们研究函数的定义域、值域提供方便.
新知探究
例1 已知函数f(x)= ,
(1)求函数f(x)的定义域;
(2)求f(-3),f( )的值;
(3)当a>0时,求f(a),f(a-1)的值.
解得:x≥-3且x≠-2.
所以函数f(x)的定义域为[-3,-2)∪(-2,+∞).
解:(1)要使该函数有意义,则需
新知探究
(2)求f(-3),f( )的值;
解:(2)将-3与 代入解析式,有
新知探究
例1 已知函数f(x)= ,
(3)当a>0时,求f(a),f(a-1)的值.
解:(3)因为a>0时,所以f(a),f(a-1)有意义.
新知探究
例1 已知函数f(x)= ,
追问1 如何求解函数的定义域?
当已知解析式 y=f(x),
那么函数的定义域就是指能使这个式子有意义的实数的集合.
比如:①偶次方根中被开方数非负;
②分式中分母不能为0;
③0次幂式中底数不能为0;
④在实际问题中,还必须考虑自变量所代表的具体量的允许值范围.
新知探究
追问2 f(x)= 与y= 的含义相同,都是给出了一个函数的解析式,用f(x)替换y之后有什么优势?
在y= 中,要表示-3对应的函数值,
我们一般都需要这样描述:当x=-3时,y=-1;
而在f(x)= 中,我们只需要用 f(-3)=-1表示即可.
新知探究
追问3 f(x)与f(a)有何区别与联系?
f(a)表示当自变量x=a时的函数值,是一个确定的数,
而f(x)表示变量,f(a)是f(x)的一个特殊值.
新知探究
追问4 能说说你对记号“y=f(x)”的理解吗?
在同时研究两个或多个函数时,常用不同符号表示不同的函数,除用符号f(x)外,还常用g(x)、F(x)、G(x)等符号来表示.
首先它不能理解为“y等于f与x的乘积”,
它是“y是x的函数”的符号表示,
具体而言是:变量x在对应关系f的作用下对应到y.
新知探究
例2 下列函数中哪个与函数y=x是同一个函数?
(1) ; (2) ;
(3) ; (4) .
解:(1) (x∈[0,+∞)),
它与函数y=x(x∈R)虽然对应关系相同,
但是定义域不相同,
所以这个函数与函数y=x(x∈R)不是同一个函数.
新知探究
(1) ; (2) ;
(3) ; (4) .
解:(2) (v∈R),
它与函数y=x(x∈R)不仅对应关系相同,
而且定义域也相同,
所以这个函数与函数y=x(x∈R)是同一个函数.
新知探究
例2 下列函数中哪个与函数y=x是同一个函数?
(1) ; (2) ;
(3) ; (4) .
解: (3)
它与函数y=x(x∈R)虽然定义域都是实数集R,
但是当x<0时,它的对应关系与y=x(x∈R)不相同,
所以这个函数与函数y=x(x∈R)不是同一个函数.
新知探究
例2 下列函数中哪个与函数y=x是同一个函数?
例2 下列函数中哪个与函数y=x是同一个函数?
(1) ; (2) ;
(3) ; (4) .
解: (4) (n∈(-∞,0)∪(0,+∞)),
它与函数y=x(x∈R)的对应关系相同但定义域不相同,
所以这个函数与函数y=x(x∈R)不是同一个函数.
新知探究
追问1 两个函数相等的含义是什么?
函数的三要素都相等.
值域是由定义域和对应关系决定的,
所以只要两个函数的定义域和对应关系一致,这两个函数就相等.
新知探究
追问2 你能总结判断两个函数是否相同的步骤吗?
先求函数的定义域,如果定义域不相同,
则不是相同函数,结束判断;
如果相等,则判断对应关系是否相同,
定义域和对应关系均相等才能得出相等的结论.
新知探究
追问3 你如何理解函数u= 的对应关系?
所以对于R中的任一实数v,
通过对应关系u=v,在R中都有唯一的一个实数u与之对应,
因为u=v,所以就是任一实数与它本身的对应.
因为u= =v(v∈R),
新知探究
追问4 你能结合函数的图象验证你的判断吗?
只有图(2)中的图象与y=x的图象完全相同.
新知探究
问题3 请同学们回顾本节课的内容,回答下列问题:
归纳小结
(1)区间是表示什么的符号?
(2)在判断两个函数是否相同时,我们需要注意什么?
区间是用于表示连续数集的符号.
定义域相同是函数相等的先决条件,需要优先判断;对应关系相等与否不在于解析式用什么字母符号表示,而在于同一自变量对应的函数值是否相等.
作业:教科书习题3.1第2,4,5,17题.
作业布置
求下列函数的定义域:
目标检测
(1)f(x)= ; (2)f(x)= .
答案:(1)(-∞,- )∪(- ,+∞);(2)[-3,1].
1
目标检测
已知函数f(x)=3x3+2x,
(1)求f(2),f(-2),f(2)+f(-2)的值;
(2)求f(a),f(-a),f(a)+f(-a)的值.
答案:(1)f(2)=28,f(-2)=-28,f(2)+f(-2)=0;
(2)f(a)=3a3+2a,f(-a)=-3a3-2a,
f(a)+f(-a)=0.
2
判断下列各组中的函数是否为同一个函数,并说明理由:
目标检测
(1)表示炮弹飞行高度h与时间t关系的函数h=130t-5t2和二次函数y=130x-5x2;
(2)f(x)=1和g(x)=x0.
答案: (1)不相同,
因为前者的定义域为R,
后者的定义域为R;
(2)不相同,
后者的定义域为(-∞,0)∪(0,+∞).
因为前者的定义域为[0,26],
3
再见
第二课时
问题1 在上一小节里,我们重新学习了函数的概念,请你默写这个概念.
对于数集A中的任意一个数x,按照某种确定的对应关系f,在集合B中都有唯一确定的数y和它对应,那么就称f:A→B为从集合A到集合B的一个函数,记作
y=f(x),x∈A.
其中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y值叫做函数值,函数值的集合{f(x)|x∈A}叫做函数的值域.
复习引入
问题2 研究函数时我们经常会用到区间的概念,请同学们阅读课本第64页的相关内容,试着完成下列两个表格:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}定义
名称
符号
数轴表示
{x|a≤x≤b}
{x|a<x<b}
{x|a≤x<b}
{x|a<x≤b}
闭区间
开区间
半开半闭区间
半开半闭区间
[a,b]
(a,b)
[a,b)
(a,b]
新知探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}定义
名称
数轴表示
{x|x≥a}
{x|x>a}
{x|x≤b}
{x|x<b}
[a,+∞)
(a,+∞)
(-∞,b]
(-∞,b)
新知探究
问题2 研究函数时我们经常会用到区间的概念,请同学们阅读课本第64页的相关内容,试着完成下列两个表格:
追问1 区间的左端点a与右端点b的关系是什么?
a<b.
追问2 区间与数轴之间的关系是什么?
任何区间均可在数轴上表示出来,区间中的每个元素对应数轴上的一个点.
追问3 学习区间的意义是什么?
区间表示连续性的数集,为我们研究函数的定义域、值域提供方便.
新知探究
例1 已知函数f(x)= ,
(1)求函数f(x)的定义域;
(2)求f(-3),f( )的值;
(3)当a>0时,求f(a),f(a-1)的值.
解得:x≥-3且x≠-2.
所以函数f(x)的定义域为[-3,-2)∪(-2,+∞).
解:(1)要使该函数有意义,则需
新知探究
(2)求f(-3),f( )的值;
解:(2)将-3与 代入解析式,有
新知探究
例1 已知函数f(x)= ,
(3)当a>0时,求f(a),f(a-1)的值.
解:(3)因为a>0时,所以f(a),f(a-1)有意义.
新知探究
例1 已知函数f(x)= ,
追问1 如何求解函数的定义域?
当已知解析式 y=f(x),
那么函数的定义域就是指能使这个式子有意义的实数的集合.
比如:①偶次方根中被开方数非负;
②分式中分母不能为0;
③0次幂式中底数不能为0;
④在实际问题中,还必须考虑自变量所代表的具体量的允许值范围.
新知探究
追问2 f(x)= 与y= 的含义相同,都是给出了一个函数的解析式,用f(x)替换y之后有什么优势?
在y= 中,要表示-3对应的函数值,
我们一般都需要这样描述:当x=-3时,y=-1;
而在f(x)= 中,我们只需要用 f(-3)=-1表示即可.
新知探究
追问3 f(x)与f(a)有何区别与联系?
f(a)表示当自变量x=a时的函数值,是一个确定的数,
而f(x)表示变量,f(a)是f(x)的一个特殊值.
新知探究
追问4 能说说你对记号“y=f(x)”的理解吗?
在同时研究两个或多个函数时,常用不同符号表示不同的函数,除用符号f(x)外,还常用g(x)、F(x)、G(x)等符号来表示.
首先它不能理解为“y等于f与x的乘积”,
它是“y是x的函数”的符号表示,
具体而言是:变量x在对应关系f的作用下对应到y.
新知探究
例2 下列函数中哪个与函数y=x是同一个函数?
(1) ; (2) ;
(3) ; (4) .
解:(1) (x∈[0,+∞)),
它与函数y=x(x∈R)虽然对应关系相同,
但是定义域不相同,
所以这个函数与函数y=x(x∈R)不是同一个函数.
新知探究
(1) ; (2) ;
(3) ; (4) .
解:(2) (v∈R),
它与函数y=x(x∈R)不仅对应关系相同,
而且定义域也相同,
所以这个函数与函数y=x(x∈R)是同一个函数.
新知探究
例2 下列函数中哪个与函数y=x是同一个函数?
(1) ; (2) ;
(3) ; (4) .
解: (3)
它与函数y=x(x∈R)虽然定义域都是实数集R,
但是当x<0时,它的对应关系与y=x(x∈R)不相同,
所以这个函数与函数y=x(x∈R)不是同一个函数.
新知探究
例2 下列函数中哪个与函数y=x是同一个函数?
例2 下列函数中哪个与函数y=x是同一个函数?
(1) ; (2) ;
(3) ; (4) .
解: (4) (n∈(-∞,0)∪(0,+∞)),
它与函数y=x(x∈R)的对应关系相同但定义域不相同,
所以这个函数与函数y=x(x∈R)不是同一个函数.
新知探究
追问1 两个函数相等的含义是什么?
函数的三要素都相等.
值域是由定义域和对应关系决定的,
所以只要两个函数的定义域和对应关系一致,这两个函数就相等.
新知探究
追问2 你能总结判断两个函数是否相同的步骤吗?
先求函数的定义域,如果定义域不相同,
则不是相同函数,结束判断;
如果相等,则判断对应关系是否相同,
定义域和对应关系均相等才能得出相等的结论.
新知探究
追问3 你如何理解函数u= 的对应关系?
所以对于R中的任一实数v,
通过对应关系u=v,在R中都有唯一的一个实数u与之对应,
因为u=v,所以就是任一实数与它本身的对应.
因为u= =v(v∈R),
新知探究
追问4 你能结合函数的图象验证你的判断吗?
只有图(2)中的图象与y=x的图象完全相同.
新知探究
问题3 请同学们回顾本节课的内容,回答下列问题:
归纳小结
(1)区间是表示什么的符号?
(2)在判断两个函数是否相同时,我们需要注意什么?
区间是用于表示连续数集的符号.
定义域相同是函数相等的先决条件,需要优先判断;对应关系相等与否不在于解析式用什么字母符号表示,而在于同一自变量对应的函数值是否相等.
作业:教科书习题3.1第2,4,5,17题.
作业布置
求下列函数的定义域:
目标检测
(1)f(x)= ; (2)f(x)= .
答案:(1)(-∞,- )∪(- ,+∞);(2)[-3,1].
1
目标检测
已知函数f(x)=3x3+2x,
(1)求f(2),f(-2),f(2)+f(-2)的值;
(2)求f(a),f(-a),f(a)+f(-a)的值.
答案:(1)f(2)=28,f(-2)=-28,f(2)+f(-2)=0;
(2)f(a)=3a3+2a,f(-a)=-3a3-2a,
f(a)+f(-a)=0.
2
判断下列各组中的函数是否为同一个函数,并说明理由:
目标检测
(1)表示炮弹飞行高度h与时间t关系的函数h=130t-5t2和二次函数y=130x-5x2;
(2)f(x)=1和g(x)=x0.
答案: (1)不相同,
因为前者的定义域为R,
后者的定义域为R;
(2)不相同,
后者的定义域为(-∞,0)∪(0,+∞).
因为前者的定义域为[0,26],
3
再见
