《2.1.2 一元二次方程的解集及其根与系数的关系》第1课时 课件20张PPT
文档属性
| 名称 | 《2.1.2 一元二次方程的解集及其根与系数的关系》第1课时 课件20张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 191.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-02 00:00:00 | ||
图片预览








文档简介
2.1.2 一元二次方程的解集及其根与系数的关系
第1课时
问题1 阅读课本第47~49页,回答下列问题:
整体概览
(1)本节将要研究一元二次方程的解集.(2)起点是一次方程的解集以及因式分解法解一元二次方程,目标是会用配方法以及公式法求解一元二次方程或可化为一元二次方程的方程;提升数学建模素养.
(1)本节将要研究哪类问题?
(2)本节要研究的问题在数学中的地位是怎样的?
情境与问题
《九章算术》是中国古代张苍、耿寿昌所撰写的一部数学专著.是《算经十书》中最重要的一部,成于公元一世纪左右.《九章算术》内容十分丰富,全书总结了战国、秦、汉时期的数学成就.同时,《九章算术》在数学上还有其独到的成就,不仅最早提到分数问题,也首先记录了盈不足等问题,《方程》章还在世界数学史上首次阐述了负数及其加减运算法则.它是一本综合性的历史著作,是当时世界上最简练有效的应用数学,它的出现标志中国古代数学形成了完整的体系.
情境与问题
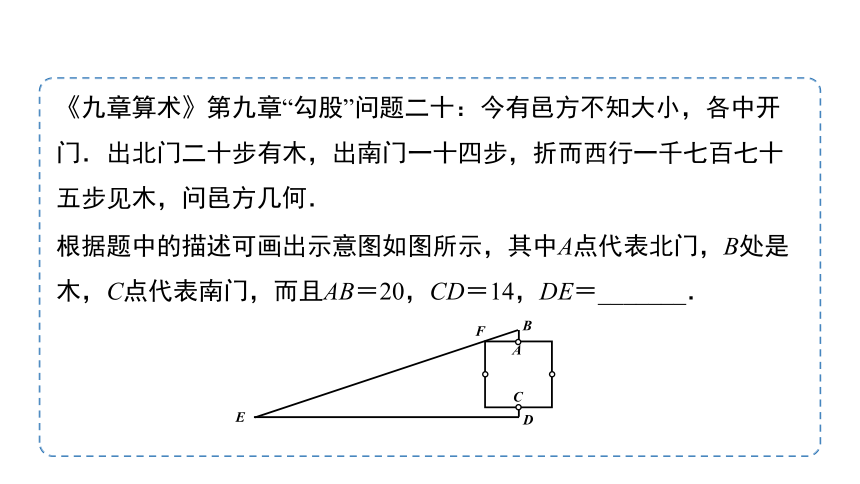
《九章算术》第九章“勾股”问题二十:今有邑方不知大小,各中开门.出北门二十步有木,出南门一十四步,折而西行一千七百七十五步见木,问邑方几何.
根据题中的描述可画出示意图如图所示,其中A点代表北门,B处是木,C点代表南门,而且AB=20,CD=14,DE=_______.
A
B
C
D
E
F
情境与问题
如果设正方形的边长为x.则有AF= ,DB=20+x+14=x+34.
根据ΔABF∽ΔDBE可知 ,从而AF·DB=AB·DE,因此
整理得x2+34x-71000=0,你会解这个方程吗?
A
B
C
D
E
F
新知探究
问题1 从上一节的内容可知,用因式分解法能得到一元二次方程的解集,但是用这种方法有时候并不容易,例如情境与问题中所得到的方程就是这种情形,此时该怎么办呢?
追问1:你认为最简单的一元二次方程具有什么样的形式?可以怎样得到这种方程的解集?举例说明.
新知探究
【练一练】方程x2=3的解集为__________;方程x2=0的解集为__________;方程x2=-2的解集为__________.
{0}
?
一般地,方程x2=t:(1)当t>0时,解集为__________;
(3)当t<0时,解集为__________.
(2)当t=0时,解集为__________;
{0}
?
追问2:形如(x-k)2=t(其中k,t是常数)的一元二次方程的解集如何得到?
新知探究
一般地,方程(x-k)2=t:
当t>0时,解集为______________;当t=0时,解集为___________;当t<0时,解集为___________.
{k}
?
【练一练】方程(x-1)2=2的解集为______________.
新知探究
结论:对于一般的一元二次方程来说,只需要将其化为(x-k)2=t的形式,就可得到方程的解集.
【练一练】方程(x-1)2=2的解集为______________.
追问3:怎样将x2+2x+3=0化为(x-k)2=t的形式?动手试试看,并写出这个方程的解集.
情境与问题
利用配方法,总是可以将ax2+bx+c=0(a≠0)化为(x-k)2=t的形式,过程如下:
因为a≠0,所以
情境与问题
因此,ax2+bx+c=0(a≠0)可以化为
从而可知,Δ=b2-4ac的符号情况决定了上述方程的解集情况:
(1)当Δ=b2-4ac>0时,方程的解集为
情境与问题
(2)当Δ=b2-4ac=0时,方程的解集为
(3)当Δ=b2-4ac<0时,方程的解集为?.
一般地,Δ=b2-4ac称为一元二次方程ax2+bx+c=0(a≠0)的判别式.由此可知,一元二次方程解集的情况完全由它的系数决定.
新知探究
例1 求下列方程的解集.
(1)x(2x-4)=5-8x; (2)(5x-3)(x+1)=(x+1)2+5;
(3)ax2+x+2=0(a≠0).
(1)方程可化为:2x2+4x-5=0,a=2,b=4,c=-5,则b2-4ac=56,
则 ,
所以原方程的解集为
新知探究
例1 求下列方程的解集.
(1)x(2x-4)=5-8x; (2)(5x-3)(x+1)=(x+1)2+5;
(3)ax2+x+2=0(a≠0).
(2)方程可化为:4x2-9=0,则
所以原方程的解集为 ;
新知探究
例1 求下列方程的解集.
(3)ax2+x+2=0(a≠0).
(3)Δ=12-4a·2=1-8a,
当a< 时,原方程的解集为 ;
当a= 时,原方程的解集为 ;
当a> 时,原方程的解集为?.
新知探究
例2 求下列方程的解集.
(1)x- -1=0
(2)(x2+3x)2+2(x2+3x)-3=0.
(1)设 =y,则y≥0,且原方程可变为y2-2y-1=0,
因此可知y=1+ 或y=1- (舍)
从而 =1+ ,即x=3+ ,所以原方程的解集为 .
新知探究
例2 求下列方程的解集.
(1)x- -1=0
(2)(x2+3x)2+2(x2+3x)-3=0.
(2)设x2+3x=y,方程化为y2+2y-3=0,即(y-1)(y+3)=0,
解得y1=1,y2=-3,即x2+3x=1或x2+3x=-3.
即x2+3x-1=0或x2+3x+3=0.
解得 ,所以原方程的解集为 .
归纳小结
回顾本节课,你有什么收获?
(1)什么叫一元二次方程?试写出一元二次方程的一般形式.
(2)如何求一元二次方程的解集?
作业:教科书P51练习B 1、4、5.
作业布置
再见
第1课时
问题1 阅读课本第47~49页,回答下列问题:
整体概览
(1)本节将要研究一元二次方程的解集.(2)起点是一次方程的解集以及因式分解法解一元二次方程,目标是会用配方法以及公式法求解一元二次方程或可化为一元二次方程的方程;提升数学建模素养.
(1)本节将要研究哪类问题?
(2)本节要研究的问题在数学中的地位是怎样的?
情境与问题
《九章算术》是中国古代张苍、耿寿昌所撰写的一部数学专著.是《算经十书》中最重要的一部,成于公元一世纪左右.《九章算术》内容十分丰富,全书总结了战国、秦、汉时期的数学成就.同时,《九章算术》在数学上还有其独到的成就,不仅最早提到分数问题,也首先记录了盈不足等问题,《方程》章还在世界数学史上首次阐述了负数及其加减运算法则.它是一本综合性的历史著作,是当时世界上最简练有效的应用数学,它的出现标志中国古代数学形成了完整的体系.
情境与问题
《九章算术》第九章“勾股”问题二十:今有邑方不知大小,各中开门.出北门二十步有木,出南门一十四步,折而西行一千七百七十五步见木,问邑方几何.
根据题中的描述可画出示意图如图所示,其中A点代表北门,B处是木,C点代表南门,而且AB=20,CD=14,DE=_______.
A
B
C
D
E
F
情境与问题
如果设正方形的边长为x.则有AF= ,DB=20+x+14=x+34.
根据ΔABF∽ΔDBE可知 ,从而AF·DB=AB·DE,因此
整理得x2+34x-71000=0,你会解这个方程吗?
A
B
C
D
E
F
新知探究
问题1 从上一节的内容可知,用因式分解法能得到一元二次方程的解集,但是用这种方法有时候并不容易,例如情境与问题中所得到的方程就是这种情形,此时该怎么办呢?
追问1:你认为最简单的一元二次方程具有什么样的形式?可以怎样得到这种方程的解集?举例说明.
新知探究
【练一练】方程x2=3的解集为__________;方程x2=0的解集为__________;方程x2=-2的解集为__________.
{0}
?
一般地,方程x2=t:(1)当t>0时,解集为__________;
(3)当t<0时,解集为__________.
(2)当t=0时,解集为__________;
{0}
?
追问2:形如(x-k)2=t(其中k,t是常数)的一元二次方程的解集如何得到?
新知探究
一般地,方程(x-k)2=t:
当t>0时,解集为______________;当t=0时,解集为___________;当t<0时,解集为___________.
{k}
?
【练一练】方程(x-1)2=2的解集为______________.
新知探究
结论:对于一般的一元二次方程来说,只需要将其化为(x-k)2=t的形式,就可得到方程的解集.
【练一练】方程(x-1)2=2的解集为______________.
追问3:怎样将x2+2x+3=0化为(x-k)2=t的形式?动手试试看,并写出这个方程的解集.
情境与问题
利用配方法,总是可以将ax2+bx+c=0(a≠0)化为(x-k)2=t的形式,过程如下:
因为a≠0,所以
情境与问题
因此,ax2+bx+c=0(a≠0)可以化为
从而可知,Δ=b2-4ac的符号情况决定了上述方程的解集情况:
(1)当Δ=b2-4ac>0时,方程的解集为
情境与问题
(2)当Δ=b2-4ac=0时,方程的解集为
(3)当Δ=b2-4ac<0时,方程的解集为?.
一般地,Δ=b2-4ac称为一元二次方程ax2+bx+c=0(a≠0)的判别式.由此可知,一元二次方程解集的情况完全由它的系数决定.
新知探究
例1 求下列方程的解集.
(1)x(2x-4)=5-8x; (2)(5x-3)(x+1)=(x+1)2+5;
(3)ax2+x+2=0(a≠0).
(1)方程可化为:2x2+4x-5=0,a=2,b=4,c=-5,则b2-4ac=56,
则 ,
所以原方程的解集为
新知探究
例1 求下列方程的解集.
(1)x(2x-4)=5-8x; (2)(5x-3)(x+1)=(x+1)2+5;
(3)ax2+x+2=0(a≠0).
(2)方程可化为:4x2-9=0,则
所以原方程的解集为 ;
新知探究
例1 求下列方程的解集.
(3)ax2+x+2=0(a≠0).
(3)Δ=12-4a·2=1-8a,
当a< 时,原方程的解集为 ;
当a= 时,原方程的解集为 ;
当a> 时,原方程的解集为?.
新知探究
例2 求下列方程的解集.
(1)x- -1=0
(2)(x2+3x)2+2(x2+3x)-3=0.
(1)设 =y,则y≥0,且原方程可变为y2-2y-1=0,
因此可知y=1+ 或y=1- (舍)
从而 =1+ ,即x=3+ ,所以原方程的解集为 .
新知探究
例2 求下列方程的解集.
(1)x- -1=0
(2)(x2+3x)2+2(x2+3x)-3=0.
(2)设x2+3x=y,方程化为y2+2y-3=0,即(y-1)(y+3)=0,
解得y1=1,y2=-3,即x2+3x=1或x2+3x=-3.
即x2+3x-1=0或x2+3x+3=0.
解得 ,所以原方程的解集为 .
归纳小结
回顾本节课,你有什么收获?
(1)什么叫一元二次方程?试写出一元二次方程的一般形式.
(2)如何求一元二次方程的解集?
作业:教科书P51练习B 1、4、5.
作业布置
再见
