《2.1.2 一元二次方程的解集及其根与系数的关系》第2课时 课件21张PPT
文档属性
| 名称 | 《2.1.2 一元二次方程的解集及其根与系数的关系》第2课时 课件21张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 163.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-02 00:00:00 | ||
图片预览








文档简介
2.1.2 一元二次方程的解集及其根与系数的关系
第2课时
问题1 阅读课本第47~49页,回答下列问题:
整体概览
(1)本节将要研究一元二次方程的根与系数的关系.(2)起点是一元二次方程的解法及求根公式,目标是会求解一元二次方程的两根和与两根积,并灵活运用根与系数的关系解决问题.提升数学运算素养.
(1)本节将要研究哪类问题?
(2)本节要研究的问题在数学中的地位是怎样的?
情境与问题
学完一元二次方程的解集后,我就听到了咱班的小奕和小涵的一段悄悄话,内容如下:
小奕:小涵,我发现了一个秘密!
小涵:什么秘密?
小奕:你知道咱们尊敬的刘老师的年龄吗?
小涵:不知道哎!
情境与问题
小奕:呵呵,这绝对是个秘密,我不能直接告诉你,我这么说吧:她的年龄是一元二次方程x2-13x+36=0的两根的积,回去你把两根求出来就知道了.
小涵:咳,这你可难不住我,我不用求根就已经知道答案了,而且我还告诉你,刘老师的年龄是方程x2-36x-40=0的两根的和呢.
小奕:哈哈,你太有才了.对了,咱们应该也让同学们猜一猜,不解方程,能不能求出刘老师的年龄.
新知探究
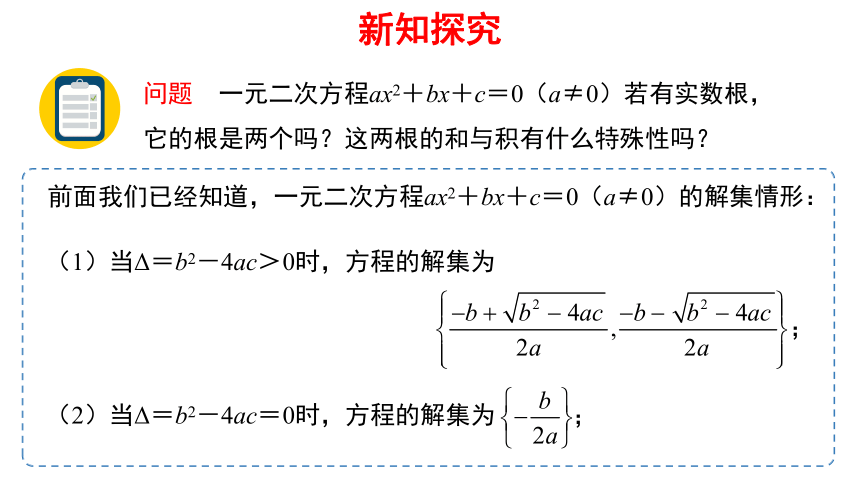
问题 一元二次方程ax2+bx+c=0(a≠0)若有实数根,它的根是两个吗?这两根的和与积有什么特殊性吗?
前面我们已经知道,一元二次方程ax2+bx+c=0(a≠0)的解集情形:
(1)当Δ=b2-4ac>0时,方程的解集为
(2)当Δ=b2-4ac=0时,方程的解集为
新知探究
问题 一元二次方程ax2+bx+c=0(a≠0)若有实数根,它的根是两个吗?这两根的和与积有什么特殊性吗?
(3)当Δ=b2-4ac<0时,方程的解集为?.
当Δ=b2-4ac≥0时,方程ax2+bx+c=0(a≠0)有两个实数根(当Δ=0时,x1=x2,按照初中的习惯,我们仍称方程有两个相等的实数根),计算可得:这两个实数根的和与积分别为
新知探究
问题 一元二次方程ax2+bx+c=0(a≠0)若有实数根,它的根是两个吗?这两根的和与积有什么特殊性吗?
(1)用语言叙述为:一元二次方程的解集不空时,两根之和为一次项系数与二次项系数之比的相反数;两根之积为常数项与二次项系数之比.
(2)ax2+bx+c=0(a≠0)的两根是x1,x2,用式子表示为:x1+x2= ,x1x2= .这个结论通常称为一元二次方程根与系数的关系.
新知探究
【数学文化】法国数学家弗朗索瓦·韦达在著作《论方程的识别与订正》中建立了方程根与系数的关系,提出了这条定理.??由于韦达最早发现代数方程的根与系数之间有这种关系,人们把这个关系称为韦达定理.
新知探究
例1 已知一元二次方程2x2+3x-4=0的两根为x1与x2,求下列各式的值:
(1)x12+x22; (2)|x1-x2|.
问题:是否要求出x1和x2,并由此给出上述(1)和(2)的答案?
新知探究
由一元二次方程根与系数的关系,得x1+x2= ,x1x2=-2,
(1)由上有x12+x22=(x1+x2)2-2x1x2
=( )2-2×(-2)
(2)因为(x1-x2)2=(x1+x2)2-4x1x2
=( )2-4×(-2)
所以|x1-x2|= .
新知探究
例2 已知关于x的一元二次方程mx2-(m+2)x+ =0有两个不相等的实数根x1,x2.若 =4m,试求m的值.
由题知 ,
解得m>-1且m≠0.
因为x1+x2= ,x1x2= ,
所以 ,
解得m=2或m=-1.
又因为m>-1,所以m=2.
新知探究
例3 已知方程x2+tx+1=0,根据下列条件,分别求出t的取值范围.
(1)两个根都大于0;
(2)两个根都小于0;
设方程x2+tx+1=0的两个根为x1,x2.
所以t的取值范围为(-∞,-2].
(1)由题意得 ,解得t≤-2.
新知探究
例3 已知方程x2+tx+1=0,根据下列条件,分别求出t的取值范围.
(1)两个根都大于0;
(2)两个根都小于0;
设方程x2+tx+1=0的两个根为x1,x2.
所以t的取值范围为[2,+∞).
(2) ,解得t≥2.
新知探究
【想一想】是否存在t,使方程x2+tx+1=0一个根大于0,另一个根小于0.
由前面知道:若有解,两根积为1是正数,所以不可能两根异号的,即不存在实数t使得方程的一个根大于0,另一个根小于0.
新知探究
已知x1,x2是一元二次方程x2-3x-1=0的两个实数根,求x12+x22+4x1x2的值.
1
根据一元二次方程根与系数的关系可知x1+x2=3,x1x2=-1.
所以x12+x22+4x1x2=(x1+x2)2+2x1x2=9-2=7.
新知探究
已知关于x的方程x2+(2k-1)x+k2-1=0有两个实数根x1,x2.
2
(1)关于x的方程x2+(2k-1)x+k2-1=0有两个实数根x1,x2,
Δ=(2k-1)2-4(k2-1)=-4k+5≥0,
(1)求实数k的取值范围;
(2)若x1,x2满足x12+x22=16+x1x2,求实数k的值.
解得k≤ ,实数k的取值范围为(-∞, ].
新知探究
已知关于x的方程x2+(2k-1)x+k2-1=0有两个实数根x1,x2.
2
(2)关于x的方程x2+(2k-1)x+k2-1=0有两个实数根x1,x2,x1+x2=1-2k,x1x2=k2-1.
(1)求实数k的取值范围;
(2)若x1,x2满足x12+x22=16+x1x2,求实数k的值.
∵x12+x22=(x1+x2)2-2x1x2=16+x1x2,
∴(1-2k)2-2(k2-1)=16+(k2-1),即k2-4k-12=0,
新知探究
已知关于x的方程x2+(2k-1)x+k2-1=0有两个实数根x1,x2.
2
解得k=-2或k=6(不符合题意,舍去).
(1)求实数k的取值范围;
(2)若x1,x2满足x12+x22=16+x1x2,求实数k的值.
所以实数k的值为-2.
归纳小结
回顾本节课,你有什么收获?
(1)一元二次方程根与系数的关系是什么?
(2)一元二次方程根与系数的关系使用条件是什么?
作业:教科书P51练习B 2、3.
作业布置
再见
第2课时
问题1 阅读课本第47~49页,回答下列问题:
整体概览
(1)本节将要研究一元二次方程的根与系数的关系.(2)起点是一元二次方程的解法及求根公式,目标是会求解一元二次方程的两根和与两根积,并灵活运用根与系数的关系解决问题.提升数学运算素养.
(1)本节将要研究哪类问题?
(2)本节要研究的问题在数学中的地位是怎样的?
情境与问题
学完一元二次方程的解集后,我就听到了咱班的小奕和小涵的一段悄悄话,内容如下:
小奕:小涵,我发现了一个秘密!
小涵:什么秘密?
小奕:你知道咱们尊敬的刘老师的年龄吗?
小涵:不知道哎!
情境与问题
小奕:呵呵,这绝对是个秘密,我不能直接告诉你,我这么说吧:她的年龄是一元二次方程x2-13x+36=0的两根的积,回去你把两根求出来就知道了.
小涵:咳,这你可难不住我,我不用求根就已经知道答案了,而且我还告诉你,刘老师的年龄是方程x2-36x-40=0的两根的和呢.
小奕:哈哈,你太有才了.对了,咱们应该也让同学们猜一猜,不解方程,能不能求出刘老师的年龄.
新知探究
问题 一元二次方程ax2+bx+c=0(a≠0)若有实数根,它的根是两个吗?这两根的和与积有什么特殊性吗?
前面我们已经知道,一元二次方程ax2+bx+c=0(a≠0)的解集情形:
(1)当Δ=b2-4ac>0时,方程的解集为
(2)当Δ=b2-4ac=0时,方程的解集为
新知探究
问题 一元二次方程ax2+bx+c=0(a≠0)若有实数根,它的根是两个吗?这两根的和与积有什么特殊性吗?
(3)当Δ=b2-4ac<0时,方程的解集为?.
当Δ=b2-4ac≥0时,方程ax2+bx+c=0(a≠0)有两个实数根(当Δ=0时,x1=x2,按照初中的习惯,我们仍称方程有两个相等的实数根),计算可得:这两个实数根的和与积分别为
新知探究
问题 一元二次方程ax2+bx+c=0(a≠0)若有实数根,它的根是两个吗?这两根的和与积有什么特殊性吗?
(1)用语言叙述为:一元二次方程的解集不空时,两根之和为一次项系数与二次项系数之比的相反数;两根之积为常数项与二次项系数之比.
(2)ax2+bx+c=0(a≠0)的两根是x1,x2,用式子表示为:x1+x2= ,x1x2= .这个结论通常称为一元二次方程根与系数的关系.
新知探究
【数学文化】法国数学家弗朗索瓦·韦达在著作《论方程的识别与订正》中建立了方程根与系数的关系,提出了这条定理.??由于韦达最早发现代数方程的根与系数之间有这种关系,人们把这个关系称为韦达定理.
新知探究
例1 已知一元二次方程2x2+3x-4=0的两根为x1与x2,求下列各式的值:
(1)x12+x22; (2)|x1-x2|.
问题:是否要求出x1和x2,并由此给出上述(1)和(2)的答案?
新知探究
由一元二次方程根与系数的关系,得x1+x2= ,x1x2=-2,
(1)由上有x12+x22=(x1+x2)2-2x1x2
=( )2-2×(-2)
(2)因为(x1-x2)2=(x1+x2)2-4x1x2
=( )2-4×(-2)
所以|x1-x2|= .
新知探究
例2 已知关于x的一元二次方程mx2-(m+2)x+ =0有两个不相等的实数根x1,x2.若 =4m,试求m的值.
由题知 ,
解得m>-1且m≠0.
因为x1+x2= ,x1x2= ,
所以 ,
解得m=2或m=-1.
又因为m>-1,所以m=2.
新知探究
例3 已知方程x2+tx+1=0,根据下列条件,分别求出t的取值范围.
(1)两个根都大于0;
(2)两个根都小于0;
设方程x2+tx+1=0的两个根为x1,x2.
所以t的取值范围为(-∞,-2].
(1)由题意得 ,解得t≤-2.
新知探究
例3 已知方程x2+tx+1=0,根据下列条件,分别求出t的取值范围.
(1)两个根都大于0;
(2)两个根都小于0;
设方程x2+tx+1=0的两个根为x1,x2.
所以t的取值范围为[2,+∞).
(2) ,解得t≥2.
新知探究
【想一想】是否存在t,使方程x2+tx+1=0一个根大于0,另一个根小于0.
由前面知道:若有解,两根积为1是正数,所以不可能两根异号的,即不存在实数t使得方程的一个根大于0,另一个根小于0.
新知探究
已知x1,x2是一元二次方程x2-3x-1=0的两个实数根,求x12+x22+4x1x2的值.
1
根据一元二次方程根与系数的关系可知x1+x2=3,x1x2=-1.
所以x12+x22+4x1x2=(x1+x2)2+2x1x2=9-2=7.
新知探究
已知关于x的方程x2+(2k-1)x+k2-1=0有两个实数根x1,x2.
2
(1)关于x的方程x2+(2k-1)x+k2-1=0有两个实数根x1,x2,
Δ=(2k-1)2-4(k2-1)=-4k+5≥0,
(1)求实数k的取值范围;
(2)若x1,x2满足x12+x22=16+x1x2,求实数k的值.
解得k≤ ,实数k的取值范围为(-∞, ].
新知探究
已知关于x的方程x2+(2k-1)x+k2-1=0有两个实数根x1,x2.
2
(2)关于x的方程x2+(2k-1)x+k2-1=0有两个实数根x1,x2,x1+x2=1-2k,x1x2=k2-1.
(1)求实数k的取值范围;
(2)若x1,x2满足x12+x22=16+x1x2,求实数k的值.
∵x12+x22=(x1+x2)2-2x1x2=16+x1x2,
∴(1-2k)2-2(k2-1)=16+(k2-1),即k2-4k-12=0,
新知探究
已知关于x的方程x2+(2k-1)x+k2-1=0有两个实数根x1,x2.
2
解得k=-2或k=6(不符合题意,舍去).
(1)求实数k的取值范围;
(2)若x1,x2满足x12+x22=16+x1x2,求实数k的值.
所以实数k的值为-2.
归纳小结
回顾本节课,你有什么收获?
(1)一元二次方程根与系数的关系是什么?
(2)一元二次方程根与系数的关系使用条件是什么?
作业:教科书P51练习B 2、3.
作业布置
再见
