3.3函数的应用(一) 课件24张PPT
文档属性
| 名称 | 3.3函数的应用(一) 课件24张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 225.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-02 00:00:00 | ||
图片预览








文档简介
函数的应用(一)
问题1 一次函数、反比例函数、二次函数、幂函数的解析式分别是什么?你能举例说明与此有关的生活实例吗?
问题导入
一次函数:f(x)=kx+b(k,b为常数,k≠0);
二次函数:f(x)=ax2+bx+c(a,b,c为常数,a≠0);
幂函数:f(x)=xα(α为常数);
生活实例略.
反比例函数:f(x)= (k为常数,k≠0);
例1 设小王的专项扣除比例、专项附加扣除金额、依法确定的其他扣除金额与3.1.2例8相同,全年综合所得收入额为x(单位:元),应缴纳综合所得个税税额为y(单位:元).
新知探究
(1)求y关于x的函数解析式;
(2)如果小王全年的综合所得由189600元增加到249600元,那么他全年应缴纳多少综合所得个税?
追问1 本题中涉及了几个变量?你能写出它们之间的关系吗?
本题涉及的变量:
全年综合所得收入额x,应纳税所得额t,应缴纳个税y,
由个人应纳税所得额计算公式,
可得t=x-60000-x(8%+2%+1%+9%)-52800-4560
令t≤0,得x≤146700;
=0.8x-117360.
令t>0,得x>146700.
所以个人应纳税所得额t=
新知探究
追问1 本题中涉及了几个变量?你能写出它们之间的关系吗?
由3.1.2例8可知个税税额
③
新知探究
追问2 如何通过这两个关系确定应缴纳个税税额y与综合所得收入额x之间的关系?
在③中,将t用关于x的关系式代换,并将t的范围换成自变量x的范围.
新知探究
追问3 当x在什么范围内时可以使t落到相应的区间?
当0≤x≤146700时,t=0;
要使0<t≤36000,只需0<0.8x-117360≤36000,
可得146700<x≤191700;
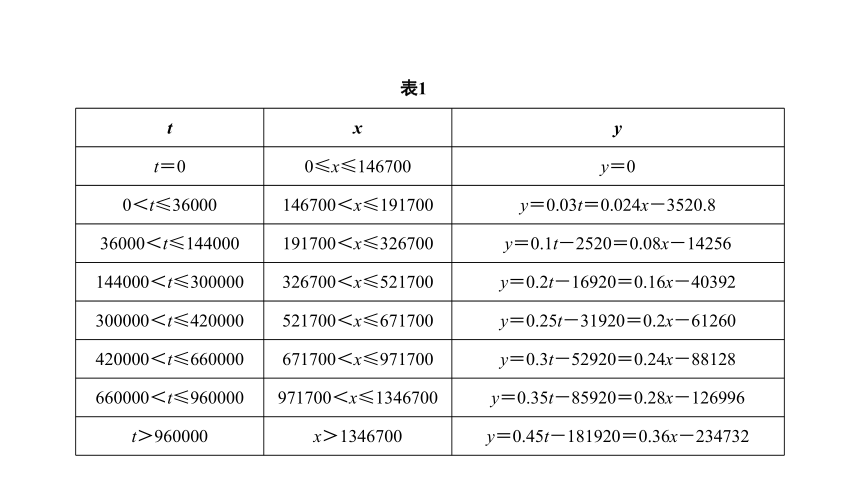
同理可得其它区间内的对应范围,答案见表1.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}t
x
y
t=0
0≤x≤146700
y=0
0<t≤36000
146700<x≤191700
y=0.03t=0.024x-3520.8
36000<t≤144000
191700<x≤326700
y=0.1t-2520=0.08x-14256
144000<t≤300000
326700<x≤521700
y=0.2t-16920=0.16x-40392
300000<t≤420000
521700<x≤671700
y=0.25t-31920=0.2x-61260
420000<t≤660000
671700<x≤971700
y=0.3t-52920=0.24x-88128
660000<t≤960000
971700<x≤1346700
y=0.35t-85920=0.28x-126996
t>960000
x>1346700
y=0.45t-181920=0.36x-234732
表1
新知探究
新知探究
例1 (1)求y关于x的函数解析式;
解:(1)函数解析式为
④
新知探究
例1 (2)如果小王全年的综合所得由189600元增加到249600元,那么他全年应缴纳多少综合所得个税?
解:(2)根据④,当x=249600时,y=0.08×249600-14256=5712.
所以,小王全年需要缴纳的综合所得个税税额为5712元.
追问4 对比这个例子和3.1.2例8,请谈谈你的感受.
3.1.2例8中,要由综合收入所得额求出应纳税所得额,才能计算个税税额,本例直接将个税表示成了综合收入所得的函数,由此可直接由综合收入所得额求出需要缴纳的个税税额.
网络上计算个税税额、房贷还款额的小程序都是先建立函数模型,再由程序员编写程序做成的.由此可见,有了函数模型,就可以通过研究函数获得实际问题的答案.
新知探究
例2 一辆汽车在某段路程中行驶的平均速率v(单位:km/h)与时间t(单位:h)的关系如图1所示,
(1)求图中阴影部分的面积,并说明所求面积的实际含义;
(2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004 km,试建立行驶这段路程时汽车里程表读数s (单位:km)与时间t的函数解析式,并画出相应的图象.
新知探究
图1
(1)求图中阴影部分的面积,并说明所求面积的实际含义;
解:阴影部分的面积为
50×1+80×1+90×1+75×1+65×1=360.
阴影部分的面积表示汽车在这5 h内行驶的路程为360 km.
新知探究
例2 一辆汽车在某段路程中行驶的平均速率v(单位:km/h)与时间t(单位:h)的关系如图1所示,
图1
追问1 任取区间[0,5]内的一个时刻t0,你能在图1中画出对应的路程吗?
?t0∈[0,5],t=t0这条直线左边的阴影面积就是经过t0时间的路程,如图2所示.
新知探究
图2
追问2 由追问1我们知道汽车行驶路程l是关于时间t的函数,你能写出它的函数解析式吗?
当0≤t<1时,l=50t;
当1≤t<2时,l=80(t-1)+50;
当2≤t<3时,l=90(t-2)+130;
当3≤t<4时,l=75(t-3)+220;
当4≤t≤5时,l=65(t-4)+295.
新知探究
解:设汽车行驶路程为l,
则
新知探究
例2 (2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004 km,试建立行驶这段路程时汽车里程表读数s (单位:km)与时间t的函数解析式,并画出相应的图象.
解:又因为s=l+2004,所以
这个函数的图象如图3所示.
新知探究
例2 (2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004 km,试建立行驶这段路程时汽车里程表读数s (单位:km)与时间t的函数解析式,并画出相应的图象.
图3
追问3 你能根据图3画出汽车行驶路程关于时间变化的图象吗?为什么?
实际上这个图象可以由图3的函数图象向下平移2004个单位得到.因为相同的自变量t对应的里程数s与路程l的差等于定值2004.
新知探究
问题2 回忆本节课的内容,请你回答以下几个问题:
归纳小结
(1)你能说说应用函数知识解决实际问题的一般步骤吗?
(2)你认为最关键的步骤是什么?
(1)①阅读理解,抓取信息,即确定实际问题中的变量;
②建立函数模型,即确定变量间的关系;
③求函数模型的解;
④作答,即把数学结果转译成具体问题的结论.
(2)建立函数模型,确定问题中函数的对应关系与定义域.
作业:教科书习题3.4第1,2,3,4,5题.
作业布置
1.若用模型描述汽车紧急刹车后滑行的距离y(单位:m)与刹车时的速率x(单位:km/h)的关系,而某种型号的汽车在速率为60 km/h时,紧急刹车后滑行的距离为20 m.在限速为100 km/h的高速公路上,一辆这种型号的车紧急刹车后滑行的距离为50 m,那么这辆车是否超速行驶?
目标检测
因为30<100,所以这辆车没有超车.
解:由20=(60)2a解得a= ,
由50= x2解得x= ,
1
2.某广告公司要为客户设计一幅周长为(单位:m)的矩形广告牌,如何设计这个广告牌可以使广告牌的面积最大?
目标检测
解:设矩形的一边长为x,广告牌面积为S,
则S=-(x- )2+ ,x∈(0, ).
当x= 时,S取到最大值,且Smax= .
所以当广告牌是边长为 的正方形时,广告牌的面积最大.
2
3.某公司生产某种产品的固定成本为150万元,而每件产品的可变成本为2500元,每件产品的售价为3500元.若该公司所生产的产品全部销售出去,则
(1)设总成本为y1(单位:万元),单位成本为y2(单位:万元),销售总收入为y3(单位:万元),总利润为y4(单位:万元),分别求出它们关于总产量x(单位:件)的函数解析式.
目标检测
(2)根据所求函数的图象,对这个公司的经济效益作出简单分析.
答案: (1)y1=150+0.25x;
y2=+0.25;
y3=0.35x;
y4=0.1x-150.
3
3.某公司生产某种产品的固定成本为150万元,而每件产品的可变成本为2500元,每件产品的售价为3500元.若该公司所生产的产品全部销售出去,则
(2)根据所求函数的图象,对这个公司的经济效益作出简单分析.
目标检测
答案: (2)当x<1500件时,该公司亏损;
当x=1500件时,公司不赔不赚;
当x>1500件时,公司盈利.
3
再见
问题1 一次函数、反比例函数、二次函数、幂函数的解析式分别是什么?你能举例说明与此有关的生活实例吗?
问题导入
一次函数:f(x)=kx+b(k,b为常数,k≠0);
二次函数:f(x)=ax2+bx+c(a,b,c为常数,a≠0);
幂函数:f(x)=xα(α为常数);
生活实例略.
反比例函数:f(x)= (k为常数,k≠0);
例1 设小王的专项扣除比例、专项附加扣除金额、依法确定的其他扣除金额与3.1.2例8相同,全年综合所得收入额为x(单位:元),应缴纳综合所得个税税额为y(单位:元).
新知探究
(1)求y关于x的函数解析式;
(2)如果小王全年的综合所得由189600元增加到249600元,那么他全年应缴纳多少综合所得个税?
追问1 本题中涉及了几个变量?你能写出它们之间的关系吗?
本题涉及的变量:
全年综合所得收入额x,应纳税所得额t,应缴纳个税y,
由个人应纳税所得额计算公式,
可得t=x-60000-x(8%+2%+1%+9%)-52800-4560
令t≤0,得x≤146700;
=0.8x-117360.
令t>0,得x>146700.
所以个人应纳税所得额t=
新知探究
追问1 本题中涉及了几个变量?你能写出它们之间的关系吗?
由3.1.2例8可知个税税额
③
新知探究
追问2 如何通过这两个关系确定应缴纳个税税额y与综合所得收入额x之间的关系?
在③中,将t用关于x的关系式代换,并将t的范围换成自变量x的范围.
新知探究
追问3 当x在什么范围内时可以使t落到相应的区间?
当0≤x≤146700时,t=0;
要使0<t≤36000,只需0<0.8x-117360≤36000,
可得146700<x≤191700;
同理可得其它区间内的对应范围,答案见表1.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}t
x
y
t=0
0≤x≤146700
y=0
0<t≤36000
146700<x≤191700
y=0.03t=0.024x-3520.8
36000<t≤144000
191700<x≤326700
y=0.1t-2520=0.08x-14256
144000<t≤300000
326700<x≤521700
y=0.2t-16920=0.16x-40392
300000<t≤420000
521700<x≤671700
y=0.25t-31920=0.2x-61260
420000<t≤660000
671700<x≤971700
y=0.3t-52920=0.24x-88128
660000<t≤960000
971700<x≤1346700
y=0.35t-85920=0.28x-126996
t>960000
x>1346700
y=0.45t-181920=0.36x-234732
表1
新知探究
新知探究
例1 (1)求y关于x的函数解析式;
解:(1)函数解析式为
④
新知探究
例1 (2)如果小王全年的综合所得由189600元增加到249600元,那么他全年应缴纳多少综合所得个税?
解:(2)根据④,当x=249600时,y=0.08×249600-14256=5712.
所以,小王全年需要缴纳的综合所得个税税额为5712元.
追问4 对比这个例子和3.1.2例8,请谈谈你的感受.
3.1.2例8中,要由综合收入所得额求出应纳税所得额,才能计算个税税额,本例直接将个税表示成了综合收入所得的函数,由此可直接由综合收入所得额求出需要缴纳的个税税额.
网络上计算个税税额、房贷还款额的小程序都是先建立函数模型,再由程序员编写程序做成的.由此可见,有了函数模型,就可以通过研究函数获得实际问题的答案.
新知探究
例2 一辆汽车在某段路程中行驶的平均速率v(单位:km/h)与时间t(单位:h)的关系如图1所示,
(1)求图中阴影部分的面积,并说明所求面积的实际含义;
(2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004 km,试建立行驶这段路程时汽车里程表读数s (单位:km)与时间t的函数解析式,并画出相应的图象.
新知探究
图1
(1)求图中阴影部分的面积,并说明所求面积的实际含义;
解:阴影部分的面积为
50×1+80×1+90×1+75×1+65×1=360.
阴影部分的面积表示汽车在这5 h内行驶的路程为360 km.
新知探究
例2 一辆汽车在某段路程中行驶的平均速率v(单位:km/h)与时间t(单位:h)的关系如图1所示,
图1
追问1 任取区间[0,5]内的一个时刻t0,你能在图1中画出对应的路程吗?
?t0∈[0,5],t=t0这条直线左边的阴影面积就是经过t0时间的路程,如图2所示.
新知探究
图2
追问2 由追问1我们知道汽车行驶路程l是关于时间t的函数,你能写出它的函数解析式吗?
当0≤t<1时,l=50t;
当1≤t<2时,l=80(t-1)+50;
当2≤t<3时,l=90(t-2)+130;
当3≤t<4时,l=75(t-3)+220;
当4≤t≤5时,l=65(t-4)+295.
新知探究
解:设汽车行驶路程为l,
则
新知探究
例2 (2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004 km,试建立行驶这段路程时汽车里程表读数s (单位:km)与时间t的函数解析式,并画出相应的图象.
解:又因为s=l+2004,所以
这个函数的图象如图3所示.
新知探究
例2 (2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004 km,试建立行驶这段路程时汽车里程表读数s (单位:km)与时间t的函数解析式,并画出相应的图象.
图3
追问3 你能根据图3画出汽车行驶路程关于时间变化的图象吗?为什么?
实际上这个图象可以由图3的函数图象向下平移2004个单位得到.因为相同的自变量t对应的里程数s与路程l的差等于定值2004.
新知探究
问题2 回忆本节课的内容,请你回答以下几个问题:
归纳小结
(1)你能说说应用函数知识解决实际问题的一般步骤吗?
(2)你认为最关键的步骤是什么?
(1)①阅读理解,抓取信息,即确定实际问题中的变量;
②建立函数模型,即确定变量间的关系;
③求函数模型的解;
④作答,即把数学结果转译成具体问题的结论.
(2)建立函数模型,确定问题中函数的对应关系与定义域.
作业:教科书习题3.4第1,2,3,4,5题.
作业布置
1.若用模型描述汽车紧急刹车后滑行的距离y(单位:m)与刹车时的速率x(单位:km/h)的关系,而某种型号的汽车在速率为60 km/h时,紧急刹车后滑行的距离为20 m.在限速为100 km/h的高速公路上,一辆这种型号的车紧急刹车后滑行的距离为50 m,那么这辆车是否超速行驶?
目标检测
因为30<100,所以这辆车没有超车.
解:由20=(60)2a解得a= ,
由50= x2解得x= ,
1
2.某广告公司要为客户设计一幅周长为(单位:m)的矩形广告牌,如何设计这个广告牌可以使广告牌的面积最大?
目标检测
解:设矩形的一边长为x,广告牌面积为S,
则S=-(x- )2+ ,x∈(0, ).
当x= 时,S取到最大值,且Smax= .
所以当广告牌是边长为 的正方形时,广告牌的面积最大.
2
3.某公司生产某种产品的固定成本为150万元,而每件产品的可变成本为2500元,每件产品的售价为3500元.若该公司所生产的产品全部销售出去,则
(1)设总成本为y1(单位:万元),单位成本为y2(单位:万元),销售总收入为y3(单位:万元),总利润为y4(单位:万元),分别求出它们关于总产量x(单位:件)的函数解析式.
目标检测
(2)根据所求函数的图象,对这个公司的经济效益作出简单分析.
答案: (1)y1=150+0.25x;
y2=+0.25;
y3=0.35x;
y4=0.1x-150.
3
3.某公司生产某种产品的固定成本为150万元,而每件产品的可变成本为2500元,每件产品的售价为3500元.若该公司所生产的产品全部销售出去,则
(2)根据所求函数的图象,对这个公司的经济效益作出简单分析.
目标检测
答案: (2)当x<1500件时,该公司亏损;
当x=1500件时,公司不赔不赚;
当x>1500件时,公司盈利.
3
再见
