3.1.2《函数的单调性》 课件1(16张PPT)
文档属性
| 名称 | 3.1.2《函数的单调性》 课件1(16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 162.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-02 00:00:00 | ||
图片预览


文档简介
函数的单调性
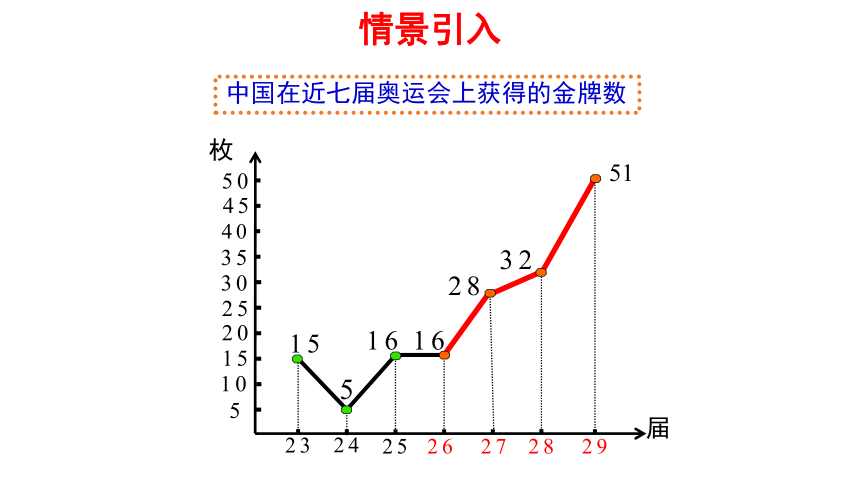
情景引入
中国在近七届奥运会上获得的金牌数
届
枚
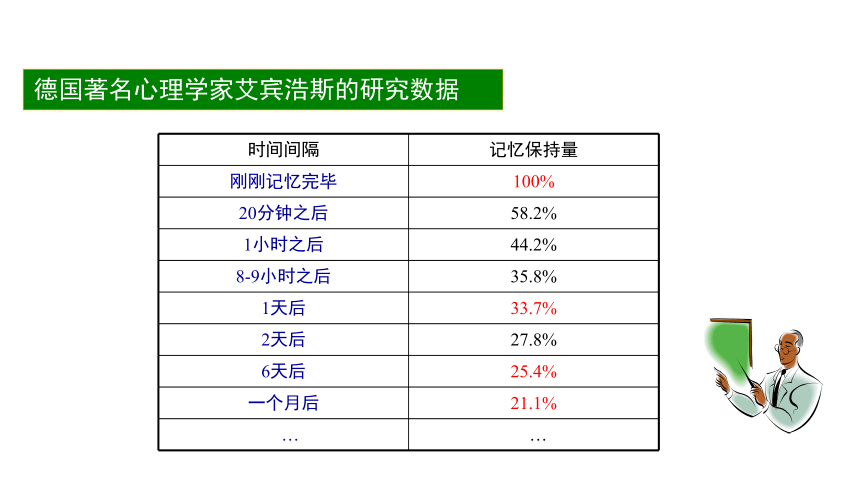
德国著名心理学家艾宾浩斯的研究数据
时间间隔
记忆保持量
刚刚记忆完毕
100%
20分钟之后
58.2%
1小时之后
44.2%
8-9小时之后
35.8%
1天后
33.7%
2天后
27.8%
6天后
25.4%
一个月后
21.1%
…
…
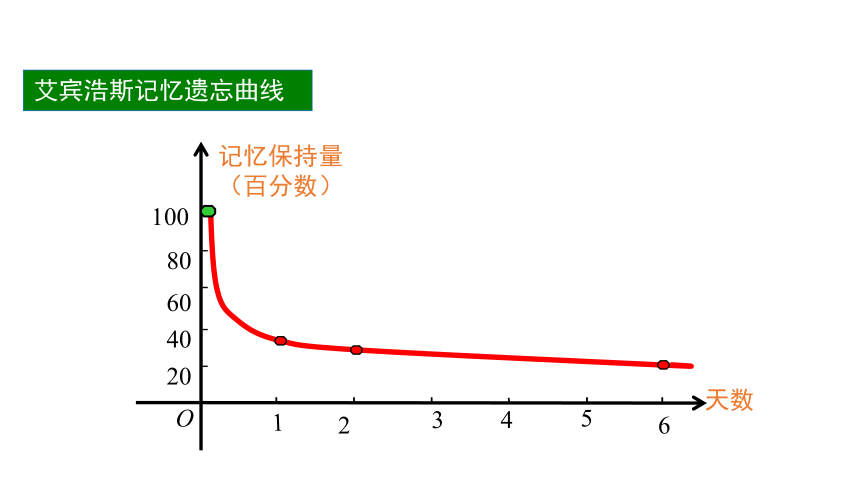
情景引入
艾宾浩斯记忆遗忘曲线
记忆保持量(百分数)
天数
O
20
40
60
80
100
3
2
1
4
5
6
情景引入
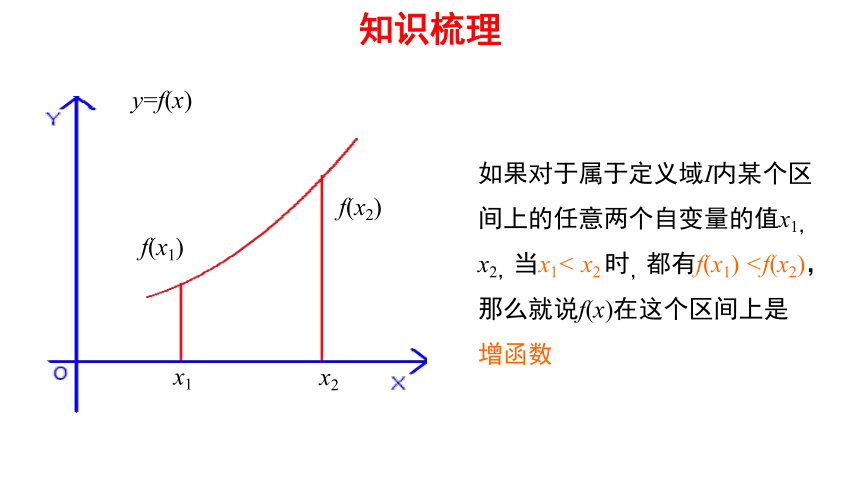
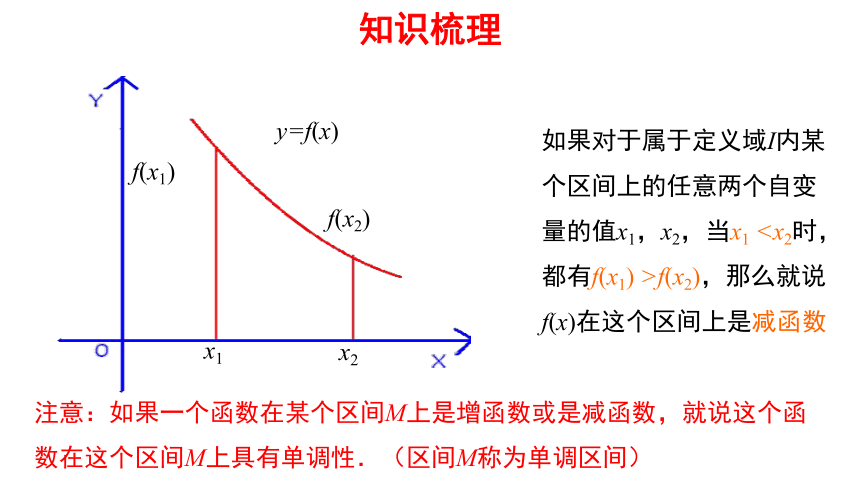
知识梳理
x1
x2
y=f(x)
f(x1)
f(x2)
如果对于属于定义域I内某个区间上的任意两个自变量的值x1,x2,当x1< x2 时,都有f(x1)y=f(x)
f(x1)
f(x2)
x1
x2
如果对于属于定义域I内某个区间上的任意两个自变量的值x1,x2,当x1f(x2),那么就说f(x)在这个区间上是减函数
注意:如果一个函数在某个区间M上是增函数或是减函数,就说这个函数在这个区间M上具有单调性.(区间M称为单调区间)
知识梳理
1.证明函数f(x)=2x+1在(-∞,+∞)上是增函数.
例题巩固
证明:设x1,x2是任意两个不相等的实数,且x1<x2
则:
所以函数f(x)=2x+1在(-∞,+∞)上是增函数
2.证明函数 ,在区间(-∞,0)和(0,+∞)上分别是减函数.
证明:设x1,x2是(-∞,0)内的任意两个不相等的负实数,且x1<x2,
则:
例题巩固
2.证明函数 ,在区间(-∞,0)和(0,+∞)上分别是减函数.
同理,对区间( 0,+∞ )内的任意两个不相等的正实数x1,x2 ,且x1<x2 ,同样有
例题巩固
练习精讲
1.下图是定义在闭区间[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一个单调区间上,y=f(x)是增函数还是减函数.
y=f(x)
解:函数y=f(x) 的单调区间有[-5,-2),[-2,1),[1,3),[3,5],其中y=f(x)在区间[-5,-2), [1,3)上是减函数,在区间[-2,1), [3,5]上是增函数.
练习精讲
2.证明函数f(x) =3x+2 在R上是增函数
证明:设x1,x2是R上的任意两个实数,且x1 < x2,则
f(x1) -f(x2) =(3x1+2)-(3x2+2)
=3(x1-x2)
由x1 < x2,得x1 - x2 < 0,
于是 f(x1) -f(x2) < 0,
即 f(x1) < f(x2)
所以,f(x) =3x+2 在R上是增函数
练习精讲
课堂小结
1.函数的单调性
一般地,设函数f(x)的定义域为 I :
如果对于属于定义域 I 内某个区间上的任意两个自变量的值x1 , x2,当x1<x2时,都有f(x1)<f(x2),那么就说f(x)在这个区间上是增函数.如果对于属于定义域I内某个区间上的任意两个自变量的值x1,x2,当x1<x2时,都有f(x1)>f(x2),那么就说f(x)在这个区间上是减函数.函数是增函数还是减函数.是对定义域内某个区间而言的.有的函数在一些区间上是增函数,而在另一些区间上可能是减函数,例如函数y=x2,当x∈[0,+∞]时是增函数,当x∈(-∞,0)时是减函数.
2.单调区间
如果函数y=f(x)在某个区间是增函数或减函数,那么就说函数y=f(x)在这一区间上具有(严格的)单调性,这一区间叫做y=f(x)的单调区间.在单调区间上增函数的图象是上升的,减函数的图象是下降的.
课堂小结
3.用定义证明函数单调性的步骤
证明函数f(x)在区间M上具有单调性的步骤:
(1)取值:对任意x1,x2∈M,且x1<x2;
(2)作差:f(x1)-f(x2);
(3)判定差的正负;
(4)根据判定的结果作出相应的结论.
课堂小结
谢谢观看
情景引入
中国在近七届奥运会上获得的金牌数
届
枚
德国著名心理学家艾宾浩斯的研究数据
时间间隔
记忆保持量
刚刚记忆完毕
100%
20分钟之后
58.2%
1小时之后
44.2%
8-9小时之后
35.8%
1天后
33.7%
2天后
27.8%
6天后
25.4%
一个月后
21.1%
…
…
情景引入
艾宾浩斯记忆遗忘曲线
记忆保持量(百分数)
天数
O
20
40
60
80
100
3
2
1
4
5
6
情景引入
知识梳理
x1
x2
y=f(x)
f(x1)
f(x2)
如果对于属于定义域I内某个区间上的任意两个自变量的值x1,x2,当x1< x2 时,都有f(x1)
f(x1)
f(x2)
x1
x2
如果对于属于定义域I内某个区间上的任意两个自变量的值x1,x2,当x1
注意:如果一个函数在某个区间M上是增函数或是减函数,就说这个函数在这个区间M上具有单调性.(区间M称为单调区间)
知识梳理
1.证明函数f(x)=2x+1在(-∞,+∞)上是增函数.
例题巩固
证明:设x1,x2是任意两个不相等的实数,且x1<x2
则:
所以函数f(x)=2x+1在(-∞,+∞)上是增函数
2.证明函数 ,在区间(-∞,0)和(0,+∞)上分别是减函数.
证明:设x1,x2是(-∞,0)内的任意两个不相等的负实数,且x1<x2,
则:
例题巩固
2.证明函数 ,在区间(-∞,0)和(0,+∞)上分别是减函数.
同理,对区间( 0,+∞ )内的任意两个不相等的正实数x1,x2 ,且x1<x2 ,同样有
例题巩固
练习精讲
1.下图是定义在闭区间[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一个单调区间上,y=f(x)是增函数还是减函数.
y=f(x)
解:函数y=f(x) 的单调区间有[-5,-2),[-2,1),[1,3),[3,5],其中y=f(x)在区间[-5,-2), [1,3)上是减函数,在区间[-2,1), [3,5]上是增函数.
练习精讲
2.证明函数f(x) =3x+2 在R上是增函数
证明:设x1,x2是R上的任意两个实数,且x1 < x2,则
f(x1) -f(x2) =(3x1+2)-(3x2+2)
=3(x1-x2)
由x1 < x2,得x1 - x2 < 0,
于是 f(x1) -f(x2) < 0,
即 f(x1) < f(x2)
所以,f(x) =3x+2 在R上是增函数
练习精讲
课堂小结
1.函数的单调性
一般地,设函数f(x)的定义域为 I :
如果对于属于定义域 I 内某个区间上的任意两个自变量的值x1 , x2,当x1<x2时,都有f(x1)<f(x2),那么就说f(x)在这个区间上是增函数.如果对于属于定义域I内某个区间上的任意两个自变量的值x1,x2,当x1<x2时,都有f(x1)>f(x2),那么就说f(x)在这个区间上是减函数.函数是增函数还是减函数.是对定义域内某个区间而言的.有的函数在一些区间上是增函数,而在另一些区间上可能是减函数,例如函数y=x2,当x∈[0,+∞]时是增函数,当x∈(-∞,0)时是减函数.
2.单调区间
如果函数y=f(x)在某个区间是增函数或减函数,那么就说函数y=f(x)在这一区间上具有(严格的)单调性,这一区间叫做y=f(x)的单调区间.在单调区间上增函数的图象是上升的,减函数的图象是下降的.
课堂小结
3.用定义证明函数单调性的步骤
证明函数f(x)在区间M上具有单调性的步骤:
(1)取值:对任意x1,x2∈M,且x1<x2;
(2)作差:f(x1)-f(x2);
(3)判定差的正负;
(4)根据判定的结果作出相应的结论.
课堂小结
谢谢观看
