沪科版八年级数学上册(第11_12章)综合测试试题(word版,含答案)
文档属性
| 名称 | 沪科版八年级数学上册(第11_12章)综合测试试题(word版,含答案) | 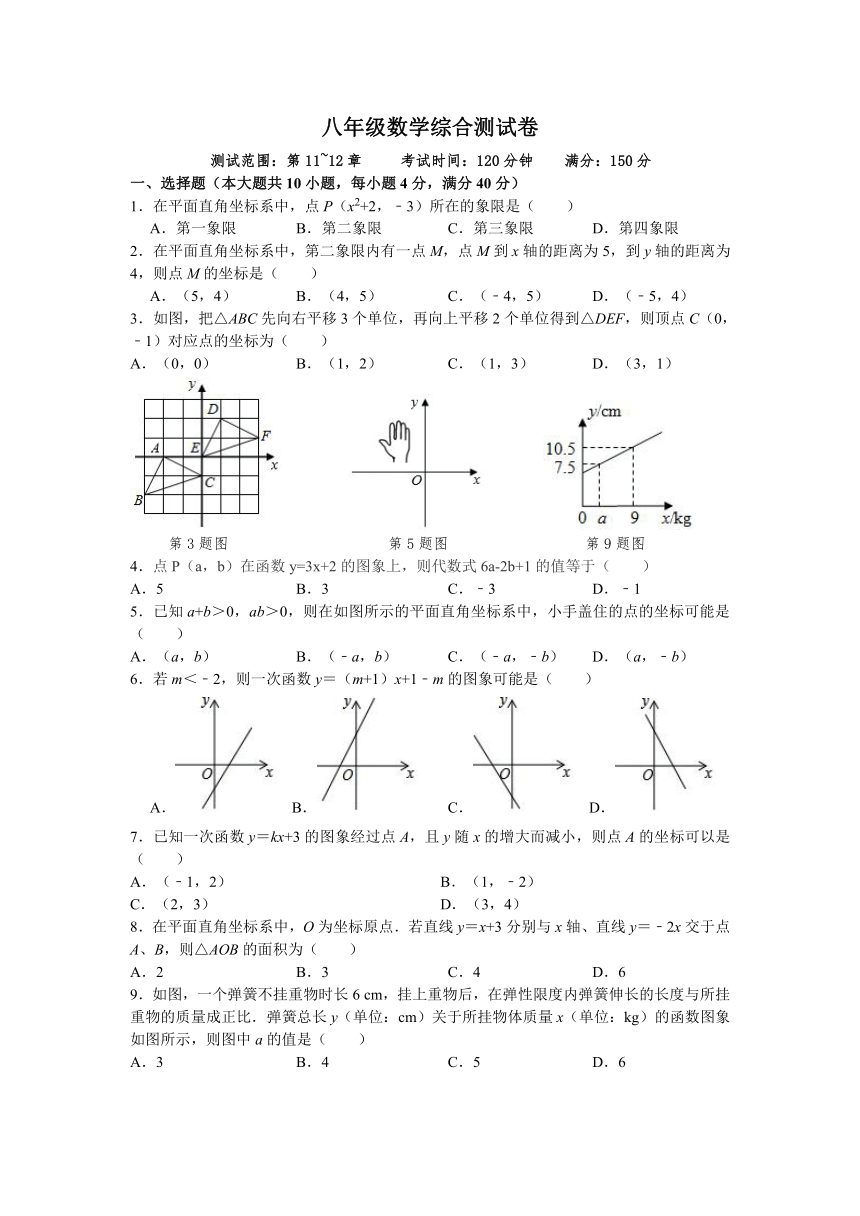 | |
| 格式 | doc | ||
| 文件大小 | 133.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-02 05:45:04 | ||
图片预览




文档简介
八年级数学综合测试卷
测试范围:第11~12章 考试时间:120分钟 满分:150分
一、选择题(本大题共10小题,每小题4分,满分40分)
1.在平面直角坐标系中,点P(x2+2,﹣3)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.在平面直角坐标系中,第二象限内有一点M,点M到x轴的距离为5,到y轴的距离为4,则点M的坐标是( )
A.(5,4) B.(4,5) C.(﹣4,5) D.(﹣5,4)
3.如图,把△ABC先向右平移3个单位,再向上平移2个单位得到△DEF,则顶点C(0,﹣1)对应点的坐标为( )
A.(0,0) B.(1,2) C.(1,3) D.(3,1)
第3题图 第5题图 第9题图
4.点P(a,b)在函数y=3x+2的图象上,则代数式6a-2b+1的值等于( )
A.5 B.3 C.﹣3 D.﹣1
5.已知a+b>0,ab>0,则在如图所示的平面直角坐标系中,小手盖住的点的坐标可能是( )
A.(a,b) B.(﹣a,b) C.(﹣a,﹣b) D.(a,﹣b)
6.若m<﹣2,则一次函数y=(m+1)x+1﹣m的图象可能是( )
A. B. C. D.
7.已知一次函数y=kx+3的图象经过点A,且y随x的增大而减小,则点A的坐标可以是( )
A.(﹣1,2) B.(1,﹣2)
C.(2,3) D.(3,4)
8.在平面直角坐标系中,O为坐标原点.若直线y=x+3分别与x轴、直线y=﹣2x交于点A、B,则△AOB的面积为( )
A.2 B.3 C.4 D.6
9.如图,一个弹簧不挂重物时长6 cm,挂上重物后,在弹性限度内弹簧伸长的长度与所挂重物的质量成正比.弹簧总长y(单位:cm)关于所挂物体质量x(单位:kg)的函数图象如图所示,则图中a的值是( )
A.3 B.4 C.5 D.6
10.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),……按这样的运动规律,经过第2021次运动后,动点P的坐标是( )
A.(2021,0) B.(2020,1) C.(2021,1) D.(2021,2)
第10题图 第14题图
二、填空题(本大题共4小题,每小题5分,满分20分)
11.点P(m,2)在第二象限内,则m的值可以是(写出一个即可) .
12.在函数y=中,自变量x的取值范围是 .
13.点(﹣,m)和点(2,n)在直线y=2x+b上,则m与n的大小关系是 .
14.某企业用货车向乡镇运送农用物资,行驶2小时后,天空突然下起大雨,影响车辆行驶速度,货车行驶的路程y(km)与行驶时间x(h)的函数关系如图所示,2小时后货车的速度是 km/h.
三、(本大题共2小题,每小题8分,满分16分)
15.已知一次函数y=kx+b,它的图象经过(1,﹣3),(4,6)两点.
(1)求y与x之间的函数关系式;
(2)若点(a,3)在这个函数图象上,求a的值.
16.已知点P(2m+4,m﹣1),试分别根据下列条件,求出P点的坐标.
(1)点P在y轴上;
(2)点P在过点A(2,3)且与x轴平行的直线上.
四、(本大题共2小题,每小题8分,满分16分)
17.已知一次函数y=kx+b的图象经过点(﹣2,5),并且与y轴相交于点P,直线y=
﹣x+3与y轴相交于点Q,点Q恰与点P关于x轴对称,求这个一次函数y=kx+b的表达式.
18.在平面直角坐标系中,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的勾股值,记为:「P」,即「P」=|x|+|y|.
(1)求点A(﹣1,3)的勾股值「A」;
(2)若点B在第一象限且满足「B」=3,求满足条件的所有B点与坐标轴围成的图形的面积.
五、(本大题共2小题,每小题10分,满分20分)
19.为迎接新年,某单位组织员工开展娱乐竞赛活动,工会计划购进A、B两种电器共21件作为奖品.已知A种电器每件90元,B种电器每件70元.设购买B种电器x件,购买两种电器所需费用为y元.
(1)y关于x的函数关系式为: ;
(2)若购买B种电器的数量少于A种电器的数量,请给出一种最省费用的方案,并求出该方案所需费用.
20.如图,已知直线l1:y1=﹣2x﹣3,直线l2:y2=x+3,l1与l2相交于点P,l1,l2分别与y轴相交于点A,B.
(1)求点P的坐标;
(2)若y1>y2>0,求x的取值范围;
(3)点D(m,0)为x轴上的一个动点,过点D作x轴的垂线分别交l1和l2于点E,F,当EF=3时,求m的值.
六、(本题满分12分)
21.如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.
(1)写出A′、B′、C′的坐标;
(2)求出△ABC的面积;
(3)点P在y轴上,且△BCP与△ABC的面积相等,求点P的坐标.
七、(本题满分12分)
22.合肥享有“中国淡水龙虾之都”的美称,甲、乙两家小龙虾美食店,平时以同样的价格出售品质相同的小龙虾.“龙虾节”期间,甲、乙两家店都让利酬宾,在人数不超过20人的前提下,付款金额y甲、y乙(单位:元)与人数之间的函数关系如图所示.
(1)直接写出y甲,y乙关于x的函数关系式;
(2)小王公司想在“龙虾节”期间组织团建,在甲、乙两家店就餐,如何选择甲、乙两家美食店吃小龙虾更省钱?
八、(本题满分14分)
23.在平面直角坐标系xOy中,△ABC如图所示,点A(﹣3,2),B(1,1),C(0,4).
(1)求直线AB的解析式;
(2)求△ABC的面积;
(3)已知一次函数y=ax+3a+2(a为常数).
①求证:一次函数y=ax+3a+2的图象一定经过点A;
②若一次函数y=ax+3a+2的图象与线段BC有交点,直接写出a的取值范围.
答 案
1.D 2.C 3.D 4.C 5.B 6.D 7.B 8.B 9.A
10.C 解析:观察点的坐标变化可知:第1次从原点运动到点(1,1),
第2次接着运动到点(2,0),第3次接着运动到点(3,2),
第4次接着运动到点(4,0),第5次接着运动到点(5,1),
…按这样的运动规律,
发现每个点的横坐标与次数相等,
纵坐标是1,0,2,0,4每个数一个循环,
因为2021÷4=505……1,所以经过第2021次运动后,
动点P的坐标是(2021,1).故选C.
11.﹣1(答案不唯一) 12.x>0.5 13.m<n
14.65 解析:当x≥2时,设函数解析式为y=kx+b,把(2,156)和(3,221)代入解析式,可得,解得,所以函数解析式为y=65x+26(x≥2),所以2小时后货车的速度是65km/h,或利用图象法,平均速度==65(km/h).故答案为65.
15.解:(1)将(1,﹣3),(4,6)代入y=kx+b中,得,解得,
∴y与x之间的函数关系式为y=3x﹣6.(4分)
(2)把点(a,3)代入y=3x﹣6中,得3a﹣6=3,解得a=3,∴a的值为3.(8分)
16.解:(1)令2m+4=0,解得m=﹣2,所以P点的坐标为(0,﹣3).(4分)
(2)由题意得点P的纵坐标与点A的纵坐标相等,令m﹣1=3,解得m=4.所以P点的坐标为(12,3).(8分)
17.解:由题意可得,点Q的坐标是(0,3),则点P的坐标是(0,﹣3),
把(0,﹣3),(﹣2,5)代入一次函数y=kx+b得解得
所以这个一次函数的表达式为y=﹣4x﹣3.(8分)
18.解:(1)「A」=|﹣1|+|3|=4.(3分)
(2)设B(x,y),由「B」=3且点B在第一象限知,x+y=3(x>0,y>0),
即:y=﹣x+3(x>0,y>0).故所有点B与坐标轴围成的图形为如图所示的三角形,
故其面积为×3×3=.(8分)
19.解:(1)y=﹣20x+1890(4分)
(2)∵y=﹣20x+1890,﹣20<0,∴y随x的增大而减小,∴x取最大值时,y最小.
∵购买B种电器的数量少于A种电器的数量,∴x<21﹣x,∴x<10.5.
∵x为整数,∴x的最大值为10,∴当x=10时,y有最小值,为1690,21﹣x=11.
∴使费用最省的方案是购买B种电器10件,A种电器11件,所需费用为1690元.(10分)
20.解:(1)根据题意,得,解得,
∴点P的坐标为(﹣2,1).(3分)
(2)在直线l2:y2=x+3中,令y=0,解得x=﹣3.
由图象可知:若y1>y2>0,x的取值范围是﹣3<x<﹣2.(6分)
(3)由题意可知E(m,﹣2m﹣3),F(m,m+3).
∵EF=3,∴|﹣2m﹣3﹣m﹣3|=3,解得m=﹣3或m=﹣1.(10分)
21.解:(1)如图所示,A′(0,4)、B′(﹣1,1)、C′(3,1).(3分)
(2)S△ABC=×(3+1)×3=6.(7分)
(3)设点P坐标为(0,y),∵BC=4,点P到BC的距离为|y+2|,由题意得×4×|y+2|=6,解得y=1或y=﹣5,∴点P的坐标为(0,1)或(0,﹣5).(12分)
22.解:(1)y甲=25x+200,.(6分)
(2)当0≤x≤10时,令25x+200=60x,解得x=.
当10<x≤20时,令25x+200=600,解得x=16.
答:当人数不超过5人时,小王公司应该选择在乙店吃小龙虾更省钱;当人数超过5人且小于16人时,小王公司应该选择在甲店吃小龙虾更省钱;当人数为16人时到两个店的总费用相同;当人数超过16人且不超过20人时,小王公司应该选择在乙店吃小龙虾更省钱.(12分)
23.解:(1)设直线AB的解析式是y=kx+b,将点A(﹣3,2),点B(1,1)代入,得,解得,∴直线AB的解析式是.(4分)
(2)设直线AB与y轴的交点为D点,则点D的坐标为,
.(8分)
(3)①证明:∵y=ax+3a+2=a(x+3)+2,∴y=ax+3a+2必过点(﹣3,2),即必过A点;
②把B(1,1)代入y=ax+3a+2得,1=a+3a+2,解得a=﹣;
把C(0,4)代入y=ax+3a+2得,4=3a+2,解得a=,
∴若一次函数y=ax+3a+2的图象与线段BC有交点,则且a≠0.(14分)
测试范围:第11~12章 考试时间:120分钟 满分:150分
一、选择题(本大题共10小题,每小题4分,满分40分)
1.在平面直角坐标系中,点P(x2+2,﹣3)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.在平面直角坐标系中,第二象限内有一点M,点M到x轴的距离为5,到y轴的距离为4,则点M的坐标是( )
A.(5,4) B.(4,5) C.(﹣4,5) D.(﹣5,4)
3.如图,把△ABC先向右平移3个单位,再向上平移2个单位得到△DEF,则顶点C(0,﹣1)对应点的坐标为( )
A.(0,0) B.(1,2) C.(1,3) D.(3,1)
第3题图 第5题图 第9题图
4.点P(a,b)在函数y=3x+2的图象上,则代数式6a-2b+1的值等于( )
A.5 B.3 C.﹣3 D.﹣1
5.已知a+b>0,ab>0,则在如图所示的平面直角坐标系中,小手盖住的点的坐标可能是( )
A.(a,b) B.(﹣a,b) C.(﹣a,﹣b) D.(a,﹣b)
6.若m<﹣2,则一次函数y=(m+1)x+1﹣m的图象可能是( )
A. B. C. D.
7.已知一次函数y=kx+3的图象经过点A,且y随x的增大而减小,则点A的坐标可以是( )
A.(﹣1,2) B.(1,﹣2)
C.(2,3) D.(3,4)
8.在平面直角坐标系中,O为坐标原点.若直线y=x+3分别与x轴、直线y=﹣2x交于点A、B,则△AOB的面积为( )
A.2 B.3 C.4 D.6
9.如图,一个弹簧不挂重物时长6 cm,挂上重物后,在弹性限度内弹簧伸长的长度与所挂重物的质量成正比.弹簧总长y(单位:cm)关于所挂物体质量x(单位:kg)的函数图象如图所示,则图中a的值是( )
A.3 B.4 C.5 D.6
10.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),……按这样的运动规律,经过第2021次运动后,动点P的坐标是( )
A.(2021,0) B.(2020,1) C.(2021,1) D.(2021,2)
第10题图 第14题图
二、填空题(本大题共4小题,每小题5分,满分20分)
11.点P(m,2)在第二象限内,则m的值可以是(写出一个即可) .
12.在函数y=中,自变量x的取值范围是 .
13.点(﹣,m)和点(2,n)在直线y=2x+b上,则m与n的大小关系是 .
14.某企业用货车向乡镇运送农用物资,行驶2小时后,天空突然下起大雨,影响车辆行驶速度,货车行驶的路程y(km)与行驶时间x(h)的函数关系如图所示,2小时后货车的速度是 km/h.
三、(本大题共2小题,每小题8分,满分16分)
15.已知一次函数y=kx+b,它的图象经过(1,﹣3),(4,6)两点.
(1)求y与x之间的函数关系式;
(2)若点(a,3)在这个函数图象上,求a的值.
16.已知点P(2m+4,m﹣1),试分别根据下列条件,求出P点的坐标.
(1)点P在y轴上;
(2)点P在过点A(2,3)且与x轴平行的直线上.
四、(本大题共2小题,每小题8分,满分16分)
17.已知一次函数y=kx+b的图象经过点(﹣2,5),并且与y轴相交于点P,直线y=
﹣x+3与y轴相交于点Q,点Q恰与点P关于x轴对称,求这个一次函数y=kx+b的表达式.
18.在平面直角坐标系中,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的勾股值,记为:「P」,即「P」=|x|+|y|.
(1)求点A(﹣1,3)的勾股值「A」;
(2)若点B在第一象限且满足「B」=3,求满足条件的所有B点与坐标轴围成的图形的面积.
五、(本大题共2小题,每小题10分,满分20分)
19.为迎接新年,某单位组织员工开展娱乐竞赛活动,工会计划购进A、B两种电器共21件作为奖品.已知A种电器每件90元,B种电器每件70元.设购买B种电器x件,购买两种电器所需费用为y元.
(1)y关于x的函数关系式为: ;
(2)若购买B种电器的数量少于A种电器的数量,请给出一种最省费用的方案,并求出该方案所需费用.
20.如图,已知直线l1:y1=﹣2x﹣3,直线l2:y2=x+3,l1与l2相交于点P,l1,l2分别与y轴相交于点A,B.
(1)求点P的坐标;
(2)若y1>y2>0,求x的取值范围;
(3)点D(m,0)为x轴上的一个动点,过点D作x轴的垂线分别交l1和l2于点E,F,当EF=3时,求m的值.
六、(本题满分12分)
21.如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.
(1)写出A′、B′、C′的坐标;
(2)求出△ABC的面积;
(3)点P在y轴上,且△BCP与△ABC的面积相等,求点P的坐标.
七、(本题满分12分)
22.合肥享有“中国淡水龙虾之都”的美称,甲、乙两家小龙虾美食店,平时以同样的价格出售品质相同的小龙虾.“龙虾节”期间,甲、乙两家店都让利酬宾,在人数不超过20人的前提下,付款金额y甲、y乙(单位:元)与人数之间的函数关系如图所示.
(1)直接写出y甲,y乙关于x的函数关系式;
(2)小王公司想在“龙虾节”期间组织团建,在甲、乙两家店就餐,如何选择甲、乙两家美食店吃小龙虾更省钱?
八、(本题满分14分)
23.在平面直角坐标系xOy中,△ABC如图所示,点A(﹣3,2),B(1,1),C(0,4).
(1)求直线AB的解析式;
(2)求△ABC的面积;
(3)已知一次函数y=ax+3a+2(a为常数).
①求证:一次函数y=ax+3a+2的图象一定经过点A;
②若一次函数y=ax+3a+2的图象与线段BC有交点,直接写出a的取值范围.
答 案
1.D 2.C 3.D 4.C 5.B 6.D 7.B 8.B 9.A
10.C 解析:观察点的坐标变化可知:第1次从原点运动到点(1,1),
第2次接着运动到点(2,0),第3次接着运动到点(3,2),
第4次接着运动到点(4,0),第5次接着运动到点(5,1),
…按这样的运动规律,
发现每个点的横坐标与次数相等,
纵坐标是1,0,2,0,4每个数一个循环,
因为2021÷4=505……1,所以经过第2021次运动后,
动点P的坐标是(2021,1).故选C.
11.﹣1(答案不唯一) 12.x>0.5 13.m<n
14.65 解析:当x≥2时,设函数解析式为y=kx+b,把(2,156)和(3,221)代入解析式,可得,解得,所以函数解析式为y=65x+26(x≥2),所以2小时后货车的速度是65km/h,或利用图象法,平均速度==65(km/h).故答案为65.
15.解:(1)将(1,﹣3),(4,6)代入y=kx+b中,得,解得,
∴y与x之间的函数关系式为y=3x﹣6.(4分)
(2)把点(a,3)代入y=3x﹣6中,得3a﹣6=3,解得a=3,∴a的值为3.(8分)
16.解:(1)令2m+4=0,解得m=﹣2,所以P点的坐标为(0,﹣3).(4分)
(2)由题意得点P的纵坐标与点A的纵坐标相等,令m﹣1=3,解得m=4.所以P点的坐标为(12,3).(8分)
17.解:由题意可得,点Q的坐标是(0,3),则点P的坐标是(0,﹣3),
把(0,﹣3),(﹣2,5)代入一次函数y=kx+b得解得
所以这个一次函数的表达式为y=﹣4x﹣3.(8分)
18.解:(1)「A」=|﹣1|+|3|=4.(3分)
(2)设B(x,y),由「B」=3且点B在第一象限知,x+y=3(x>0,y>0),
即:y=﹣x+3(x>0,y>0).故所有点B与坐标轴围成的图形为如图所示的三角形,
故其面积为×3×3=.(8分)
19.解:(1)y=﹣20x+1890(4分)
(2)∵y=﹣20x+1890,﹣20<0,∴y随x的增大而减小,∴x取最大值时,y最小.
∵购买B种电器的数量少于A种电器的数量,∴x<21﹣x,∴x<10.5.
∵x为整数,∴x的最大值为10,∴当x=10时,y有最小值,为1690,21﹣x=11.
∴使费用最省的方案是购买B种电器10件,A种电器11件,所需费用为1690元.(10分)
20.解:(1)根据题意,得,解得,
∴点P的坐标为(﹣2,1).(3分)
(2)在直线l2:y2=x+3中,令y=0,解得x=﹣3.
由图象可知:若y1>y2>0,x的取值范围是﹣3<x<﹣2.(6分)
(3)由题意可知E(m,﹣2m﹣3),F(m,m+3).
∵EF=3,∴|﹣2m﹣3﹣m﹣3|=3,解得m=﹣3或m=﹣1.(10分)
21.解:(1)如图所示,A′(0,4)、B′(﹣1,1)、C′(3,1).(3分)
(2)S△ABC=×(3+1)×3=6.(7分)
(3)设点P坐标为(0,y),∵BC=4,点P到BC的距离为|y+2|,由题意得×4×|y+2|=6,解得y=1或y=﹣5,∴点P的坐标为(0,1)或(0,﹣5).(12分)
22.解:(1)y甲=25x+200,.(6分)
(2)当0≤x≤10时,令25x+200=60x,解得x=.
当10<x≤20时,令25x+200=600,解得x=16.
答:当人数不超过5人时,小王公司应该选择在乙店吃小龙虾更省钱;当人数超过5人且小于16人时,小王公司应该选择在甲店吃小龙虾更省钱;当人数为16人时到两个店的总费用相同;当人数超过16人且不超过20人时,小王公司应该选择在乙店吃小龙虾更省钱.(12分)
23.解:(1)设直线AB的解析式是y=kx+b,将点A(﹣3,2),点B(1,1)代入,得,解得,∴直线AB的解析式是.(4分)
(2)设直线AB与y轴的交点为D点,则点D的坐标为,
.(8分)
(3)①证明:∵y=ax+3a+2=a(x+3)+2,∴y=ax+3a+2必过点(﹣3,2),即必过A点;
②把B(1,1)代入y=ax+3a+2得,1=a+3a+2,解得a=﹣;
把C(0,4)代入y=ax+3a+2得,4=3a+2,解得a=,
∴若一次函数y=ax+3a+2的图象与线段BC有交点,则且a≠0.(14分)
