人教版九年级数学上册 24.1.2 垂直于弦的直径 同步练习卷(Word版 含答案)
文档属性
| 名称 | 人教版九年级数学上册 24.1.2 垂直于弦的直径 同步练习卷(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 256.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-02 13:11:16 | ||
图片预览

文档简介
24.1.2 垂直于弦的直径
一.选择题
1.如图,⊙O中,OD⊥AB于点C,OB=13,AB=24,则OC的长为( )
A.3 B.4 C.5 D.6
2.某市某居民区一处圆形下水管道破裂,修理人员准备更换一段新管道.如图所示,污水水面宽度为60cm,水面至管道顶差距离为10cm,修理人员应准备内径为( )cm的管道.
A.50 B.50 C.100 D.80
3.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4cm,则球的半径长是( )
A.2 cm B.2.5 cm C.3 cm D.4 cm
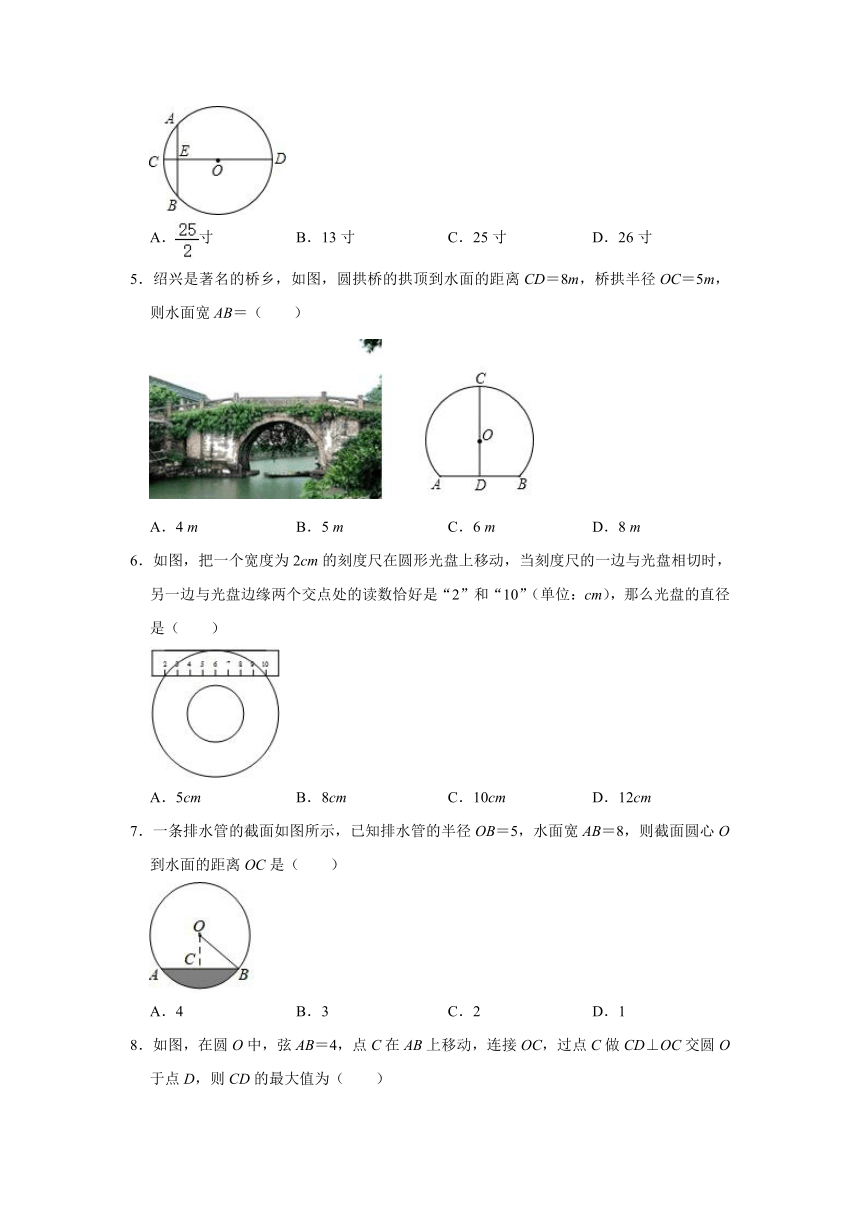
4.“圆材埋壁”是我国古代《九章算术》中的一个问题,“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代的数学语言表示是:“如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=10寸,求直径CD的长”.依题意,CD长为( )
A.寸 B.13寸 C.25寸 D.26寸
5.绍兴是著名的桥乡,如图,圆拱桥的拱顶到水面的距离CD=8m,桥拱半径OC=5m,则水面宽AB=( )
A.4 m B.5 m C.6 m D.8 m
6.如图,把一个宽度为2cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:cm),那么光盘的直径是( )
A.5cm B.8cm C.10cm D.12cm
7.一条排水管的截面如图所示,已知排水管的半径OB=5,水面宽AB=8,则截面圆心O到水面的距离OC是( )
A.4 B.3 C.2 D.1
8.如图,在圆O中,弦AB=4,点C在AB上移动,连接OC,过点C做CD⊥OC交圆O于点D,则CD的最大值为( )
A.2 B.2 C. D.
9.为了测量一个铁球的直径,将该铁球放入工件槽内,测得的有关数据如图所示(单位:cm),则该铁球的直径为( )
A.12cm B.10cm C.8cm D.6cm
10.往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,则水的最大深度为( )
A.8cm B.10cm C.16cm D.20cm
二.填空题
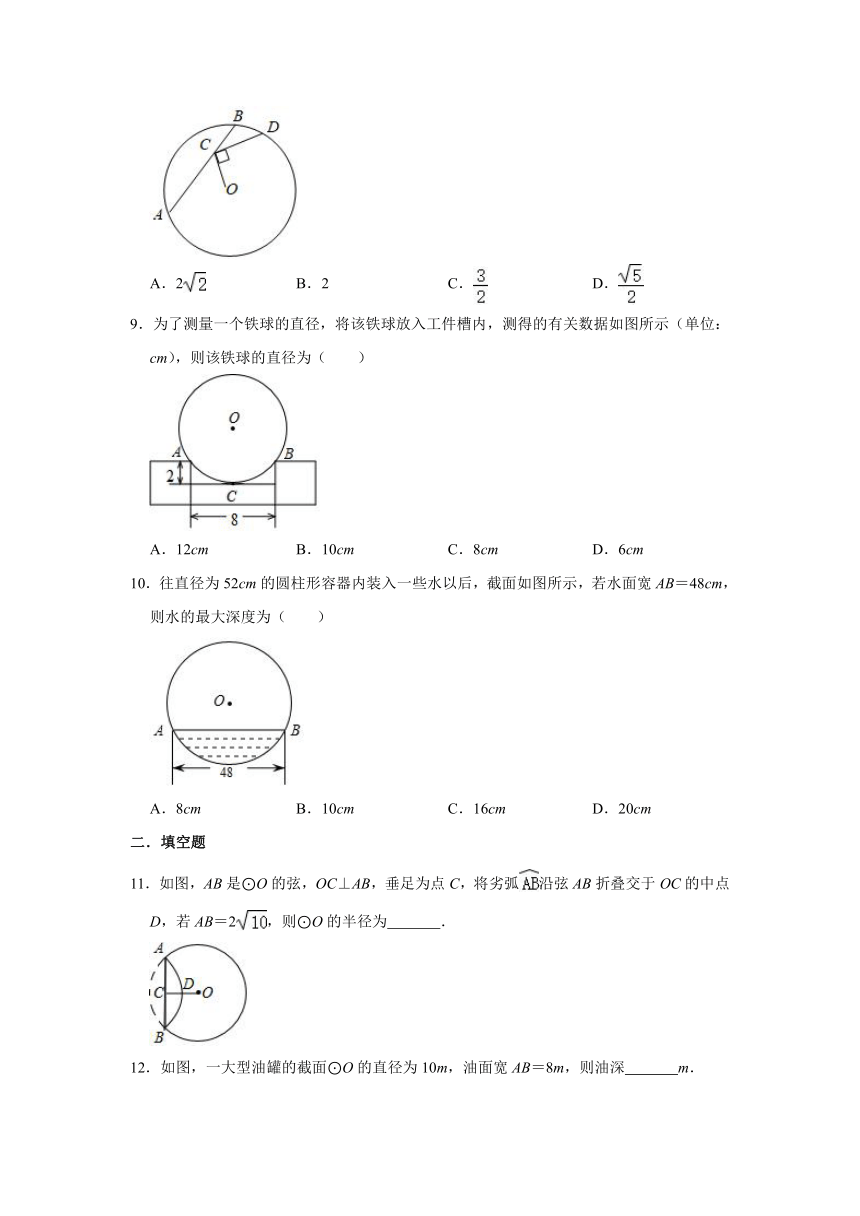
11.如图,AB是⊙O的弦,OC⊥AB,垂足为点C,将劣弧沿弦AB折叠交于OC的中点D,若AB=2,则⊙O的半径为 .
12.如图,一大型油罐的截面⊙O的直径为10m,油面宽AB=8m,则油深 m.
13.如图,在半径为10cm的圆形铁片上切下一块高为4cm的弓形铁片,则弓形弦AB的长为 .
14.如图,是一个隧道的横断面的示意图,它的形状是以点O为圆心的圆的一部分,如果
M是⊙O弦CD的中点,EM经过圆心O交圆O于点E,并且CD=4,EM=6,则⊙O的半径为 .
15.王江泾是著名的水乡,如图,圆拱桥的拱顶到水面的距离CD为9m,水面宽AB为6m,则桥拱半径OC为 m.
三.解答题
16.如图,点A,D,B,C在⊙O上,AB⊥BC,DE⊥AB于点E.若BC=3,AE=DE=1,求⊙O半径的长.
17.如图,在△OAB中OA=OB,⊙O交AB于点C、D,求证:AC=BD.
18.如图是输水管的切面,阴影部分是有水部分,其中水面AB宽10cm,水最深3cm,求输水管的半径.
19.某居民小区的一处圆柱形的输水管道破裂,维修人员为更换管道,需要确定管道圆形截面的半径.如图,若这个输水管道有水部分的水面宽AB=16cm,水最深的地方的高度为4cm,求这个圆形截面的半径.
参考答案
一.选择题
1. C.
2. C.
3. B.
4. D.
5. D.
6. C.
7. B.
8. B.
9. B.
10. C.
二.填空题
11. 3.
12. 8.
13. 16cm.
14. .
15. 5.
三.解答题
16.解:如图,连接AD,AC,连接CD与AB交于点F,
∵AB⊥BC,
∴∠ABC=90°.
∴AC为直径.
∴∠ADC=90°.
∵AE=DE,DE⊥AB,
∴∠DAB=∠ADE=45°.
∴∠BCF=∠DAB=45°.
∴BC=BF=3.
在△ADF中,∠DAB=∠AFD=45°,
∴EF=ED=1.
∴AB=5.
∴AC==.
∴⊙O半径的长.
17.证明:过点O作OE⊥AB于点E,
∵在⊙O中,OE⊥CD,
∴CE=DE,
∵OA=OB,OE⊥AB,
∴AE=BE,
∴AE﹣CE=BE﹣DE,
∴AC=BD.
18.解:设圆形切面的半径为r,过点O作OD⊥AB于点D,交⊙O于点E,
则AD=BD=AB=×10=5cm,
∵最深地方的高度是3cm,
∴OD=r﹣3,
在Rt△OBD中,
OB2=BD2+OD2,即r2=52+(r﹣3)2,
解得r=(cm),
∴输水管的半径为cm.
19.解:过点O作OC⊥AB于D,交⊙O于C,连接OB,
∵OC⊥AB
∴BD=AB=×16=8cm
由题意可知,CD=4cm
∴设半径为xcm,则OD=(x﹣4)cm
在Rt△BOD中,
由勾股定理得:OD2+BD2=OB2
(x﹣4)2+82=x2
解得:x=10.
答:这个圆形截面的半径为10cm.
一.选择题
1.如图,⊙O中,OD⊥AB于点C,OB=13,AB=24,则OC的长为( )
A.3 B.4 C.5 D.6
2.某市某居民区一处圆形下水管道破裂,修理人员准备更换一段新管道.如图所示,污水水面宽度为60cm,水面至管道顶差距离为10cm,修理人员应准备内径为( )cm的管道.
A.50 B.50 C.100 D.80
3.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4cm,则球的半径长是( )
A.2 cm B.2.5 cm C.3 cm D.4 cm
4.“圆材埋壁”是我国古代《九章算术》中的一个问题,“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代的数学语言表示是:“如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=10寸,求直径CD的长”.依题意,CD长为( )
A.寸 B.13寸 C.25寸 D.26寸
5.绍兴是著名的桥乡,如图,圆拱桥的拱顶到水面的距离CD=8m,桥拱半径OC=5m,则水面宽AB=( )
A.4 m B.5 m C.6 m D.8 m
6.如图,把一个宽度为2cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:cm),那么光盘的直径是( )
A.5cm B.8cm C.10cm D.12cm
7.一条排水管的截面如图所示,已知排水管的半径OB=5,水面宽AB=8,则截面圆心O到水面的距离OC是( )
A.4 B.3 C.2 D.1
8.如图,在圆O中,弦AB=4,点C在AB上移动,连接OC,过点C做CD⊥OC交圆O于点D,则CD的最大值为( )
A.2 B.2 C. D.
9.为了测量一个铁球的直径,将该铁球放入工件槽内,测得的有关数据如图所示(单位:cm),则该铁球的直径为( )
A.12cm B.10cm C.8cm D.6cm
10.往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,则水的最大深度为( )
A.8cm B.10cm C.16cm D.20cm
二.填空题
11.如图,AB是⊙O的弦,OC⊥AB,垂足为点C,将劣弧沿弦AB折叠交于OC的中点D,若AB=2,则⊙O的半径为 .
12.如图,一大型油罐的截面⊙O的直径为10m,油面宽AB=8m,则油深 m.
13.如图,在半径为10cm的圆形铁片上切下一块高为4cm的弓形铁片,则弓形弦AB的长为 .
14.如图,是一个隧道的横断面的示意图,它的形状是以点O为圆心的圆的一部分,如果
M是⊙O弦CD的中点,EM经过圆心O交圆O于点E,并且CD=4,EM=6,则⊙O的半径为 .
15.王江泾是著名的水乡,如图,圆拱桥的拱顶到水面的距离CD为9m,水面宽AB为6m,则桥拱半径OC为 m.
三.解答题
16.如图,点A,D,B,C在⊙O上,AB⊥BC,DE⊥AB于点E.若BC=3,AE=DE=1,求⊙O半径的长.
17.如图,在△OAB中OA=OB,⊙O交AB于点C、D,求证:AC=BD.
18.如图是输水管的切面,阴影部分是有水部分,其中水面AB宽10cm,水最深3cm,求输水管的半径.
19.某居民小区的一处圆柱形的输水管道破裂,维修人员为更换管道,需要确定管道圆形截面的半径.如图,若这个输水管道有水部分的水面宽AB=16cm,水最深的地方的高度为4cm,求这个圆形截面的半径.
参考答案
一.选择题
1. C.
2. C.
3. B.
4. D.
5. D.
6. C.
7. B.
8. B.
9. B.
10. C.
二.填空题
11. 3.
12. 8.
13. 16cm.
14. .
15. 5.
三.解答题
16.解:如图,连接AD,AC,连接CD与AB交于点F,
∵AB⊥BC,
∴∠ABC=90°.
∴AC为直径.
∴∠ADC=90°.
∵AE=DE,DE⊥AB,
∴∠DAB=∠ADE=45°.
∴∠BCF=∠DAB=45°.
∴BC=BF=3.
在△ADF中,∠DAB=∠AFD=45°,
∴EF=ED=1.
∴AB=5.
∴AC==.
∴⊙O半径的长.
17.证明:过点O作OE⊥AB于点E,
∵在⊙O中,OE⊥CD,
∴CE=DE,
∵OA=OB,OE⊥AB,
∴AE=BE,
∴AE﹣CE=BE﹣DE,
∴AC=BD.
18.解:设圆形切面的半径为r,过点O作OD⊥AB于点D,交⊙O于点E,
则AD=BD=AB=×10=5cm,
∵最深地方的高度是3cm,
∴OD=r﹣3,
在Rt△OBD中,
OB2=BD2+OD2,即r2=52+(r﹣3)2,
解得r=(cm),
∴输水管的半径为cm.
19.解:过点O作OC⊥AB于D,交⊙O于C,连接OB,
∵OC⊥AB
∴BD=AB=×16=8cm
由题意可知,CD=4cm
∴设半径为xcm,则OD=(x﹣4)cm
在Rt△BOD中,
由勾股定理得:OD2+BD2=OB2
(x﹣4)2+82=x2
解得:x=10.
答:这个圆形截面的半径为10cm.
同课章节目录
