22.2.1 配方法解一元二次方程--
文档属性
| 名称 | 22.2.1 配方法解一元二次方程-- |

|
|
| 格式 | zip | ||
| 文件大小 | 280.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-09-20 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
*
*
学习目标
1、理解掌握一元二次方程的四种解法;
2、了解什么是配方法?
3、会用配方法解一元二次方程。
*
开心练一练:
(1)
(2)
2、下列方程能用直接开平方法来解吗
创设情境 温故探新
1、用直接开平方法解下列方程:
静心想一想:
(1)
(2)
把两题转化成(x+b)2=a(a≥0)的
形式,再利用开平方
X2+6X+9 = 2
*
(1)
(2)
(3)
=( + )2
=( )2
=( )2
左边:所填常数等于一次项系数一半的平方.
填上适当的数或式,使下列各等式成立.
大胆试一试:
共同点:
( )2
=( )2
(4)
观察(1)(2)看所填的常数与一次项系数之间有什么关系
*
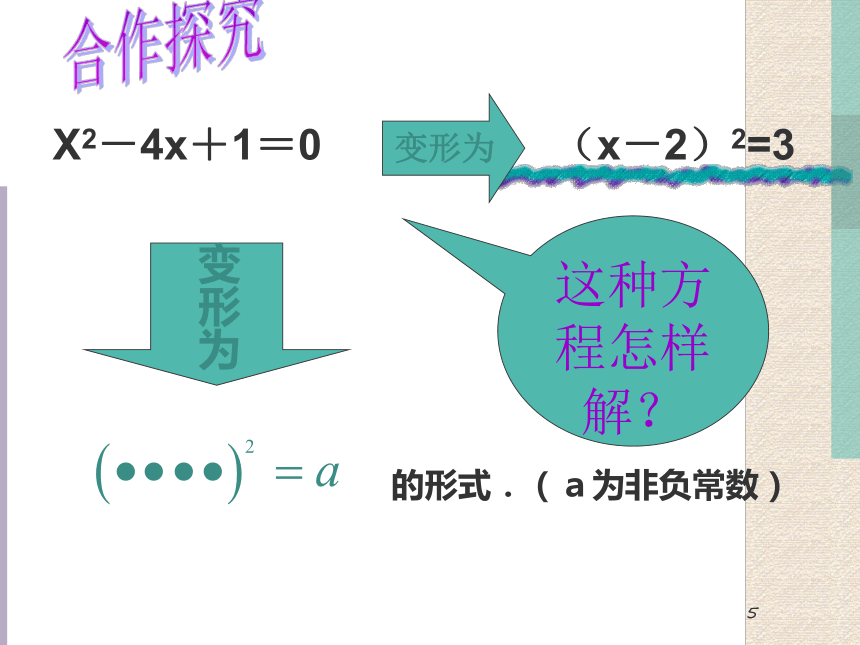
这种方程怎样解?
变形为
的形式.(a为非负常数)
变形为
X2-4x+1=0
(x-2)2=3
*
把一元二次方程左边是一个含有未知数的完全平方式,右边是一个非负常数,,然后用开平方法求解,这种解一元二次方程的方法叫做配方法.
(1)x2+8x+ =(x+4)2
(2)x2-4x+ =(x- )2
(3)x2-___x+ 9 =(x- )2
配方时, 等式两边同时加上的是一次项系数一半的平方。
16
6
3
4
2
*
。
填空:
25
36
5
6
*
问题: 要使一块矩形场地的长比宽多6m,并且面积为16m2, 场地的长和宽应各是多少?
(1)解:设场地宽为X米,则长为(x+6)米,根据题意得:
整理得:X2+6X-16 = 0
合作交流探究新知
X(X+6) = 16
*
移项
两边加上32,使左边配成
左边写成完全平方形式
降次
*
例题1. 用配方法解下列方程 x2+6x-7=0
解:移项,得
两边同时加上“一次项 系数一半的平方”,得
利用开平方法,得
所以,原方程的根是
*
例2. 用配方法解下列方程 2x2+8x-5=0
解:移项并且两边同除以2,得
两边同时加上“一次项 系数一半的平方”,得
利用开平方法,得
所以,原方程的根是
*
用配方法解一元二次方程的步骤:
1.化1:把二次项系数化为1;
2.移项:把常数项移到方程的右边;
3.配方:方程两边都加上一次项系数一半的平方;
4.开方:根据平方根意义,方程两边开平方;
5.求解:解一元一次方程;
6.定解:写出原方程的解.
*
练习:用配方法解下列方程
二次项系数为1
二次项系数不为1
可以先将系数化为1
*
1.方程x2+6x-5=0的左边配成完全平方后所得方程为( ).
(A)(x+3)2=14 (B) (x-3)2=14
(C) (x+6)2=14 (D)以上答案都不对
2.用配方法解下列方程,配方有错的是( )
(A)x2-2x-99=0 化为 (x-1)2=100
(B) 2x2-3x-2=0 化为 (x- 3/4 )2=25/16
(C)x2+8x+9=0 化为 (x+4)2=25
(D) 3x2-4x=2 化为(x-2/3)2=10/9
A
C
*
3.若实数x、y满足(x+y+2)(x+y-1)=0,
则x+y的值为( ).
(A)1 (B)-2
(C)2或-1 (D)-2或1
4.对于任意的实数x,代数式x2-5x+10的值是一个( )
(A)非负数 (B)正数
(C)整数 (D)不能确定的数
D
B
*
5.用配方法解下列方程:
(1)x2+6x=1
(2)x2=6-5x
(3) -x2+4x-3=0
(4) x2+12x =-9
注意:解第(2)题时要先移项,变形成x2+5x=6的形式;
如果方程的二次项系数为负,则先把二次项系数化为正.
6. 用配方法说明:不论k取何实数,多项式
k2-3k+5的值必定大于零.
X1=-1,x2=-11
*
1、已知
求
的值。
的二次三项式
是一个完全平方式,
的值。
3、已知关于
求实数
4.将边长为5的正方形边长增加x,所得正方形的面积比 原来正方形面积大15,求x的值
*
5.先用配方法解下列方程:
(1) x2-2x-1=0 (2) x2-2x+4=0
(3) x2-2x+1=0
然后回答下列问题:
(1)你在求解过程中遇到什么问题?你是怎样处理所遇到的问题的?
(2)对于形如x2+px+q=0这样的方程,在什么条件下才有实数根?
*
1.把一元二次方程的左边配成一个完全平方式,然后用开平方法求解,这种解一元二次方程的方法叫做配方法.
1.二次项系数化为1;
2.移项:把常数项移到方程的右边;
3.配方:方程两边都加上一次项系数一半的平方;
4.开方:根据平方根意义,方程两边开平方;
5.求解:解一元一次方程;
6.定解:写出原方程的解.
2.用配方法解一元二次方程的步骤:
*
*
学习目标
1、理解掌握一元二次方程的四种解法;
2、了解什么是配方法?
3、会用配方法解一元二次方程。
*
开心练一练:
(1)
(2)
2、下列方程能用直接开平方法来解吗
创设情境 温故探新
1、用直接开平方法解下列方程:
静心想一想:
(1)
(2)
把两题转化成(x+b)2=a(a≥0)的
形式,再利用开平方
X2+6X+9 = 2
*
(1)
(2)
(3)
=( + )2
=( )2
=( )2
左边:所填常数等于一次项系数一半的平方.
填上适当的数或式,使下列各等式成立.
大胆试一试:
共同点:
( )2
=( )2
(4)
观察(1)(2)看所填的常数与一次项系数之间有什么关系
*
这种方程怎样解?
变形为
的形式.(a为非负常数)
变形为
X2-4x+1=0
(x-2)2=3
*
把一元二次方程左边是一个含有未知数的完全平方式,右边是一个非负常数,,然后用开平方法求解,这种解一元二次方程的方法叫做配方法.
(1)x2+8x+ =(x+4)2
(2)x2-4x+ =(x- )2
(3)x2-___x+ 9 =(x- )2
配方时, 等式两边同时加上的是一次项系数一半的平方。
16
6
3
4
2
*
。
填空:
25
36
5
6
*
问题: 要使一块矩形场地的长比宽多6m,并且面积为16m2, 场地的长和宽应各是多少?
(1)解:设场地宽为X米,则长为(x+6)米,根据题意得:
整理得:X2+6X-16 = 0
合作交流探究新知
X(X+6) = 16
*
移项
两边加上32,使左边配成
左边写成完全平方形式
降次
*
例题1. 用配方法解下列方程 x2+6x-7=0
解:移项,得
两边同时加上“一次项 系数一半的平方”,得
利用开平方法,得
所以,原方程的根是
*
例2. 用配方法解下列方程 2x2+8x-5=0
解:移项并且两边同除以2,得
两边同时加上“一次项 系数一半的平方”,得
利用开平方法,得
所以,原方程的根是
*
用配方法解一元二次方程的步骤:
1.化1:把二次项系数化为1;
2.移项:把常数项移到方程的右边;
3.配方:方程两边都加上一次项系数一半的平方;
4.开方:根据平方根意义,方程两边开平方;
5.求解:解一元一次方程;
6.定解:写出原方程的解.
*
练习:用配方法解下列方程
二次项系数为1
二次项系数不为1
可以先将系数化为1
*
1.方程x2+6x-5=0的左边配成完全平方后所得方程为( ).
(A)(x+3)2=14 (B) (x-3)2=14
(C) (x+6)2=14 (D)以上答案都不对
2.用配方法解下列方程,配方有错的是( )
(A)x2-2x-99=0 化为 (x-1)2=100
(B) 2x2-3x-2=0 化为 (x- 3/4 )2=25/16
(C)x2+8x+9=0 化为 (x+4)2=25
(D) 3x2-4x=2 化为(x-2/3)2=10/9
A
C
*
3.若实数x、y满足(x+y+2)(x+y-1)=0,
则x+y的值为( ).
(A)1 (B)-2
(C)2或-1 (D)-2或1
4.对于任意的实数x,代数式x2-5x+10的值是一个( )
(A)非负数 (B)正数
(C)整数 (D)不能确定的数
D
B
*
5.用配方法解下列方程:
(1)x2+6x=1
(2)x2=6-5x
(3) -x2+4x-3=0
(4) x2+12x =-9
注意:解第(2)题时要先移项,变形成x2+5x=6的形式;
如果方程的二次项系数为负,则先把二次项系数化为正.
6. 用配方法说明:不论k取何实数,多项式
k2-3k+5的值必定大于零.
X1=-1,x2=-11
*
1、已知
求
的值。
的二次三项式
是一个完全平方式,
的值。
3、已知关于
求实数
4.将边长为5的正方形边长增加x,所得正方形的面积比 原来正方形面积大15,求x的值
*
5.先用配方法解下列方程:
(1) x2-2x-1=0 (2) x2-2x+4=0
(3) x2-2x+1=0
然后回答下列问题:
(1)你在求解过程中遇到什么问题?你是怎样处理所遇到的问题的?
(2)对于形如x2+px+q=0这样的方程,在什么条件下才有实数根?
*
1.把一元二次方程的左边配成一个完全平方式,然后用开平方法求解,这种解一元二次方程的方法叫做配方法.
1.二次项系数化为1;
2.移项:把常数项移到方程的右边;
3.配方:方程两边都加上一次项系数一半的平方;
4.开方:根据平方根意义,方程两边开平方;
5.求解:解一元一次方程;
6.定解:写出原方程的解.
2.用配方法解一元二次方程的步骤:
同课章节目录
