人教版八年级数学上册课堂练习 第十五章 15.2 分式的运算 第四课时(Word版 含答案)
文档属性
| 名称 | 人教版八年级数学上册课堂练习 第十五章 15.2 分式的运算 第四课时(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 25.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-02 00:00:00 | ||
图片预览




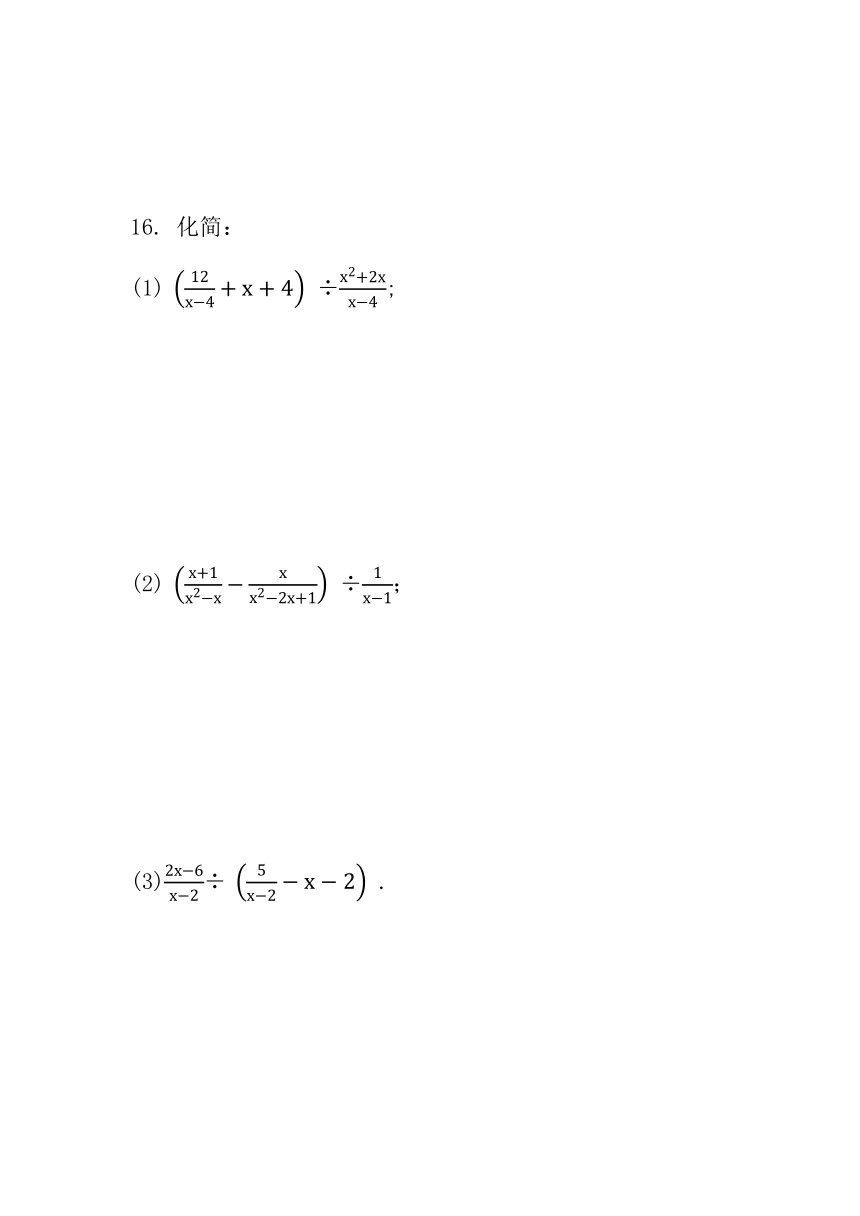
文档简介
课时训练
计算(x-1)÷
·x的结果是(
)
A.-x2
B.-1
C.x2
D.1
化简÷
的结果是(
)
A.x-4
B.x+3
C.
D.
化简
÷
的结果为(
)
A.
B.
C.
D.
若代数式
·的化简结果为2a-4,则整式A为(
)
A.a+1
B.a-1
C.-a-1
D.-a+1
如果2a-1=0,那么代数式
·的值是(
)
A.
B.
C.
D.3
小王上山速度为a
km/h,下山原路返回,速度为b
km/h,则小王上下山的平均速度为(
)
A.
km/h
B.
km/h
C.
km/h
D.
km/h
化简:
·=
.
如果a-b=2,那么代数式
·的值为
.
若a2-6a+9与
互为相反数,则
÷(a+b)=
.
已知x+y=4,x-y=,则式子
的值是
.
对于正数x,规定
f(x)=,例如:f(4)==,f
==,则f(2
019)+f(2
018)+…+f(2)+f(1)+f
+…+f
+f
=
.
计算:
(1)÷
=
;
(2)÷
=
.
化简:
(1)
÷;
(2)1+÷
.
先化简,再求值:
÷,其中x=3+.
先化简,再求值:
÷,其中a为不等式组的整数解.
化简:
(1)
÷;
(2)
÷;
(3)÷
.
先化简,再求值:
(1)
÷
,其中a是方程a2-4a+2=0的解.
(2)
÷,其中x=2.
(3)
÷
,其中a=.
(4)化简式子
÷,并在-2,-1,0,1,2中选取一个合适的数作为a的值代入求值.
甲、乙两工程队分别承担一条2千米的公路维修工作,甲队有一半时间每天维修公路x千米,另一半时间每天维修公路y千米.乙队维修前1千米时,每天维修公路x千米,乙队维修后1千米时,每天维修公路y千米(x≠y).
(1)求甲、乙两队单独完成任务需要的时间(用含x,y的代数式表示);
(2)甲、乙两队哪队先完成任务?
答案:
C
D
A
A
B
D
7. 1
8.
9.
10. 12
11. 2
018.5
(1)
(2)-
13.
(1)解:原式=·
==
=.
(2)解:原式=1+÷
=1+·
=1-
=.
14.
解:原式=
·
=·
=·
=.
当x=3+时,
原式=.
解:原式=·
=
=.
解不等式组,得∴不等式组的整数解为a=2.
当a=2时,
原式==.
(1)解:原式=÷
=·
=.
(2)解:原式=·(x-1)
=·(x-1)
=-.
(3)解:原式=÷
=÷
=÷
=·
=-.
(1)解:原式=
÷
=-·
=·
=
=.
当a4-4a+2=0时,
原式=.
(2)解:原式=·
=·
=.
当x=2时,原式==0.
(3)解:原式=
÷
=÷
=·
=.
当a=时,
原式==1-2.
(4)解:
÷
=
·
=
·
=·
=·
=.
∵a≠0,a≠-1,a≠2,a≠1,
∴a=-2,
当a=-2时,原式==1.
解:(1)设甲队单独完成任务需要t天,则
tx+ty=2,
解得t=.
乙队单独完成任务需要+=(天).
(2)-=-
=-.
∵x≠y,x>0,y>0,∴(x-y)2>0,xy(x+y)>0,
∴-<0,∴甲队先完成任务.
计算(x-1)÷
·x的结果是(
)
A.-x2
B.-1
C.x2
D.1
化简÷
的结果是(
)
A.x-4
B.x+3
C.
D.
化简
÷
的结果为(
)
A.
B.
C.
D.
若代数式
·的化简结果为2a-4,则整式A为(
)
A.a+1
B.a-1
C.-a-1
D.-a+1
如果2a-1=0,那么代数式
·的值是(
)
A.
B.
C.
D.3
小王上山速度为a
km/h,下山原路返回,速度为b
km/h,则小王上下山的平均速度为(
)
A.
km/h
B.
km/h
C.
km/h
D.
km/h
化简:
·=
.
如果a-b=2,那么代数式
·的值为
.
若a2-6a+9与
互为相反数,则
÷(a+b)=
.
已知x+y=4,x-y=,则式子
的值是
.
对于正数x,规定
f(x)=,例如:f(4)==,f
==,则f(2
019)+f(2
018)+…+f(2)+f(1)+f
+…+f
+f
=
.
计算:
(1)÷
=
;
(2)÷
=
.
化简:
(1)
÷;
(2)1+÷
.
先化简,再求值:
÷,其中x=3+.
先化简,再求值:
÷,其中a为不等式组的整数解.
化简:
(1)
÷;
(2)
÷;
(3)÷
.
先化简,再求值:
(1)
÷
,其中a是方程a2-4a+2=0的解.
(2)
÷,其中x=2.
(3)
÷
,其中a=.
(4)化简式子
÷,并在-2,-1,0,1,2中选取一个合适的数作为a的值代入求值.
甲、乙两工程队分别承担一条2千米的公路维修工作,甲队有一半时间每天维修公路x千米,另一半时间每天维修公路y千米.乙队维修前1千米时,每天维修公路x千米,乙队维修后1千米时,每天维修公路y千米(x≠y).
(1)求甲、乙两队单独完成任务需要的时间(用含x,y的代数式表示);
(2)甲、乙两队哪队先完成任务?
答案:
C
D
A
A
B
D
7. 1
8.
9.
10. 12
11. 2
018.5
(1)
(2)-
13.
(1)解:原式=·
==
=.
(2)解:原式=1+÷
=1+·
=1-
=.
14.
解:原式=
·
=·
=·
=.
当x=3+时,
原式=.
解:原式=·
=
=.
解不等式组,得
当a=2时,
原式==.
(1)解:原式=÷
=·
=.
(2)解:原式=·(x-1)
=·(x-1)
=-.
(3)解:原式=÷
=÷
=÷
=·
=-.
(1)解:原式=
÷
=-·
=·
=
=.
当a4-4a+2=0时,
原式=.
(2)解:原式=·
=·
=.
当x=2时,原式==0.
(3)解:原式=
÷
=÷
=·
=.
当a=时,
原式==1-2.
(4)解:
÷
=
·
=
·
=·
=·
=.
∵a≠0,a≠-1,a≠2,a≠1,
∴a=-2,
当a=-2时,原式==1.
解:(1)设甲队单独完成任务需要t天,则
tx+ty=2,
解得t=.
乙队单独完成任务需要+=(天).
(2)-=-
=-.
∵x≠y,x>0,y>0,∴(x-y)2>0,xy(x+y)>0,
∴-<0,∴甲队先完成任务.
