3.3 牛顿第二定律课件 40张PPT

牛顿运动定律
实验结论：
当保持m一定时， a和F成正比关系。
当保持F一定时，a和m成反比关系。
用数学公式可写成：
或者
牛顿第二定律:
（2）数学表达式：
F=kma
当各物理量均选国际单位时，k=1
(3)1N定义：使质量是1kg的物体产生1m/s2加速度的力
叫做1N。
F=ma
(1) 内容： 物体的加速度跟作用力（所受的合力）成正比，跟物体的质量成反比;加速度的方向跟作用力(合力)的方向相同.
1牛=1千克 · 米/秒2
思考：
1、在牛顿第二定律的表达式 F = ma 中，
m 是标量，F 和 a 是矢量。
2、这两个矢量的方向关系是怎么样？
“力是产生加速度的原因”，故加速度 a 的方向和合力 F 的方向是一致的。
即物体的加速度方向由物体所受合力的方向决定。
哪些是矢量，哪些是标量？
加深理解
一、“四性”
①同体性：是指F合、m和a都是对于“同一个物体”而言，解题时确定研究对象和准确的受力分析是关键。
②矢量性：物体加速度a的方向与物体所受合外力F合的方向始终相同。
③瞬时性：牛顿第二定律说明力的瞬时效应能产生加速度，物体的加速度和物体所受的合外力总是同生、同灭、同步变化。
④独立性：作用于物体上的每一个力各自产生的加速度都遵从牛顿第二定律，而物体的实际加速度则是每个力产生的加速度的矢量和。
分力和加速度的各个方向上的分量关系也遵从牛顿第二定律，即：Fx=max, Fy=may
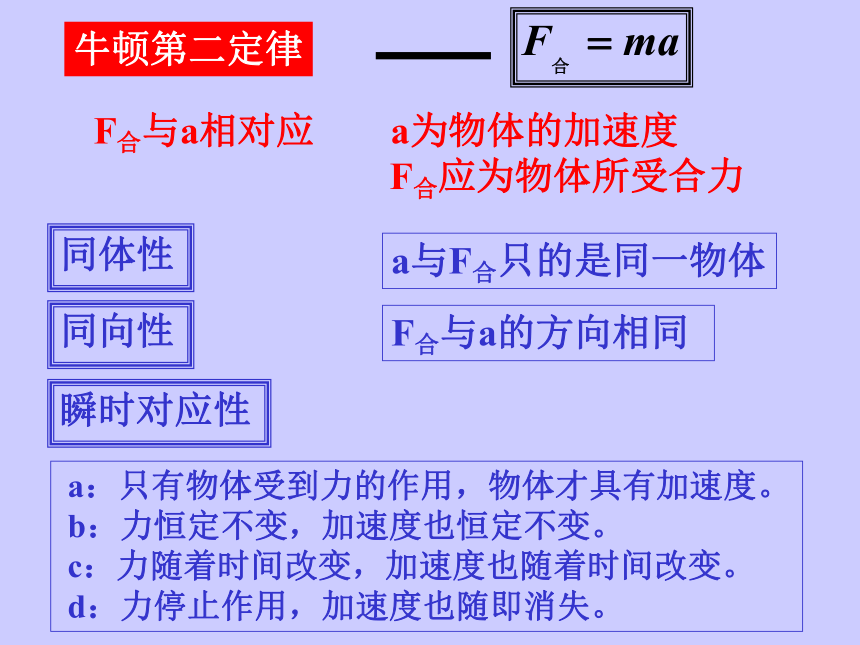
牛顿第二定律
同向性
瞬时对应性
F合与a相对应 a为物体的加速度
F合应为物体所受合力
F合与a的方向相同
a：只有物体受到力的作用，物体才具有加速度。
b：力恒定不变，加速度也恒定不变。
c：力随着时间改变，加速度也随着时间改变。
d：力停止作用，加速度也随即消失。
同体性
a与F合只的是同一物体
二、适用范围：
1、定义式a=△v/ △t ,反映的是速度变化快慢的物理量，速度变化量△v的大小由加速度a和时间△t决定。

2、由牛顿第二只定律可知a=F/m，加速度a由物体所受合外力F和质量m决定；
三、a的定义式和决定式：
1、牛顿第二只定律只适用于惯性参考系，惯性参考系是指相对于地面静止或匀速的参考系；
2、牛顿第二定律只适用于宏观（相对于分子、原子）、低速（远小于光速）运动的物体。
1、下列对牛顿第二定律的表达式F＝ma及其变形公式的理解，正确的是：( )
A、由F＝ma可知，物体所受的合外力与物体的质量成正比，与物体的加速度成反比；
B、由m＝F／a可知，物体的质量与其所受的合外力成正比，与其运动的加速度成反比；
C、由a＝F／m可知，物体的加速度与其所受的合外力成正比，与其质量成反比；
D、由m＝F／a可知，物体的质量可以通过测量它的加速度和它所受到的合外力而求得。
CD
跟 踪 练 习
2、在牛顿第二定律公式F＝kma中，有关比例常数k的说法正确的是（ ）
A、在任何情况下都等于1
B、k值是由质量、加速度和力的大小决定的
C、k值是由质量、加速度和力的单位决定的
D、在国际单位制中，k的数值一定等于1
CD
3、关于运动和力，正确的说法是( )
A、物体速度为零时，合外力一定为零
B、物体作曲线运动，合外力一定是变力
C、物体作直线运动，合外力一定是恒力
D、物体作匀速运动，合外力一定为零
D
4、静止在光滑水平面上的物体，受到一个水平拉力的作用，当力刚开始作用的瞬间，下列说法正确的是 ( )
A.物体同时获得速度和加速度
B.物体立即获得加速度，但速度仍为零
C.物体立即获得速度，但加速度仍为零
D.物体的速度和加速度都仍为零
B
（1）确定研究对象；
（2）进行受力分析和运动状态分析，画出受力的示意图；
（3）建立坐标系，即选取正方向，根据定律列方程；
（4）统一已知量单位，代值求解；
（5）检查所得结果是否符合实际，舍去不合理的解.
用牛顿第二定律解题的一般方法和步骤：
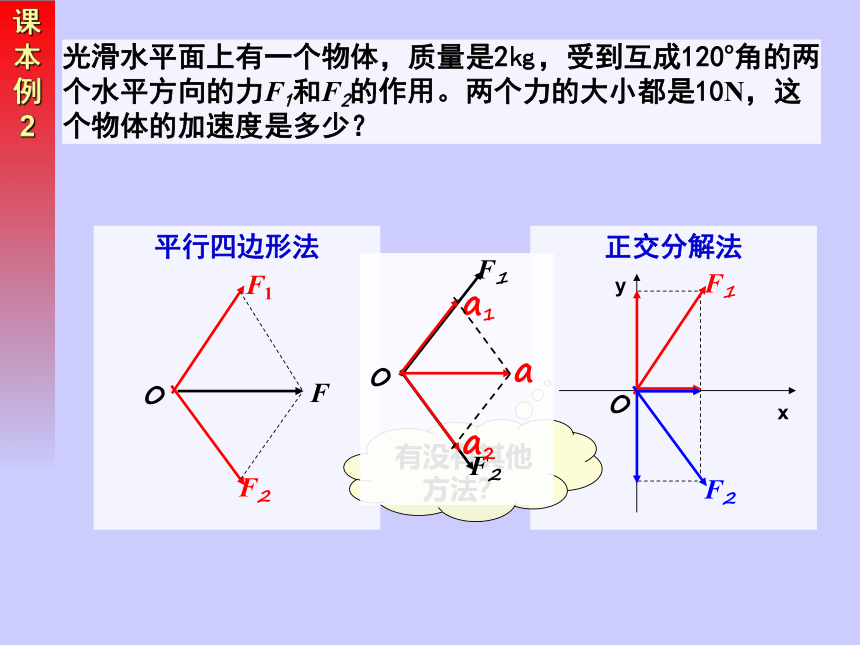
正交分解法
平行四边形法
课本例2
F1
F2
0
F
x
y
0
F1
F2
有没有其他方法？
0
F1
F2
a2
a1
a
光滑水平面上有一个物体，质量是2㎏，受到互成120o角的两个水平方向的力F1和F2的作用。两个力的大小都是10N，这个物体的加速度是多少？
解法1：直接求F1和的F2合力，然后用牛顿第二定律求加速度。
由平行四边形定则可知，F1、F2、F合 构成了一个等边三角形，故
F合 =10 N
a = F合 /m =（10/2 ）m/s2= 5 m/s2
加速度的方向和合力方向相同。
F合
F2
F1
光滑水平面上有一个物体，质量是2㎏，受到互成120o角的两个水平方向的力F1和F2的作用。两个力的大小都是10N，这个物体的加速度是多少？
课本例2
解法2：建立如图直角坐标系
x
y
0
F1
F2
课本例2
把力 和 分别沿x轴和y轴的方向分解.
的两个分力为：
的两个分力为：
和 大小相等，方向相反，相互抵消，
和 的方向相同，所以：
已知合力F合和质量m，据F合＝ma，即可求得：
例、地面上放一木箱，质量为40kg，用100N的力与水平方向成37°角推木箱，如图所示，恰好使木箱匀速前进，求物体受到的摩擦力和支持力。
若用此力与水平方向成37°角斜向上拉木箱，木箱的加速度多大？（取g=10m/s2 ，sin37°=0.6，cos37°=0.8）
3、解：(1)对物体受力分析如图所示，建立直角坐标系，将力F分解。
由物体匀速有：
X轴方向：
Y轴方向：
联立以上方程并带入数据得：

(2)设动摩擦因数为μ，则由F=μN可得：
μ=f/N=80N/460N=4/23=0.174
力F斜向上拉物体，设物体的加速度为a,受力分析如图：
X轴方向：
Y轴方向：
联立以上方程并带入数据
可解得: a=0.52m/s2
N
f
F
F1
G
F2
x
y
N
f

F

F1
F2
G
y
x
F2
变式 自动扶梯与水平面夹角为θ，上面站着质量为m的人，当自动扶梯以加速度a加速向上运动时，求扶梯对人的弹力FN和扶梯对人的摩擦力Ff.
解析　解法一：建立如下图所示的直角坐标系，人的加速度方向正好沿x轴正方向，由题意可得
x轴方向：Ffcos θ+FNsin θ-mgsin θ=ma
y轴方向：FNcos θ-Ffsin θ-mgcos θ=0
解得FN=mg+masin θ，Ff=macos θ.
解法二：建立如右图所示的直角坐标系(水平向右为x轴正方向，竖直向上为y轴正方向)．由于人的加速度方向是沿扶梯向上的，这样建立直角坐标系后，在x轴方向和y轴方向上各有一个加速度的分量，
其中x轴方向的加速度分量ax=acos θ，
y轴方向的加速度分量ay=asin θ，
根据牛顿第二定律有
x轴方向：Ff=max；y轴方向：FN-mg=may
解得FN=mg+masin θ，Ff=macos θ.
思考与讨论：
如图,小明用力拉地面上的箱子,但箱子没动,请思考:
根据牛顿第二定律,有力就能产生加速度,但为什么箱子一直没动呢?
F=ma,其中的F表示合力
【思考1】在光滑的水平面上做匀加速直线运
动的物体,当它所受的合力逐渐减小而方向不
变时，则物体的（ ）
A、加速度越来越大，速度越来越大
B、加速度越来越小，速度越来越小
C、加速度越来越大，速度越来越小
D、加速度越来越小，速度越来越大
反思：对力、加速度、速度之间的关系要有
深刻分析。加速度的大小与合力成正比，方
向与合力方向相同。速度的大小与合力无必
然联系，但物体所受合力不为零时速度必发
生变化。
D
【思考2】质量为m的滑块沿倾角为θ的斜面
下滑，滑块与斜面间的动摩擦因数为μ，求
滑块下落的加速度？
v
正交分解法
反思：解这类问题时，常用正交分解法解题，
建立坐标系时常时加速度的方向为某一坐标
轴的正方向，则另一坐标轴的合力必为零。
（1）物块沿光滑斜面上滑
的加速度为多大？
（2）物块沿粗糙斜面上滑
的加速度是多大？
牛顿运动定律
短跑运动员在起跑时的好坏，对于取得好成绩十分关键，因此，发令枪响必须奋力蹬起跑器，发挥自己的最大体能，以获得最大的加速度，在最短的时间内达到最大的运动速度.
起跑快的运动员有什么特点？
赛车被设计成质量小、发动机牵引力大的结构
【思考】如图所示，一根劲度系数为k的弹簧一端固定于墙面，另一端与质量为m的物体连接着放在光滑水平面上，弹簧原长L0 ,物体被两条细线固定住，细线的长度为L,当同时剪断两条细线的瞬间物体的加速度是多少？（ L0 > L ）
应用牛顿第二定律分析瞬时问题
例 如图所示，质量分别为mA和mB的A和B两球用轻弹簧连接，A球用细绳悬挂起来，两球均处于静止状态．如果将悬挂A球的细线剪断，此时A和B两球的瞬时加速度各是多少？
在应用牛顿第二定律求解物体的瞬时加速度时，经常会遇到轻绳、轻杆、轻弹簧和橡皮绳这些常见的力学模型．
全面准确地理解它们的特点:
1．这些模型的共同点：都是质量可忽略的理想化模型，都会发生形变而产生弹力，同一时刻内部弹力处处相等且与运动状态无关．
2．这些模型的不同点：
(1)轻绳：只能产生拉力，且方向一定沿着绳子背离受力物体，不能承受压力；认为绳子不可伸长，即无论绳子所受拉力多大，长度不变(只要不被拉断)；绳子的弹力可以发生突变——瞬时产生，瞬时改变，瞬时消失．
(2)轻杆：既能承受拉力，又可承受压力，施力或受力方向不一定沿着杆；认为杆既不可伸长，也不可缩短，杆的弹力也可以发生突变．
(3)轻弹簧：既能承受拉力，也可承受压力，力的方向沿弹簧的轴线，受力后发生较大形变，弹簧的长度既可变长，又可变短，遵循胡克定律；因形变量较大，产生形变或使形变消失都有一个过程，故弹簧的弹力不能突变，在极短时间内可认为弹力不变．
(4)橡皮条：只能受拉力，不能承受压力；其长度只能变长，不能变短，同样遵循胡克定律；因形变量较大，产生形变或使形变消失都有一个过程，故橡皮条的弹力同样不能突变.
拓展探究　
(1)例题中将A、B间的弹簧换成弹性橡皮条，如图甲所示，剪断悬挂A球的细线的瞬间，A、B的加速度分别为多大？
(2)在例题中，将A、B之间的轻弹簧与悬挂A球的细绳交换位置，如图乙所示，如果把A、B之间的细绳剪断则A、B两球的瞬时加速度各是多少？
例 两个物体A和B，质量分别为m1和m2，互相接触放在光滑水平面上，如图所示，对物体A施以水平的推力F，则物体A对B的作用力等于_________________.
应用牛顿第二定律对连接体运动问题的讨论
变式训练:用水平恒力F推动放在光滑水平面上、质量均为m的六个紧靠在一起的木块，则第5号木块受到的合外力等于 ，第4号木块对第5号本块的作用力等于 。
F
1
2
3
4
5
6
巩固练习:
如图在光滑地面上，水平外力F拉动小车和木块一起作无相对滑动的加速运动.小车质量是M，木块质量是m，力大小是F，加速度大小是a，木块和小车之间动摩擦因数是μ，则在这个过程中，木块受到的摩擦力大小是（ ）
A. μmg B. ma C. D.F-Ma
如图1-15所示：把质量为M的的物体放在光滑的水平高台上，用一条可以忽略质量而且不变形的细绳绕过定滑轮把它与质量为m的物体连接起来，求：物体M和物体m的运动加速度各是多大？
【思考】质量为m的箱子C，顶端悬挂质量为
m的小球B，B下端通过轻弹簧连一质量为m的小
球A，箱子用轻绳OP悬于天花板。现剪断OP。
在轻绳被剪断瞬间，小球A、B和箱子C的加速度
A、 分别为（ ）
B、
C、
D、
力与加速度的
瞬时对应性
C
A
B
O
P
【思考A】如图所示，当小车静止或水平向右匀速运动时，悬线应处何位置？如果小车向右加速或减速运动时，悬线会处于什么位置？为什么？
【思考B】如图所示，当小车以加速度a水平向右加速运动时，质量为m的小球与小车相对静止时，悬线与竖直方向的夹角为多少？
【思考C】当小车水平向右减速运动时，质量为m的小球悬线与竖直方向的夹角为θ时，试求小车所具有的加速度？
V
a
V
a
【思考5-1】
【思考3】两物体A、B静止于同一水平面上，
与水平面间的动磨擦因数分别为μA μB，
质量为mA、mB。用平行于水平面的力F拉物
体A、B，所得加速度a与拉力F的关系如图
所示，则（ ）
A、
B、
C、
D、
a
A
B
F
反思：
善于从图像中获取信息
斜率与截距的物理意义
B
思考:4-1.一小球从竖直在地面上轻弹簧正上方某处自由落下,试分析小球从刚接触弹簧到被压缩最短过程中小球的速度、加速度怎样变化?
【思考4-3】在沿平直轨道运动的车厢中的光滑
水平桌面上,用弹簧拴着一个小球，弹簧处于
自然伸长状态，如图所示，当旅客看到弹簧
长度变短时，对火车的运动状态下列说法中
正确的是（ ）
A、火车向右加速运动
B、火车向右减速运动
C、火车向左加速运动
D、火车向左减速运动
【思考5-2】如图所示，一质量为M的小车内有一质量为m的物体，设物体与竖直车壁间摩擦因素为μ，试思考小车沿水平方向作什么运动时，物体恰能与后车壁保持相对静止。
思考：光滑水面上，一物体质量为1kg，初速度为0，从0时刻开始受到一水平向右的拉力F，F随时间变化图如下，要求作出速度时间图象。
t/s
F/N
0
1
2
3
1
2
3
4
t(s)
v(m/s)
0
1
2
3
1
2
3
4