4.1 共点力作用下物体的平衡课件 27张PPT
文档属性
| 名称 | 4.1 共点力作用下物体的平衡课件 27张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-10-02 00:00:00 | ||
图片预览






文档简介
第四章 物体的平衡
4.1 共点力作用下物体的平衡
G
N
f静
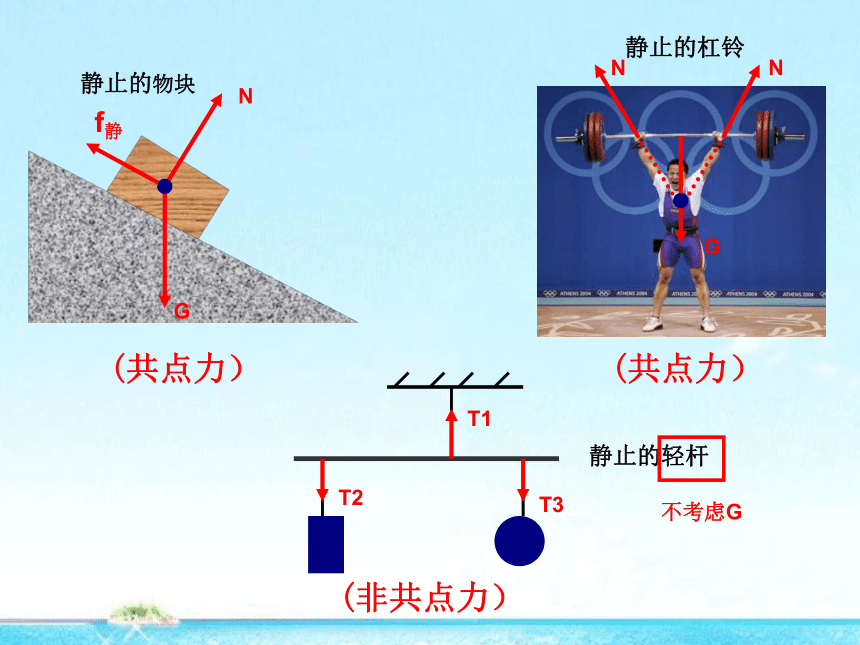
(共点力)
G
N
N
(共点力)
T1
T2
T3
(非共点力)
静止的物块
静止的杠铃
静止的轻杆
不考虑G
一.平衡状态
1.共点力: 如果多个力作用在物体的同一点,或者它们的作用线 相交于一点,这几个力叫做共点力
书写笔记
?
平衡小实验:
一.平衡状态
1.共点力: 如果多个力作用在物体的同一点,或者它们的作用线 相交于一点,这几个力叫做共点力
书写笔记
2.平衡状态:物体处于静止或者匀速直线运动的状态叫做平衡状态。
a=0
3.平衡状态的分类
静态平衡:物体保持静止、匀速状态
动态平衡:物体缓慢移动
例1. 判断:以下物体是否处于平衡状态?
(1) 天花板下悬挂的静止的吊扇。
(2) 粗糙斜面上静止的木块。
(3) 光滑水平面上匀速直线滑动的冰块。
(4) 沿斜面匀速直线下滑的铁箱。
(5) 竖直上抛到最高点的篮球。
(6) 拿在手上铅球,松手的瞬间。
答:(1)(2) (3)(4)是平衡状态.
(5)(6)不是平衡状态.
是
是
是
是
V=0
不是
不是
注意:保持静止 和 瞬时速度为0 不同
二.平衡条件
对下列处于静止状态的物体受力分析
G
N
G
N
二.平衡条件
对下列处于静止状态的物体受力分析
G
N
G
N
(小实验)
结论:当物体在二个力的作用下处于平衡状态时,这二个力一定是等值、反向、共线;
二.平衡条件
G
N
G
N
(小实验)
结论:二力平衡时:两个力等大、反向、共线
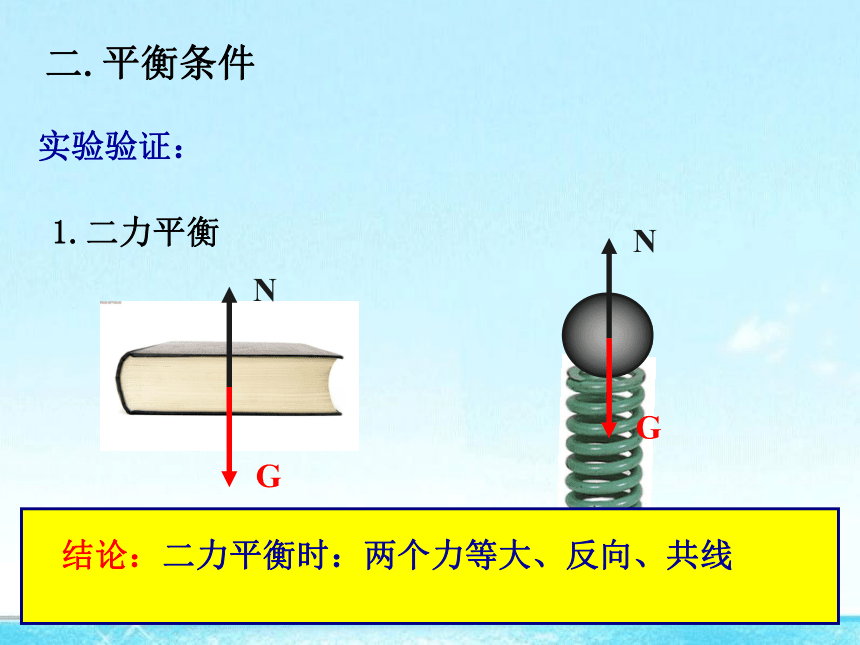
1.二力平衡
二.平衡条件
1.二力平衡:两个力等大、反向、共线
二.平衡条件
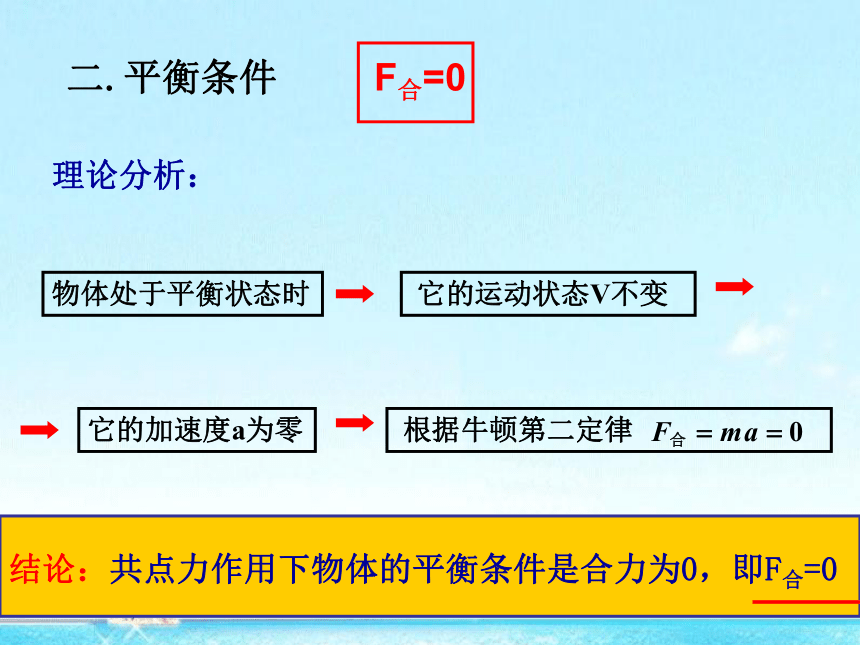
物体处于平衡状态时
它的运动状态V不变
它的加速度a为零
根据牛顿第二定律
二.平衡条件
G
N
G
N
(小实验)
结论:二力平衡时:两个力等大、反向、共线
1.二力平衡
二.平衡条件
1.二力平衡: 两个力等大、反向、共线
二.平衡条件
物体处于平衡状态时
它的运动状态V不变
它的加速度a为零
根据牛顿第二定律
F合=0
二.平衡条件
物体处于平衡状态时
它的运动状态V不变
它的加速度a为零
根据牛顿第二定律
F合=0
理论分析:
结论:共点力作用下物体的平衡条件是合力为0,即F合=0
二.平衡条件
物体处于平衡状态时
它的运动状态V不变
它的加速度a为零
根据牛顿第二定律
F合=0
理论分析:
结论:共点力作用下物体的平衡条件是合力为0,即F合=0
一.平衡状态
1.共点力: 如果多个力作用在物体的同一点,或者它们的作用线 相交于一点,这几个力叫做共点力
书写笔记
2.平衡状态:物体处于静止或者匀速直线运动的状态叫做平衡状态。
a=0
3.平衡状态的分类
静态平衡:物体保持静止、匀速状态
动态平衡:物体缓慢移动
二.平衡条件: F合= 0
1.二力平衡: 两个力等大、反向、共线
书写笔记
2.三力平衡:
实验探究:三力平衡条件
1.设计实验方案
2.实验器材:弹簧秤两只,200g钩码两只,细线等,在竖直面内完成
实验探究:三力平衡条件
1. 设计实验方案
2. 实验器材:弹簧秤两只,
200g钩码两只,细线等,
在竖直面内完成
F1
F3
F2
F23
3. 实验结论:任意两个力的合力与第三个力大小相等,方向相反,作用在同一直线上
实验探究:三力平衡条件
1. 设计实验方案
2. 实验器材:弹簧秤两只,
200g钩码两只,细线等,
在竖直面内完成
F1
F3
F2
F23
3. 实验结论:任意两个力的合力与第三个力大小相等,方向相反,作用在同一直线上
实验探究:三力平衡条件
1. 设计实验方案
2. 实验器材:弹簧秤两只,
200g钩码两只,细线等,
在竖直面内完成
F1
F3
F2
F23
3. 实验结论:任意两个力的合力与第三个力等大,反向。
二.平衡条件: F合= 0
1.二力平衡: 两个力等大、反向、共线
书写笔记
2.三力平衡:
二.平衡条件: F合= 0
1.二力平衡: 两个力等大、反向、共线
书写笔记
2.三力平衡:任意两个力的合力与第三个力等大,反向。
二.平衡条件: F合= 0
1.二力平衡: 两个力等大、反向、共线
书写笔记
2.三力平衡:任意两个力的合力与第三个力等大、反向。
3.多力平衡:
任意一个力与其余各力的合力等大、反向
二.平衡条件: F合= 0
1.二力平衡: 两个力等大、反向、共线
书写笔记
2.三力平衡:任意两个力的合力与第三个力等大、反向。
3.多力平衡:
任意一个力与其余各力的合力等大、反向
F1
F2
F3
F4
F5
第四章 物体的平衡
4.1 共点力作用下物体的平衡
1.什是共点力?
2.什么是平衡状态?
3.平衡条件是什么?
4.平衡问题的一般解法?
G
N
f静
(共点力)
G
N
N
(共点力)
T1
T2
T3
(非共点力)
静止的物块
静止的杠铃
静止的轻杆
不考虑G
一.平衡状态
1.共点力: 如果多个力作用在物体的同一点,或者它们的作用线 相交于一点,这几个力叫做共点力
书写笔记
2.平衡状态:物体处于静止或者匀速直线运动的状态叫做平衡状态。
a=0
3.平衡状态的分类
静态平衡:物体保持静止、匀速状态
动态平衡:物体缓慢移动
速度V不变
一.平衡状态
1.共点力: 如果多个力作用在物体的同一点,或者它们的作用线 相交于一点,这几个力叫做共点力
书写笔记
2.平衡状态:物体处于静止或者匀速直线运动的状态叫做平衡状态。
a=0
3.平衡状态的分类
静态平衡:物体保持静止、匀速状态
动态平衡:物体缓慢移动
速度V不变
一.平衡状态
1.共点力: 如果多个力作用在物体的同一点,或者它们的作用线 相交于一点,这几个力叫做共点力
书写笔记
2.平衡状态:物体处于静止或者匀速直线运动的状态叫做平衡状态。
a=0
3.平衡状态的分类
静态平衡:物体保持静止、匀速状态
动态平衡:物体缓慢移动
速度V不变
例1. 判断:以下物体是否处于平衡状态?
(1) 天花板下悬挂的静止的吊扇。
(2) 粗糙斜面上静止的木块。
(3) 光滑水平面上匀速直线滑动的冰块。
(4) 沿斜面匀速直线下滑的铁箱。
(5) 竖直上抛到最高点的篮球。
(6) 拿在手上铅球,松手的瞬间。
答:(1)(2) (3)(4)是平衡状态.
(5)(6)不是平衡状态.
是
是
是
是
V=0
不是
不是
注意:保持静止 和 瞬时速度为0 不同
二.平衡条件
物体处于平衡状态时
它的运动状态V不变
它的加速度a为零
根据牛顿第二定律
F合=0
理论分析:
结论:共点力作用下物体的平衡条件是合力为0,即F合=0
例2 如图,某个物体在F1、F2、F3、F4四个力的作用下处于静止状态,若F4的方向沿逆时针转过60°而保持其大小不变,其余三个力的大小和方向均不变,则此时物体所受到的合力大小为( )
例2 如图,某个物体在F1、F2、F3、F4四个力的作用下处于静止状态,若F4的方向沿逆时针转过60°而保持其大小不变,其余三个力的大小和方向均不变,则此时物体所受到的合力大小为( )
F4
F4’
1200
F4
例2 如图,某个物体在F1、F2、F3、F4四个力的作用下处于静止状态,若F4的方向沿逆时针转过60°而保持其大小不变,其余三个力的大小和方向均不变,则此时物体所受到的合力大小为( )
F4
F4’
1200
F4
例2. 如图,某个物体在F1、F2、F3、F4四个力的作用下处于静止状态,若F4的方向沿逆时针转过60°而保持其大小不变,其余三个力的大小和方向均不变,则此时物体所受到的合力大小为( )
F4
F4’
1200
F4
C
三.解决共点力平衡问题的一般方法
二.平衡条件: F合= 0
1.二力平衡: 两个力等大、反向、共线
书写笔记
2.三力平衡:任意两个力的合力与第三个力等大、反向。
3.多力平衡:
任意一个力与其余各力的合力等大、反向
F1
F2
F3
F4
F5
三.解决共点力平衡问题的一般方法
1.正交分解法
F合=0
X:FX合=0
Y:FY合=0
书写笔记
例3.
例2. 如图,某个物体在F1、F2、F3、F4四个力的作用下处于静止状态,若F4的方向沿逆时针转过60°而保持其大小不变,其余三个力的大小和方向均不变,则此时物体所受到的合力大小为( )
F4
F4’
1200
F4
C
简化为二力平衡
例2. 如图,某个物体在F1、F2、F3、F4四个力的作用下处于静止状态,若F4的方向沿逆时针转过60°而保持其大小不变,其余三个力的大小和方向均不变,则此时物体所受到的合力大小为( )
F4
F4’
1200
F4
C
简化为二力平衡
F合=0
例2. 如图,某个物体在F1、F2、F3、F4四个力的作用下处于静止状态,若F4的方向沿逆时针转过60°而保持其大小不变,其余三个力的大小和方向均不变,则此时物体所受到的合力大小为( )
F4
F4’
1200
F4
C
简化为二力平衡
F合=0
θ
例3.
m
静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.竖直挡板对小球的支持力
mg
N1
N2
x
y
θ
θ
m
θ
例3.
m
静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.竖直挡板对小球的支持力
mg
N1
N2
x
y
θ
X:
N2=N1 sinθ
Y:
N1 cos θ=mg
N1=mg/ cos θ
N2=mg tan θ
θ
例3.
m
静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.竖直挡板对小球的支持力
mg
N1
N2
x
y
θ
X:
N2=N1 sinθ
Y:
N1 cos θ=mg
N1=mg/ cos θ
N2=mg tan θ
θ
例3.
m
静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.竖直挡板对小球的支持力
mg
N1
N2
x
y
θ
X:
N2=N1 sinθ
Y:
N1 cos θ=mg
N1=mg/ cos θ
N2=mg tan θ
解题步骤:
(1)明确研究对象.
(2)受力分析
θ
例3.
m
静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.竖直挡板对小球的支持力
mg
N1
N2
x
y
θ
X:
N2=N1 sinθ
Y:
N1 cos θ=mg
N1=mg/ cos θ
N2=mg tan θ
解题步骤:
(1)明确研究对象.
(2)受力分析
(3) 建立直角坐标系,正交分解.
(4)根据Fx合=0,Fy合=0,列方程求解.
θ
例3.
m
静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.竖直挡板对小球的支持力
mg
N1
N2
x
y
θ
X:
N2=N1 sinθ
Y:
N1 cos θ=mg
N1=mg/ cos θ
N2=mg tan θ
解题步骤:
(1)明确研究对象.
(2)受力分析
(3) 建立直角坐标系,正交分解.
(4)根据Fx合=0,Fy合=0,列方程求解.
θ
m
例3.静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.竖直挡板对小球的支持力
mg
N1
N2
x
y
θ
X:
N2=N1 sinθ
Y:
N1 cos θ=mg
N1=mg/ cos θ
N2=mg tan θ
解题步骤:
(1)明确研究对象.
(2)受力分析
(3)建立直角坐标系,正交分解.
(4)根据Fx合=0,Fy合=0,列方程求解.
θ
m
例4.
θ
m
例3.静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.竖直挡板对小球的支持力
mg
N1
N2
x
y
θ
X:
N2=N1 sinθ
Y:
N1 cos θ=mg
N1=mg/ cos θ
N2=mg tan θ
解题步骤:
(1)明确研究对象.
(2)受力分析.
(3)建立直角坐标系,正交分解.
(4)根据Fx合=0,Fy合=0,列方程求解.
θ
m
例3.静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.竖直挡板对小球的支持力
mg
N1
N2
x
y
θ
X:
N2=N1 sinθ
Y:
N1 cos θ=mg
N1=mg/ cos θ
N2=mg tan θ
解题步骤:
(1)明确研究对象.
(2)受力分析.
(3)建立直角坐标系,正交分解.
(4)根据Fx合=0,Fy合=0,列方程求解.
θ
m
例4.静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.竖直挡板对小球的支持力
G
N1
N2
N1
N2
θ
m
例3.静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.竖直挡板对小球的支持力
mg
N1
N2
X:
N2=N1 sinθ
Y:
N1 cos θ=mg
N1=mg/ cos θ
N2=mg tan θ
θ
m
例4.静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.竖直挡板对小球的支持力
mg
N1
N2
N1
N2
θ
=mg cos θ
=mg sin θ
θ
m
例3.静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.竖直挡板对小球的支持力
mg
N1
N2
X:
N2=N1 sinθ
Y:
N1 cos θ=mg
N1=mg/ cos θ
N2=mg tan θ
N1
N2
θ
=mg/ cos θ
=mg tan θ
三.解决共点力平衡问题的一般方法
1.正交分解法
F合=0
X:FX合=0
Y:FY合=0
书写笔记
2.三角形法
适用于:一切平衡
适用于:三力平衡,且有两力垂直
三.解决共点力平衡问题的一般方法
1.正交分解法
F合=0
X:FX合=0
Y:FY合=0
书写笔记
2.三角形法
适用于:一切平衡
适用于:三力平衡,且有两力垂直
例5.如图,AO,BO,和CO三根绳子能承受的最大拉力相等,0为结 点,BO与竖直方向夹角为300,悬挂物质量为m.
求:OA,OB两根绳子拉力的大小
O
A
B
C
300
例5.如图,AO,BO,和CO三根绳子能承受的最大拉力相等,0为结 点,BO与竖直方向夹角为θ=300 ,悬挂物质量为m.
求:OA,OB两根绳子拉力的大小
O
A
B
C
θ
mg
TOB
TOA
问题1:增大m,那根绳先断?
TOB
TOA
300
问题2:若B点不动,A点上 移,TOA,TOB将怎样变?
一直减小
先减小后增大
θ
m
mg
N1
N2
N1
N2
?
?
缓慢
一直减小
一直增大
θ
m
例3.静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.竖直挡板对小球的支持力
mg
N1
N2
X:
N2=N1 sinθ
Y:
N1 cos θ=mg
N1=mg/ cos θ
N2=mg tan θ
N1
N2
θ
=mg/ cos θ
=mg tan θ
三.解决共点力平衡问题的一般方法
1.正交分解法
F合=0
X:FX合=0
Y:FY合=0
书写笔记
2.三角形法
适用于:一切平衡
适用于:三力平衡,且有两力垂直
θ
m
mg
N1
N2
N1
N2
?
?
缓慢
一直减小
一直增大
例5.如图,AO,BO,和CO三根绳子能承受的最大拉力相等,0为结 点,BO与竖直方向夹角为θ=300 ,悬挂物质量为m.
求:OA,OB两根绳子拉力的大小
O
A
B
C
θ
mg
TOB
TOA
问题1:增大m,那根绳先断?
TOB
TOA
300
问题2:若B点不动,A点上 移,TOA,TOB将怎样变?
一直减小
先减小后增大
动态三角形法,解动态平衡问题
θ
m
mg
N1
N2
N1
N2
缓慢
?
?
一直减小
先减小后增大
三.解决共点力平衡问题的一般方法
1.正交分解法
F合=0
X:FX合=0
Y:FY合=0
书写笔记
2.三角形法
适用于:一切平衡
适用于:三力平衡,且有两力垂直
例5.如图,AO,BO,和CO三根绳子能承受的最大拉力相等,0为结 点,BO与竖直方向夹角为θ=300 ,悬挂物质量为m.
求:OA,OB两根绳子拉力的大小
O
A
B
C
θ
mg
TOB
TOA
问题1:增大m,那根绳先断?
TOB
TOA
300
问题2:若B点不动,A点上 移,TOA,TOB将怎样变?
一直减小
先减小后增大
三角形法,解动态平衡问题
三.解决共点力平衡问题的一般方法
1.正交分解法
F合=0
X:FX合=0
Y:FY合=0
书写笔记
2.三角形法
适用于:一切平衡
适用于:三力平衡,且有两力垂直
三.解决共点力平衡问题的一般方法
1.正交分解法
F合=0
X:FX合=0
Y:FY合=0
书写笔记
2.三角形法
适用于:一切平衡
适用于:三力平衡,且有两力垂直
3、三角形法---解动态平衡问题
例6.如图所示,一个重为G的圆球,被一段细绳挂在竖直光滑墙上,绳与竖直墙的夹角为α,则绳子的拉力和墙壁对球的弹力各是多少?
α
第四章 物体的平衡
4.1 共点力作用下物体的平衡
1.什是共点力?
2.什么是平衡状态?
3.平衡条件是什么?
4.平衡问题的一般解法?
课堂小结
1.什是共点力?
2.什么是平衡状态?
3.平衡条件是什么?
4.平衡问题的一般解法?
课堂小结
1.什是共点力?
2.什么是平衡状态?
3.平衡条件是什么?
4.平衡问题的一般解法?
解决了以下四个问题:
练习1.如图所示,一个重为G的圆球,被一段细绳挂在竖直光滑 墙上,绳与竖直墙的夹角为α,则
( 1 )绳子的拉力T和墙壁对球的弹力N各是多少?
( 2 )若绳子变长,T、N将怎样变化?
α
练习2、在水平路面上用绳子拉一只重100N的箱子,绳子和路面的夹角为37°,如图所示.当绳子的拉力为50N,恰好使箱子匀速移动。
求1.箱子受到的摩擦力
2.箱子和地面间的动摩擦因数.
37o
F
练习2、在水平路面上用绳子拉一只重100N的箱子,绳子和路面的夹角为37°,如图所示.当绳子的拉力为50N,恰好使箱子匀速移动。求:
( 1 )箱子受到的摩擦力
( 2 )箱子和地面间的动摩擦因数.
37o
F
例5.如图,AO,BO,和CO三根绳子能承受的最大拉力相等,0为结 点,BO与竖直方向夹角为θ=300 ,悬挂物质量为m.
求:OA,OB两根绳子拉力的大小
O
A
B
C
θ
mg
TOB
TOA
问题1:增大m,那根绳先断?
TOB
TOA
300
问题2:若B点不动,A点上 移,TOA,TOB将怎样变?
一直减小
先减小后增大
三角形法,解动态平衡问题
拓展:
练习1、在水平路面上用绳子拉一只重100N的箱子,绳子和路面的夹角为37°,如图所示.当绳子的拉力为50N,恰好使箱子匀速移动。求:
( 1 )箱子受到的摩擦力
( 2 )箱子和地面间的动摩擦因数.
37o
F
练习2.如图所示,一个重为G的圆球,被一段细绳挂在竖直光滑 墙上,绳与竖直墙的夹角为α,则
( 1 )绳子的拉力T和墙壁对球的弹力N各是多少?
( 2 )若绳子变长,T、N将怎样变化?
α
练习3.物体A在水平力F1=400N的作用下,沿倾角θ=60°的斜面匀速下滑,如图所示。物体A受的重力G=400N,求:
(1)斜面对物体A的支持力
(2)A与斜面间的动摩擦因数μ.
A
F1
60°
练习1、如图所示,质量为m的物体在恒力F作用下,沿水平天花板向右做匀速直线运动.力F与水平方向的夹角为θ,重力加速度为g.则物体与天花板间的动摩擦因数μ=________.
练习3.如图所示,细绳CO与竖直方向成30°角,A、B两物体用跨过滑轮的细绳相连,已知物体B所受到的重力为100N,地面对物体B的支持力为80N,试求:
(1)物体A所受到的重力;
(2)物体B与地面间的摩擦力;
(3)细绳CO受到的拉力。
同学们,再见!
第四章 物体的平衡
4.1 共点力作用下物体的平衡
1.什么是共点力?
2.什么是平衡状态?
3.平衡条件是什么?
4.平衡问题的一般解法?
一.平衡状态
1.共点力: 如果多个力作用在同一点,或者它们的作用线 相交于一点,这几个力叫做共点力
书写笔记
?
θ
m
例4.静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.挡板对小球的支持力
mg
N1
N2
N1
N2
θ
=mg cos θ
=mg sin θ
例5.如图,AO,BO,和CO三根绳子能承受的最大拉力相等,0为结 点,BO与竖直方向夹角为θ=300 ,悬挂物质量为m.
求:OA,OB两根绳子拉力的大小
O
A
B
C
θ
mg
TOB
TOA
问题1:增大m,那根绳先断?
TOB
TOA
300
问题2:若B点不动,A点缓慢上移,TOA,TOB将怎样变?
一直减小
先减小后增大
三角形法,解动态平衡问题
拓展:
练习1、如图所示,质量为m的物体在恒力F作用下,沿水平天花板向右做匀速直线运动.力F与水平方向的夹角为θ,重力加速度为g.则物体与天花板间的动摩擦因数μ=________.
练习3.如图所示,细绳CO与竖直方向成30°角,A、B两物体用跨过滑轮的细绳相连,已知物体B所受到的重力为100N,地面对物体B的支持力为80N,试求:
(1)物体A所受到的重力;
(2)物体B与地面间的摩擦力;
(3)细绳CO受到的拉力。
一.平衡状态
1.共点力: 如果多个力作用在物体的同一点,或者它们的作用线 相交于一点,这几个力叫做共点力
书写笔记
2.平衡状态:物体处于静止或者匀速直线运动的状态叫做平衡状态。
a=0
3.平衡状态的分类
静态平衡:保持静止
动态平衡:匀速直线、
速度V不变
物体缓慢运动
θ
m
例3.静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.竖直挡板对小球的支持力
mg
N1
N2
X:
N2=N1 sinθ
Y:
N1 cos θ=mg
N1=mg/ cos θ
N2=mg tan θ
N1
N2
θ
=mg/ cos θ
=mg tan θ
例5.如图,AO,BO,和CO三根绳子能承受的最大拉力相等,0为结 点,BO与竖直方向夹角为θ=300 ,悬挂物质量为m.
求:OA,OB两根绳子拉力的大小
O
A
B
C
θ
mg
TOB
TOA
问题1:增大m,那根绳先断?
TOB
TOA
300
问题2:若B点不动,A点缓慢上移,TOA,TOB将怎样变?
一直减小
先减小后增大
三角形法,解动态平衡问题
拓展:
θ
m
mg
N1
N2
N1
N2
?
?
缓慢
一直减小
一直增大
θ
m
mg
N1
N2
N1
N2
缓慢
?
?
一直减小
先减小后增大
课堂小结
1.什么是共点力?
2.什么是平衡状态?
3.平衡条件是什么?
4.平衡问题的一般解法?
解决了以下四个问题:
一.平衡状态
1.共点力: 如果多个力作用在物体的同一点,或者它们的作用线 相交于一点,这几个力叫做共点力
书写笔记
2.平衡状态:物体处于静止或者匀速直线运动的状态
a=0
3.平衡状态的分类
静态平衡:保持静止
动态平衡:匀速直线、
速度V不变
物体缓慢运动
二.平衡条件
G
N
G
N
实验验证:
结论:二力平衡时:两个力等大、反向、共线
1.二力平衡
二.平衡条件
G
N
G
N
实验验证:
结论:二力平衡时:两个力等大、反向、共线
1.二力平衡
例5.如图,AO,BO,和CO三根绳子能承受的最大拉力相等,0为结 点,BO与竖直方向夹角为θ=300 ,悬挂物质量为m.
求:OA,OB两根绳子拉力的大小
O
A
B
C
θ
mg
TOB
TOA
问题1:增大m,哪根绳先断?
TOB
TOA
300
问题2:若B点不动,A点缓慢上移,TOA,TOB将怎样变?
一直减小
先减小后增大
三角形法,解动态平衡问题
拓展:
θ
m
mg
N1
N2
N1
N2
?
?
缓慢
一直减小
一直增大
θ
m
mg
N1
N2
N1
N2
缓慢
?
?
一直减小
先减小后增大
4.1 共点力作用下物体的平衡
G
N
f静
(共点力)
G
N
N
(共点力)
T1
T2
T3
(非共点力)
静止的物块
静止的杠铃
静止的轻杆
不考虑G
一.平衡状态
1.共点力: 如果多个力作用在物体的同一点,或者它们的作用线 相交于一点,这几个力叫做共点力
书写笔记
?
平衡小实验:
一.平衡状态
1.共点力: 如果多个力作用在物体的同一点,或者它们的作用线 相交于一点,这几个力叫做共点力
书写笔记
2.平衡状态:物体处于静止或者匀速直线运动的状态叫做平衡状态。
a=0
3.平衡状态的分类
静态平衡:物体保持静止、匀速状态
动态平衡:物体缓慢移动
例1. 判断:以下物体是否处于平衡状态?
(1) 天花板下悬挂的静止的吊扇。
(2) 粗糙斜面上静止的木块。
(3) 光滑水平面上匀速直线滑动的冰块。
(4) 沿斜面匀速直线下滑的铁箱。
(5) 竖直上抛到最高点的篮球。
(6) 拿在手上铅球,松手的瞬间。
答:(1)(2) (3)(4)是平衡状态.
(5)(6)不是平衡状态.
是
是
是
是
V=0
不是
不是
注意:保持静止 和 瞬时速度为0 不同
二.平衡条件
对下列处于静止状态的物体受力分析
G
N
G
N
二.平衡条件
对下列处于静止状态的物体受力分析
G
N
G
N
(小实验)
结论:当物体在二个力的作用下处于平衡状态时,这二个力一定是等值、反向、共线;
二.平衡条件
G
N
G
N
(小实验)
结论:二力平衡时:两个力等大、反向、共线
1.二力平衡
二.平衡条件
1.二力平衡:两个力等大、反向、共线
二.平衡条件
物体处于平衡状态时
它的运动状态V不变
它的加速度a为零
根据牛顿第二定律
二.平衡条件
G
N
G
N
(小实验)
结论:二力平衡时:两个力等大、反向、共线
1.二力平衡
二.平衡条件
1.二力平衡: 两个力等大、反向、共线
二.平衡条件
物体处于平衡状态时
它的运动状态V不变
它的加速度a为零
根据牛顿第二定律
F合=0
二.平衡条件
物体处于平衡状态时
它的运动状态V不变
它的加速度a为零
根据牛顿第二定律
F合=0
理论分析:
结论:共点力作用下物体的平衡条件是合力为0,即F合=0
二.平衡条件
物体处于平衡状态时
它的运动状态V不变
它的加速度a为零
根据牛顿第二定律
F合=0
理论分析:
结论:共点力作用下物体的平衡条件是合力为0,即F合=0
一.平衡状态
1.共点力: 如果多个力作用在物体的同一点,或者它们的作用线 相交于一点,这几个力叫做共点力
书写笔记
2.平衡状态:物体处于静止或者匀速直线运动的状态叫做平衡状态。
a=0
3.平衡状态的分类
静态平衡:物体保持静止、匀速状态
动态平衡:物体缓慢移动
二.平衡条件: F合= 0
1.二力平衡: 两个力等大、反向、共线
书写笔记
2.三力平衡:
实验探究:三力平衡条件
1.设计实验方案
2.实验器材:弹簧秤两只,200g钩码两只,细线等,在竖直面内完成
实验探究:三力平衡条件
1. 设计实验方案
2. 实验器材:弹簧秤两只,
200g钩码两只,细线等,
在竖直面内完成
F1
F3
F2
F23
3. 实验结论:任意两个力的合力与第三个力大小相等,方向相反,作用在同一直线上
实验探究:三力平衡条件
1. 设计实验方案
2. 实验器材:弹簧秤两只,
200g钩码两只,细线等,
在竖直面内完成
F1
F3
F2
F23
3. 实验结论:任意两个力的合力与第三个力大小相等,方向相反,作用在同一直线上
实验探究:三力平衡条件
1. 设计实验方案
2. 实验器材:弹簧秤两只,
200g钩码两只,细线等,
在竖直面内完成
F1
F3
F2
F23
3. 实验结论:任意两个力的合力与第三个力等大,反向。
二.平衡条件: F合= 0
1.二力平衡: 两个力等大、反向、共线
书写笔记
2.三力平衡:
二.平衡条件: F合= 0
1.二力平衡: 两个力等大、反向、共线
书写笔记
2.三力平衡:任意两个力的合力与第三个力等大,反向。
二.平衡条件: F合= 0
1.二力平衡: 两个力等大、反向、共线
书写笔记
2.三力平衡:任意两个力的合力与第三个力等大、反向。
3.多力平衡:
任意一个力与其余各力的合力等大、反向
二.平衡条件: F合= 0
1.二力平衡: 两个力等大、反向、共线
书写笔记
2.三力平衡:任意两个力的合力与第三个力等大、反向。
3.多力平衡:
任意一个力与其余各力的合力等大、反向
F1
F2
F3
F4
F5
第四章 物体的平衡
4.1 共点力作用下物体的平衡
1.什是共点力?
2.什么是平衡状态?
3.平衡条件是什么?
4.平衡问题的一般解法?
G
N
f静
(共点力)
G
N
N
(共点力)
T1
T2
T3
(非共点力)
静止的物块
静止的杠铃
静止的轻杆
不考虑G
一.平衡状态
1.共点力: 如果多个力作用在物体的同一点,或者它们的作用线 相交于一点,这几个力叫做共点力
书写笔记
2.平衡状态:物体处于静止或者匀速直线运动的状态叫做平衡状态。
a=0
3.平衡状态的分类
静态平衡:物体保持静止、匀速状态
动态平衡:物体缓慢移动
速度V不变
一.平衡状态
1.共点力: 如果多个力作用在物体的同一点,或者它们的作用线 相交于一点,这几个力叫做共点力
书写笔记
2.平衡状态:物体处于静止或者匀速直线运动的状态叫做平衡状态。
a=0
3.平衡状态的分类
静态平衡:物体保持静止、匀速状态
动态平衡:物体缓慢移动
速度V不变
一.平衡状态
1.共点力: 如果多个力作用在物体的同一点,或者它们的作用线 相交于一点,这几个力叫做共点力
书写笔记
2.平衡状态:物体处于静止或者匀速直线运动的状态叫做平衡状态。
a=0
3.平衡状态的分类
静态平衡:物体保持静止、匀速状态
动态平衡:物体缓慢移动
速度V不变
例1. 判断:以下物体是否处于平衡状态?
(1) 天花板下悬挂的静止的吊扇。
(2) 粗糙斜面上静止的木块。
(3) 光滑水平面上匀速直线滑动的冰块。
(4) 沿斜面匀速直线下滑的铁箱。
(5) 竖直上抛到最高点的篮球。
(6) 拿在手上铅球,松手的瞬间。
答:(1)(2) (3)(4)是平衡状态.
(5)(6)不是平衡状态.
是
是
是
是
V=0
不是
不是
注意:保持静止 和 瞬时速度为0 不同
二.平衡条件
物体处于平衡状态时
它的运动状态V不变
它的加速度a为零
根据牛顿第二定律
F合=0
理论分析:
结论:共点力作用下物体的平衡条件是合力为0,即F合=0
例2 如图,某个物体在F1、F2、F3、F4四个力的作用下处于静止状态,若F4的方向沿逆时针转过60°而保持其大小不变,其余三个力的大小和方向均不变,则此时物体所受到的合力大小为( )
例2 如图,某个物体在F1、F2、F3、F4四个力的作用下处于静止状态,若F4的方向沿逆时针转过60°而保持其大小不变,其余三个力的大小和方向均不变,则此时物体所受到的合力大小为( )
F4
F4’
1200
F4
例2 如图,某个物体在F1、F2、F3、F4四个力的作用下处于静止状态,若F4的方向沿逆时针转过60°而保持其大小不变,其余三个力的大小和方向均不变,则此时物体所受到的合力大小为( )
F4
F4’
1200
F4
例2. 如图,某个物体在F1、F2、F3、F4四个力的作用下处于静止状态,若F4的方向沿逆时针转过60°而保持其大小不变,其余三个力的大小和方向均不变,则此时物体所受到的合力大小为( )
F4
F4’
1200
F4
C
三.解决共点力平衡问题的一般方法
二.平衡条件: F合= 0
1.二力平衡: 两个力等大、反向、共线
书写笔记
2.三力平衡:任意两个力的合力与第三个力等大、反向。
3.多力平衡:
任意一个力与其余各力的合力等大、反向
F1
F2
F3
F4
F5
三.解决共点力平衡问题的一般方法
1.正交分解法
F合=0
X:FX合=0
Y:FY合=0
书写笔记
例3.
例2. 如图,某个物体在F1、F2、F3、F4四个力的作用下处于静止状态,若F4的方向沿逆时针转过60°而保持其大小不变,其余三个力的大小和方向均不变,则此时物体所受到的合力大小为( )
F4
F4’
1200
F4
C
简化为二力平衡
例2. 如图,某个物体在F1、F2、F3、F4四个力的作用下处于静止状态,若F4的方向沿逆时针转过60°而保持其大小不变,其余三个力的大小和方向均不变,则此时物体所受到的合力大小为( )
F4
F4’
1200
F4
C
简化为二力平衡
F合=0
例2. 如图,某个物体在F1、F2、F3、F4四个力的作用下处于静止状态,若F4的方向沿逆时针转过60°而保持其大小不变,其余三个力的大小和方向均不变,则此时物体所受到的合力大小为( )
F4
F4’
1200
F4
C
简化为二力平衡
F合=0
θ
例3.
m
静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.竖直挡板对小球的支持力
mg
N1
N2
x
y
θ
θ
m
θ
例3.
m
静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.竖直挡板对小球的支持力
mg
N1
N2
x
y
θ
X:
N2=N1 sinθ
Y:
N1 cos θ=mg
N1=mg/ cos θ
N2=mg tan θ
θ
例3.
m
静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.竖直挡板对小球的支持力
mg
N1
N2
x
y
θ
X:
N2=N1 sinθ
Y:
N1 cos θ=mg
N1=mg/ cos θ
N2=mg tan θ
θ
例3.
m
静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.竖直挡板对小球的支持力
mg
N1
N2
x
y
θ
X:
N2=N1 sinθ
Y:
N1 cos θ=mg
N1=mg/ cos θ
N2=mg tan θ
解题步骤:
(1)明确研究对象.
(2)受力分析
θ
例3.
m
静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.竖直挡板对小球的支持力
mg
N1
N2
x
y
θ
X:
N2=N1 sinθ
Y:
N1 cos θ=mg
N1=mg/ cos θ
N2=mg tan θ
解题步骤:
(1)明确研究对象.
(2)受力分析
(3) 建立直角坐标系,正交分解.
(4)根据Fx合=0,Fy合=0,列方程求解.
θ
例3.
m
静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.竖直挡板对小球的支持力
mg
N1
N2
x
y
θ
X:
N2=N1 sinθ
Y:
N1 cos θ=mg
N1=mg/ cos θ
N2=mg tan θ
解题步骤:
(1)明确研究对象.
(2)受力分析
(3) 建立直角坐标系,正交分解.
(4)根据Fx合=0,Fy合=0,列方程求解.
θ
m
例3.静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.竖直挡板对小球的支持力
mg
N1
N2
x
y
θ
X:
N2=N1 sinθ
Y:
N1 cos θ=mg
N1=mg/ cos θ
N2=mg tan θ
解题步骤:
(1)明确研究对象.
(2)受力分析
(3)建立直角坐标系,正交分解.
(4)根据Fx合=0,Fy合=0,列方程求解.
θ
m
例4.
θ
m
例3.静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.竖直挡板对小球的支持力
mg
N1
N2
x
y
θ
X:
N2=N1 sinθ
Y:
N1 cos θ=mg
N1=mg/ cos θ
N2=mg tan θ
解题步骤:
(1)明确研究对象.
(2)受力分析.
(3)建立直角坐标系,正交分解.
(4)根据Fx合=0,Fy合=0,列方程求解.
θ
m
例3.静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.竖直挡板对小球的支持力
mg
N1
N2
x
y
θ
X:
N2=N1 sinθ
Y:
N1 cos θ=mg
N1=mg/ cos θ
N2=mg tan θ
解题步骤:
(1)明确研究对象.
(2)受力分析.
(3)建立直角坐标系,正交分解.
(4)根据Fx合=0,Fy合=0,列方程求解.
θ
m
例4.静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.竖直挡板对小球的支持力
G
N1
N2
N1
N2
θ
m
例3.静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.竖直挡板对小球的支持力
mg
N1
N2
X:
N2=N1 sinθ
Y:
N1 cos θ=mg
N1=mg/ cos θ
N2=mg tan θ
θ
m
例4.静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.竖直挡板对小球的支持力
mg
N1
N2
N1
N2
θ
=mg cos θ
=mg sin θ
θ
m
例3.静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.竖直挡板对小球的支持力
mg
N1
N2
X:
N2=N1 sinθ
Y:
N1 cos θ=mg
N1=mg/ cos θ
N2=mg tan θ
N1
N2
θ
=mg/ cos θ
=mg tan θ
三.解决共点力平衡问题的一般方法
1.正交分解法
F合=0
X:FX合=0
Y:FY合=0
书写笔记
2.三角形法
适用于:一切平衡
适用于:三力平衡,且有两力垂直
三.解决共点力平衡问题的一般方法
1.正交分解法
F合=0
X:FX合=0
Y:FY合=0
书写笔记
2.三角形法
适用于:一切平衡
适用于:三力平衡,且有两力垂直
例5.如图,AO,BO,和CO三根绳子能承受的最大拉力相等,0为结 点,BO与竖直方向夹角为300,悬挂物质量为m.
求:OA,OB两根绳子拉力的大小
O
A
B
C
300
例5.如图,AO,BO,和CO三根绳子能承受的最大拉力相等,0为结 点,BO与竖直方向夹角为θ=300 ,悬挂物质量为m.
求:OA,OB两根绳子拉力的大小
O
A
B
C
θ
mg
TOB
TOA
问题1:增大m,那根绳先断?
TOB
TOA
300
问题2:若B点不动,A点上 移,TOA,TOB将怎样变?
一直减小
先减小后增大
θ
m
mg
N1
N2
N1
N2
?
?
缓慢
一直减小
一直增大
θ
m
例3.静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.竖直挡板对小球的支持力
mg
N1
N2
X:
N2=N1 sinθ
Y:
N1 cos θ=mg
N1=mg/ cos θ
N2=mg tan θ
N1
N2
θ
=mg/ cos θ
=mg tan θ
三.解决共点力平衡问题的一般方法
1.正交分解法
F合=0
X:FX合=0
Y:FY合=0
书写笔记
2.三角形法
适用于:一切平衡
适用于:三力平衡,且有两力垂直
θ
m
mg
N1
N2
N1
N2
?
?
缓慢
一直减小
一直增大
例5.如图,AO,BO,和CO三根绳子能承受的最大拉力相等,0为结 点,BO与竖直方向夹角为θ=300 ,悬挂物质量为m.
求:OA,OB两根绳子拉力的大小
O
A
B
C
θ
mg
TOB
TOA
问题1:增大m,那根绳先断?
TOB
TOA
300
问题2:若B点不动,A点上 移,TOA,TOB将怎样变?
一直减小
先减小后增大
动态三角形法,解动态平衡问题
θ
m
mg
N1
N2
N1
N2
缓慢
?
?
一直减小
先减小后增大
三.解决共点力平衡问题的一般方法
1.正交分解法
F合=0
X:FX合=0
Y:FY合=0
书写笔记
2.三角形法
适用于:一切平衡
适用于:三力平衡,且有两力垂直
例5.如图,AO,BO,和CO三根绳子能承受的最大拉力相等,0为结 点,BO与竖直方向夹角为θ=300 ,悬挂物质量为m.
求:OA,OB两根绳子拉力的大小
O
A
B
C
θ
mg
TOB
TOA
问题1:增大m,那根绳先断?
TOB
TOA
300
问题2:若B点不动,A点上 移,TOA,TOB将怎样变?
一直减小
先减小后增大
三角形法,解动态平衡问题
三.解决共点力平衡问题的一般方法
1.正交分解法
F合=0
X:FX合=0
Y:FY合=0
书写笔记
2.三角形法
适用于:一切平衡
适用于:三力平衡,且有两力垂直
三.解决共点力平衡问题的一般方法
1.正交分解法
F合=0
X:FX合=0
Y:FY合=0
书写笔记
2.三角形法
适用于:一切平衡
适用于:三力平衡,且有两力垂直
3、三角形法---解动态平衡问题
例6.如图所示,一个重为G的圆球,被一段细绳挂在竖直光滑墙上,绳与竖直墙的夹角为α,则绳子的拉力和墙壁对球的弹力各是多少?
α
第四章 物体的平衡
4.1 共点力作用下物体的平衡
1.什是共点力?
2.什么是平衡状态?
3.平衡条件是什么?
4.平衡问题的一般解法?
课堂小结
1.什是共点力?
2.什么是平衡状态?
3.平衡条件是什么?
4.平衡问题的一般解法?
课堂小结
1.什是共点力?
2.什么是平衡状态?
3.平衡条件是什么?
4.平衡问题的一般解法?
解决了以下四个问题:
练习1.如图所示,一个重为G的圆球,被一段细绳挂在竖直光滑 墙上,绳与竖直墙的夹角为α,则
( 1 )绳子的拉力T和墙壁对球的弹力N各是多少?
( 2 )若绳子变长,T、N将怎样变化?
α
练习2、在水平路面上用绳子拉一只重100N的箱子,绳子和路面的夹角为37°,如图所示.当绳子的拉力为50N,恰好使箱子匀速移动。
求1.箱子受到的摩擦力
2.箱子和地面间的动摩擦因数.
37o
F
练习2、在水平路面上用绳子拉一只重100N的箱子,绳子和路面的夹角为37°,如图所示.当绳子的拉力为50N,恰好使箱子匀速移动。求:
( 1 )箱子受到的摩擦力
( 2 )箱子和地面间的动摩擦因数.
37o
F
例5.如图,AO,BO,和CO三根绳子能承受的最大拉力相等,0为结 点,BO与竖直方向夹角为θ=300 ,悬挂物质量为m.
求:OA,OB两根绳子拉力的大小
O
A
B
C
θ
mg
TOB
TOA
问题1:增大m,那根绳先断?
TOB
TOA
300
问题2:若B点不动,A点上 移,TOA,TOB将怎样变?
一直减小
先减小后增大
三角形法,解动态平衡问题
拓展:
练习1、在水平路面上用绳子拉一只重100N的箱子,绳子和路面的夹角为37°,如图所示.当绳子的拉力为50N,恰好使箱子匀速移动。求:
( 1 )箱子受到的摩擦力
( 2 )箱子和地面间的动摩擦因数.
37o
F
练习2.如图所示,一个重为G的圆球,被一段细绳挂在竖直光滑 墙上,绳与竖直墙的夹角为α,则
( 1 )绳子的拉力T和墙壁对球的弹力N各是多少?
( 2 )若绳子变长,T、N将怎样变化?
α
练习3.物体A在水平力F1=400N的作用下,沿倾角θ=60°的斜面匀速下滑,如图所示。物体A受的重力G=400N,求:
(1)斜面对物体A的支持力
(2)A与斜面间的动摩擦因数μ.
A
F1
60°
练习1、如图所示,质量为m的物体在恒力F作用下,沿水平天花板向右做匀速直线运动.力F与水平方向的夹角为θ,重力加速度为g.则物体与天花板间的动摩擦因数μ=________.
练习3.如图所示,细绳CO与竖直方向成30°角,A、B两物体用跨过滑轮的细绳相连,已知物体B所受到的重力为100N,地面对物体B的支持力为80N,试求:
(1)物体A所受到的重力;
(2)物体B与地面间的摩擦力;
(3)细绳CO受到的拉力。
同学们,再见!
第四章 物体的平衡
4.1 共点力作用下物体的平衡
1.什么是共点力?
2.什么是平衡状态?
3.平衡条件是什么?
4.平衡问题的一般解法?
一.平衡状态
1.共点力: 如果多个力作用在同一点,或者它们的作用线 相交于一点,这几个力叫做共点力
书写笔记
?
θ
m
例4.静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.挡板对小球的支持力
mg
N1
N2
N1
N2
θ
=mg cos θ
=mg sin θ
例5.如图,AO,BO,和CO三根绳子能承受的最大拉力相等,0为结 点,BO与竖直方向夹角为θ=300 ,悬挂物质量为m.
求:OA,OB两根绳子拉力的大小
O
A
B
C
θ
mg
TOB
TOA
问题1:增大m,那根绳先断?
TOB
TOA
300
问题2:若B点不动,A点缓慢上移,TOA,TOB将怎样变?
一直减小
先减小后增大
三角形法,解动态平衡问题
拓展:
练习1、如图所示,质量为m的物体在恒力F作用下,沿水平天花板向右做匀速直线运动.力F与水平方向的夹角为θ,重力加速度为g.则物体与天花板间的动摩擦因数μ=________.
练习3.如图所示,细绳CO与竖直方向成30°角,A、B两物体用跨过滑轮的细绳相连,已知物体B所受到的重力为100N,地面对物体B的支持力为80N,试求:
(1)物体A所受到的重力;
(2)物体B与地面间的摩擦力;
(3)细绳CO受到的拉力。
一.平衡状态
1.共点力: 如果多个力作用在物体的同一点,或者它们的作用线 相交于一点,这几个力叫做共点力
书写笔记
2.平衡状态:物体处于静止或者匀速直线运动的状态叫做平衡状态。
a=0
3.平衡状态的分类
静态平衡:保持静止
动态平衡:匀速直线、
速度V不变
物体缓慢运动
θ
m
例3.静止在光滑斜面上的小球质量m,求:
1.斜面对小球的支持力 2.竖直挡板对小球的支持力
mg
N1
N2
X:
N2=N1 sinθ
Y:
N1 cos θ=mg
N1=mg/ cos θ
N2=mg tan θ
N1
N2
θ
=mg/ cos θ
=mg tan θ
例5.如图,AO,BO,和CO三根绳子能承受的最大拉力相等,0为结 点,BO与竖直方向夹角为θ=300 ,悬挂物质量为m.
求:OA,OB两根绳子拉力的大小
O
A
B
C
θ
mg
TOB
TOA
问题1:增大m,那根绳先断?
TOB
TOA
300
问题2:若B点不动,A点缓慢上移,TOA,TOB将怎样变?
一直减小
先减小后增大
三角形法,解动态平衡问题
拓展:
θ
m
mg
N1
N2
N1
N2
?
?
缓慢
一直减小
一直增大
θ
m
mg
N1
N2
N1
N2
缓慢
?
?
一直减小
先减小后增大
课堂小结
1.什么是共点力?
2.什么是平衡状态?
3.平衡条件是什么?
4.平衡问题的一般解法?
解决了以下四个问题:
一.平衡状态
1.共点力: 如果多个力作用在物体的同一点,或者它们的作用线 相交于一点,这几个力叫做共点力
书写笔记
2.平衡状态:物体处于静止或者匀速直线运动的状态
a=0
3.平衡状态的分类
静态平衡:保持静止
动态平衡:匀速直线、
速度V不变
物体缓慢运动
二.平衡条件
G
N
G
N
实验验证:
结论:二力平衡时:两个力等大、反向、共线
1.二力平衡
二.平衡条件
G
N
G
N
实验验证:
结论:二力平衡时:两个力等大、反向、共线
1.二力平衡
例5.如图,AO,BO,和CO三根绳子能承受的最大拉力相等,0为结 点,BO与竖直方向夹角为θ=300 ,悬挂物质量为m.
求:OA,OB两根绳子拉力的大小
O
A
B
C
θ
mg
TOB
TOA
问题1:增大m,哪根绳先断?
TOB
TOA
300
问题2:若B点不动,A点缓慢上移,TOA,TOB将怎样变?
一直减小
先减小后增大
三角形法,解动态平衡问题
拓展:
θ
m
mg
N1
N2
N1
N2
?
?
缓慢
一直减小
一直增大
θ
m
mg
N1
N2
N1
N2
缓慢
?
?
一直减小
先减小后增大
同课章节目录
- 第一章 运动的描述
- 1 质点 参考系 空间 时间
- 2 位置变化的描述——位移
- 3 运动快慢与方向的描述——速度
- 4 速度变化快慢的描述——加速度
- 5 匀变速直线运动速度与时间的关系
- 6 匀变速直线运动位移与时间的关系
- 7 对自由落体运动的研究
- 8 匀变速直线运动规律的应用
- 9 测定匀变速直线运动的加速度
- 第二章 力
- 1 力
- 2 重力
- 3 弹力
- 4 摩擦力
- 5 力的合成
- 6 力的分解
- 第三章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿第三定律
- 5 牛顿运动定律的应用
- 6 超重与失重
- 第四章 物体的平衡
- 1 共点力作用下物体的平衡
- 2 共点力平衡条件的应用
- 3 平衡的稳定性(选学)
