人教版八年级数学上册课时练 :13.1.1 轴对称(word版,含答案)
文档属性
| 名称 | 人教版八年级数学上册课时练 :13.1.1 轴对称(word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 308.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-02 10:44:41 | ||
图片预览

文档简介
人教版八年级数学上册课时练
第十三章
轴对称
13.1.1
轴对称
一、单选题
1.如图所示,D是线段AB,BC垂直平分线的交点,若,则的大小是(
).
A.
B.
C.
D.
2.如图,将沿翻折,使其顶点均落在点处,若,则的度数为(
)
A.
B.
C.
D.
3.如图,△ABC中,∠A=20°,沿BE将此三角形对折,又沿BA′再一次对折,点C落在BE上的C′处,此时∠C′DB=74°,则原三角形的∠C的度数为(
)
A.27°
B.59°
C.69°
D.79°
4.下列说法正确的是(
)
A.长方形有且只有一条对称轴
B.垂直于线段的直线就是线段的对称轴
C.角的对称轴是角的平分线
D.角平分线所在的直线是角的对称轴
5.若一个三角形是轴对称图形,则这个三角形一定是(
)
A.等边三角形
B.不等边三角形
C.等腰三角形
D.等腰直角三角形
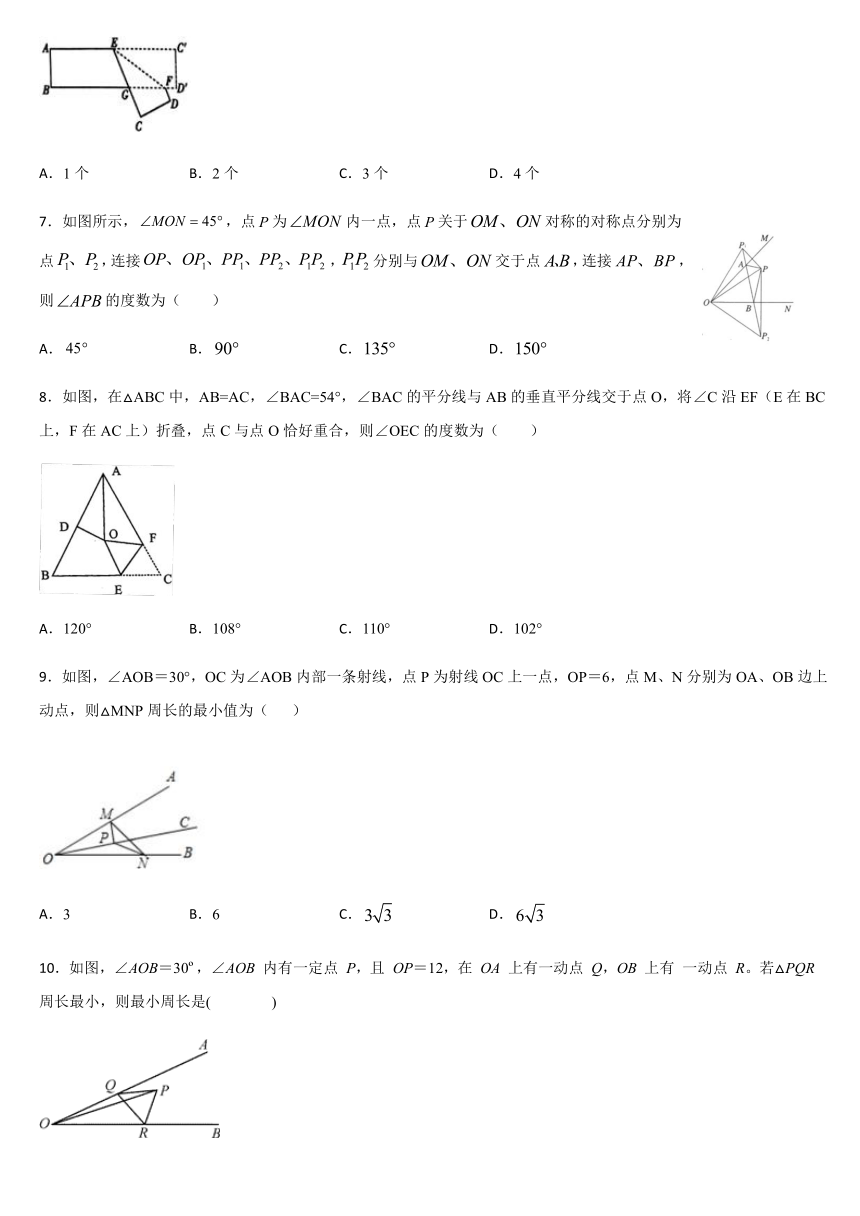
6.把一张对边互相平行的纸条,折成如图所示,是折痕,若,则下列结论正确的有是( )
(1);(2);
(3);(4).
A.1个
B.2个
C.3个
D.4个
7.如图所示,,点为内一点,点关于对称的对称点分别为点,连接,分别与交于点,连接,则的度数为(
)
A.
B.
C.
D.
8.如图,在△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC的度数为(
)
A.120°
B.108°
C.110°
D.102°
9.如图,∠AOB=30°,OC为∠AOB内部一条射线,点P为射线OC上一点,OP=6,点M、N分别为OA、OB边上动点,则△MNP周长的最小值为(
)
A.3
B.6
C.
D.
10.如图,∠AOB=30?,∠AOB
内有一定点
P,且
OP=12,在
OA
上有一动点
Q,OB
上有
一动点
R。若△PQR
周长最小,则最小周长是(
)
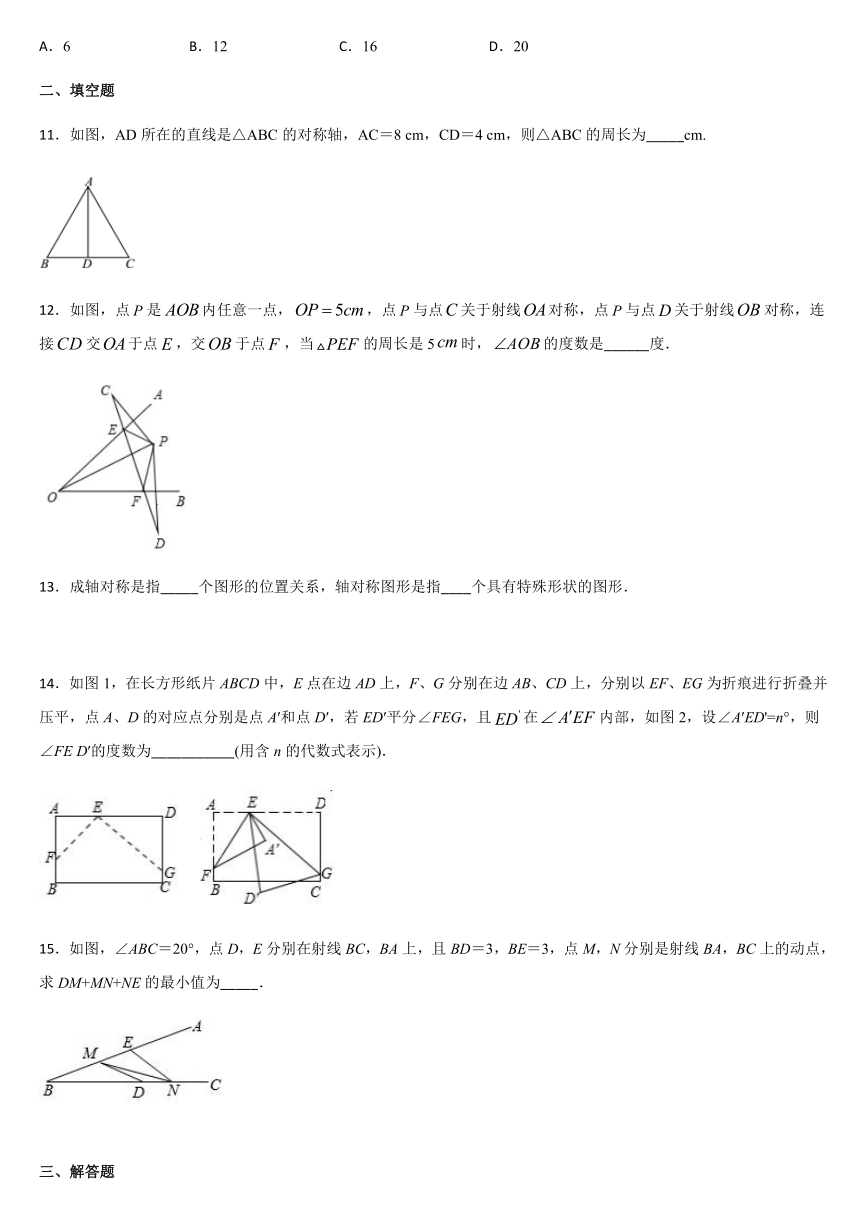
A.6
B.12
C.16
D.20
二、填空题
11.如图,AD所在的直线是△ABC的对称轴,AC=8
cm,CD=4
cm,则△ABC的周长为_____cm.
12.如图,点是内任意一点,,点与点关于射线对称,点与点关于射线对称,连接交于点,交于点,当的周长是5时,的度数是______度.
13.成轴对称是指_____个图形的位置关系,轴对称图形是指____个具有特殊形状的图形.
14.如图1,在长方形纸片ABCD中,E点在边AD上,F、G分别在边AB、CD上,分别以EF、EG为折痕进行折叠并压平,点A、D的对应点分别是点A′和点D′,若ED′平分∠FEG,且在内部,如图2,设∠A′ED'=n°,则∠FE
D′的度数为___________(用含n的代数式表示).
15.如图,∠ABC=20°,点D,E分别在射线BC,BA上,且BD=3,BE=3,点M,N分别是射线BA,BC上的动点,求DM+MN+NE的最小值为_____.
三、解答题
16.在△ABC中,已知∠A=α.
(1)如图1,∠ABC、∠ACB的平分线相交于点D.求∠BDC的大小(用含α的代数式表示);
(2)如图2,若∠ABC的平分线与∠ACE的平分线交于点F,求∠BFC的大小(用含α的代数式表示);
(3)在(2)的条件下,将△FBC以直线BC为对称轴翻折得到△GBC,∠GBC的平分线与∠GCB的平分线交于点M(如图3),求∠BMC的度数(用含α的代数式表示).
17.如图,将△ABC纸片沿DM折叠,使点C落在点的位置,其中点D为AC边上一定点,点M为BC边上一动点,点M与B,C不重合.
(1)若∠A=84°,∠B=61°,则∠=
°;
(2)如图1,当点落在四边形ABMD内时,设∠BM=∠1,∠AD=∠2,探索∠与∠1,∠2之间的数量关系,并说明理由;
(3)在点M运动过程中,折叠图形,若∠=35°,∠BM=53°,求∠AD的度数.
18.定义:在三角形中,把一边的中点到这条边的高线的距离叫做这条边的中垂距.例:如图①,在△ABC中,D为边BC的中点,AE⊥BC于E,则线段DE的长叫做边BC的中垂距.
(1)设三角形一边的中垂距为d(d≥0).若d=0,则这样的三角形一定是
,推断的数学依据是
.
(2)如图②,在△ABC中,∠B=45°,AB=3,BC=8,AD为边BC的中线,求边BC的中垂距.
(3)如图③,在矩形ABCD中,AB=6,AD=4.点E为边CD的中点,连结AE并延长交BC的延长线于点F,连结AC.求△ACF中边AF的中垂距.
19.如图,在△ABC中,AB=AC,D、E是BC边上的点,连接AD,AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,连接D′C,若BD=CD′;
(1)求证:△ABD≌△ACD′;
(2)若∠BAC=120°,求∠DAE的度数.
20.综合与探究
如图,等腰直角中,,,现将该三角形放置在平面直角坐标系中,点坐标为,点坐标为.
(1)过点作轴,求的长及点的坐标;
(2)连接,若为坐标平面内异于点的点,且以、、为顶点的三角形与全等,请直接写出满足条件的点的坐标;
(3)已知,试探究在轴上是否存在点,使是以为腰的等腰三角形?若存在,请直接写出点的坐标;若不存在,请说明理由.
21.如果两个角之差的绝对值等于45°,则称这两个角互为“半余角”,即若|∠α-∠β
|=45°,则称∠α、∠β互为半余角.(注:本题中的角是指大于0°且小于180°的角)
(1)若∠A=80°,则∠A的半余角的度数为 ;
(2)如图1,将一长方形纸片ABCD沿着MN折叠(点M在线段AD上,点N在线段CD上)使点D落在点D′处,若∠AMD′与∠DMN互为“半余角”,求∠DMN的度数;
(3)在(2)的条件下,再将纸片沿着PM折叠(点P在线段BC上),点A、B分别落在点A′、B′处,如图2.若∠AMP比∠DMN大5°,求∠A′MD′的度数.
22.如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B′处,得到折痕EC;将∠AEF对折,点A落在直线EF上的点A′处,得到折痕EN.
(1)若∠BEB′=110°,则∠BEC=
°,∠AEN=
°,∠BEC+∠AEN=
°.
(2)若∠BEB′=m°,则(1)中∠BEC+∠AEN的值是否改变?请说明你的理由.
(3)将∠ECF对折,点E刚好落在F处,且折痕与B′C重合,求∠AEN的度数.(提示,长方形的四个角都是90°)
23.如图,将△ABC
分别沿
AB,AC
翻折得到△ABD
和△AEC,线段
BD
与AE
交于点
F.
(1)若∠ABC=16?,∠ACB=30°,求∠DAE
及∠BFE
的值;
(2)若
BD
与
CE
所在的直线互相垂直,求∠CAB
的度数.
【参考答案】
1.A
2.B
3.D
4.D
5.C
6.C
7.B
8.B
9.B
10.B
11.24
12.30
两
一
14.
15.3.
16.(1)∠BDC=90°+;(2)∠BFC=;(3)∠BMC=90°+.
17.(1)35
(2)2∠C′=∠1+∠2,理由略
(3)17°或123°
18.(1)等腰三角形;线段的垂直平分线上的点到两端的距离相等;(2)1;(3).
19.()证明:∵以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,
∴,
在△ABD和△ACD′中,
∵
,
∴
△ABD≌△ACD′(SSS).
()解:∵≌,
∴,
∴,
∵以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,
∴,
即.
20.(1)4,;(2)或或;(3)或或
21.(1)35°或125°;(2)45°或75°;(3)10°或130°.
22.(1)55,35,90;(2)不改变,理由路;(3)∠AEN=30°
23.(1)42°,108°;(2)135°.
第十三章
轴对称
13.1.1
轴对称
一、单选题
1.如图所示,D是线段AB,BC垂直平分线的交点,若,则的大小是(
).
A.
B.
C.
D.
2.如图,将沿翻折,使其顶点均落在点处,若,则的度数为(
)
A.
B.
C.
D.
3.如图,△ABC中,∠A=20°,沿BE将此三角形对折,又沿BA′再一次对折,点C落在BE上的C′处,此时∠C′DB=74°,则原三角形的∠C的度数为(
)
A.27°
B.59°
C.69°
D.79°
4.下列说法正确的是(
)
A.长方形有且只有一条对称轴
B.垂直于线段的直线就是线段的对称轴
C.角的对称轴是角的平分线
D.角平分线所在的直线是角的对称轴
5.若一个三角形是轴对称图形,则这个三角形一定是(
)
A.等边三角形
B.不等边三角形
C.等腰三角形
D.等腰直角三角形
6.把一张对边互相平行的纸条,折成如图所示,是折痕,若,则下列结论正确的有是( )
(1);(2);
(3);(4).
A.1个
B.2个
C.3个
D.4个
7.如图所示,,点为内一点,点关于对称的对称点分别为点,连接,分别与交于点,连接,则的度数为(
)
A.
B.
C.
D.
8.如图,在△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC的度数为(
)
A.120°
B.108°
C.110°
D.102°
9.如图,∠AOB=30°,OC为∠AOB内部一条射线,点P为射线OC上一点,OP=6,点M、N分别为OA、OB边上动点,则△MNP周长的最小值为(
)
A.3
B.6
C.
D.
10.如图,∠AOB=30?,∠AOB
内有一定点
P,且
OP=12,在
OA
上有一动点
Q,OB
上有
一动点
R。若△PQR
周长最小,则最小周长是(
)
A.6
B.12
C.16
D.20
二、填空题
11.如图,AD所在的直线是△ABC的对称轴,AC=8
cm,CD=4
cm,则△ABC的周长为_____cm.
12.如图,点是内任意一点,,点与点关于射线对称,点与点关于射线对称,连接交于点,交于点,当的周长是5时,的度数是______度.
13.成轴对称是指_____个图形的位置关系,轴对称图形是指____个具有特殊形状的图形.
14.如图1,在长方形纸片ABCD中,E点在边AD上,F、G分别在边AB、CD上,分别以EF、EG为折痕进行折叠并压平,点A、D的对应点分别是点A′和点D′,若ED′平分∠FEG,且在内部,如图2,设∠A′ED'=n°,则∠FE
D′的度数为___________(用含n的代数式表示).
15.如图,∠ABC=20°,点D,E分别在射线BC,BA上,且BD=3,BE=3,点M,N分别是射线BA,BC上的动点,求DM+MN+NE的最小值为_____.
三、解答题
16.在△ABC中,已知∠A=α.
(1)如图1,∠ABC、∠ACB的平分线相交于点D.求∠BDC的大小(用含α的代数式表示);
(2)如图2,若∠ABC的平分线与∠ACE的平分线交于点F,求∠BFC的大小(用含α的代数式表示);
(3)在(2)的条件下,将△FBC以直线BC为对称轴翻折得到△GBC,∠GBC的平分线与∠GCB的平分线交于点M(如图3),求∠BMC的度数(用含α的代数式表示).
17.如图,将△ABC纸片沿DM折叠,使点C落在点的位置,其中点D为AC边上一定点,点M为BC边上一动点,点M与B,C不重合.
(1)若∠A=84°,∠B=61°,则∠=
°;
(2)如图1,当点落在四边形ABMD内时,设∠BM=∠1,∠AD=∠2,探索∠与∠1,∠2之间的数量关系,并说明理由;
(3)在点M运动过程中,折叠图形,若∠=35°,∠BM=53°,求∠AD的度数.
18.定义:在三角形中,把一边的中点到这条边的高线的距离叫做这条边的中垂距.例:如图①,在△ABC中,D为边BC的中点,AE⊥BC于E,则线段DE的长叫做边BC的中垂距.
(1)设三角形一边的中垂距为d(d≥0).若d=0,则这样的三角形一定是
,推断的数学依据是
.
(2)如图②,在△ABC中,∠B=45°,AB=3,BC=8,AD为边BC的中线,求边BC的中垂距.
(3)如图③,在矩形ABCD中,AB=6,AD=4.点E为边CD的中点,连结AE并延长交BC的延长线于点F,连结AC.求△ACF中边AF的中垂距.
19.如图,在△ABC中,AB=AC,D、E是BC边上的点,连接AD,AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,连接D′C,若BD=CD′;
(1)求证:△ABD≌△ACD′;
(2)若∠BAC=120°,求∠DAE的度数.
20.综合与探究
如图,等腰直角中,,,现将该三角形放置在平面直角坐标系中,点坐标为,点坐标为.
(1)过点作轴,求的长及点的坐标;
(2)连接,若为坐标平面内异于点的点,且以、、为顶点的三角形与全等,请直接写出满足条件的点的坐标;
(3)已知,试探究在轴上是否存在点,使是以为腰的等腰三角形?若存在,请直接写出点的坐标;若不存在,请说明理由.
21.如果两个角之差的绝对值等于45°,则称这两个角互为“半余角”,即若|∠α-∠β
|=45°,则称∠α、∠β互为半余角.(注:本题中的角是指大于0°且小于180°的角)
(1)若∠A=80°,则∠A的半余角的度数为 ;
(2)如图1,将一长方形纸片ABCD沿着MN折叠(点M在线段AD上,点N在线段CD上)使点D落在点D′处,若∠AMD′与∠DMN互为“半余角”,求∠DMN的度数;
(3)在(2)的条件下,再将纸片沿着PM折叠(点P在线段BC上),点A、B分别落在点A′、B′处,如图2.若∠AMP比∠DMN大5°,求∠A′MD′的度数.
22.如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B′处,得到折痕EC;将∠AEF对折,点A落在直线EF上的点A′处,得到折痕EN.
(1)若∠BEB′=110°,则∠BEC=
°,∠AEN=
°,∠BEC+∠AEN=
°.
(2)若∠BEB′=m°,则(1)中∠BEC+∠AEN的值是否改变?请说明你的理由.
(3)将∠ECF对折,点E刚好落在F处,且折痕与B′C重合,求∠AEN的度数.(提示,长方形的四个角都是90°)
23.如图,将△ABC
分别沿
AB,AC
翻折得到△ABD
和△AEC,线段
BD
与AE
交于点
F.
(1)若∠ABC=16?,∠ACB=30°,求∠DAE
及∠BFE
的值;
(2)若
BD
与
CE
所在的直线互相垂直,求∠CAB
的度数.
【参考答案】
1.A
2.B
3.D
4.D
5.C
6.C
7.B
8.B
9.B
10.B
11.24
12.30
两
一
14.
15.3.
16.(1)∠BDC=90°+;(2)∠BFC=;(3)∠BMC=90°+.
17.(1)35
(2)2∠C′=∠1+∠2,理由略
(3)17°或123°
18.(1)等腰三角形;线段的垂直平分线上的点到两端的距离相等;(2)1;(3).
19.()证明:∵以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,
∴,
在△ABD和△ACD′中,
∵
,
∴
△ABD≌△ACD′(SSS).
()解:∵≌,
∴,
∴,
∵以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,
∴,
即.
20.(1)4,;(2)或或;(3)或或
21.(1)35°或125°;(2)45°或75°;(3)10°或130°.
22.(1)55,35,90;(2)不改变,理由路;(3)∠AEN=30°
23.(1)42°,108°;(2)135°.
