人教版数学七年级上册2..2整式的加减课件(15张)
文档属性
| 名称 | 人教版数学七年级上册2..2整式的加减课件(15张) |  | |
| 格式 | pptx | ||
| 文件大小 | 624.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-04 17:50:34 | ||
图片预览






文档简介
整式的加减
新知引入
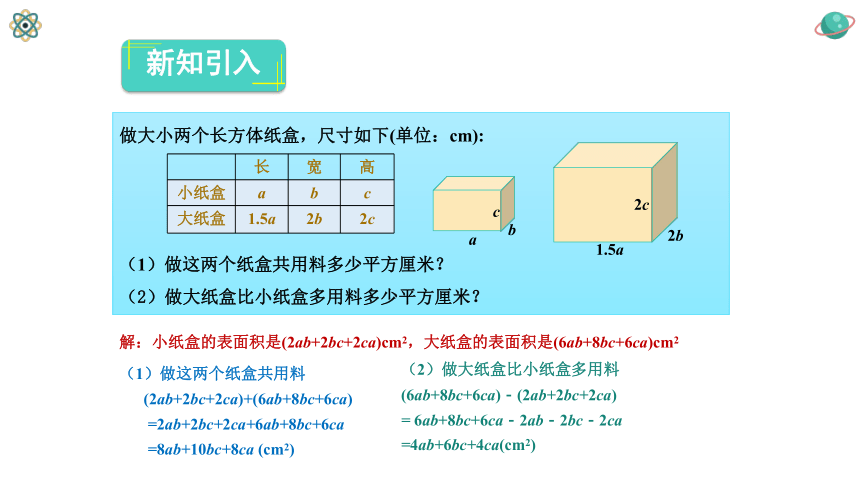
做大小两个长方体纸盒,尺寸如下(单位:cm):
(1)做这两个纸盒共用料多少平方厘米?
(2)做大纸盒比小纸盒多用料多少平方厘米?
长
宽
高
小纸盒
a
b
c
大纸盒
1.5a
2b
2c
a
b
c
1.5a
2b
2c
解:小纸盒的表面积是(2ab+2bc+2ca)cm2,大纸盒的表面积是(6ab+8bc+6ca)cm2
(1)做这两个纸盒共用料
(2ab+2bc+2ca)+(6ab+8bc+6ca)
=2ab+2bc+2ca+6ab+8bc+6ca
=8ab+10bc+8ca (cm2)
(2)做大纸盒比小纸盒多用料(6ab+8bc+6ca)-(2ab+2bc+2ca)
= 6ab+8bc+6ca-2ab-2bc-2ca =4ab+6bc+4ca(cm2)
新知讲解
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
通过上面的学习,你能得到整式加减的运算法则吗?
整式加减实际上就是: 去括号、合并同类项.
整式的加减
1
新知应用
例1.计算:
(1)(2a-3b)+(5a+4b);(2)(8a-7b)-(4a-5b)
解: (1)(2a-3b)+(5a+4b)
=2a-3b+5a+4b
=7a+b
去括号
合并同类项
=8a-7b-4a+5b
=4a-2b
(2)(8a-7b)-(4a-5b)
去括号
合并同类项
新知应用
例2.已知A=x2-2x+1,B=2x2-5,C= x2-5x-3,求2A+B-4C.
解: 2A+B-4C
=2(x2-2x+1)+(2x2-5)-4( x2-5x-3)
=2x2-4x+2+ 2x2-5-2x2+20x+12
= 2x2+16x+9
【变式1】一个多项式与x2-2x+1的和是3x-2,则这个多项式为( )
A.x2-5x+3 B.-x2+x-1
C.-x2+5x-3 D.x2-5x-13
新知演练
C
【变式2】如果A是x的三次多项式,B是x的五次多项式,那么A-B是( )
A.三次多项式 B.二次多项式
C.八次多项式 D.五次多项式
新知演练
D
【变式3】若mn=m+3,则2mn+3m-5mn+10=_____.
新知演练
1
提示:2mn+3m-5mn+10=2(m+3)+3m-5(m+3)+10=1.
当 时,
例3.求 的值,其中 .
新知应用
先将式子化简,再代入数值进行计算.
解:
原式
→去括号
→合并同类项
﹜
将式子化简
新知演练
【变式1】化简求值: a-2(a- b2)-( a+ b2)+1,
其中a=2,b=- .
解:原式= a-2a+ b2- a- b2+1
=-3a+ b2+1,
当a=2,b=- 时,
原式=-3×2+ × (- )2+1
=-6+ +1
=-4 .
【变式2】
新知演练
先化简再求值:4x2y-[6xy-3(4xy-2)-x2y]+1,
其中x=2,y=- .
当x=2,y=- 时,
原式=5×22×(- )+6×2×(- )-5
=-21.
解:原式=4x2y-[6xy-12xy+6-x2y]+1
=4x2y-6xy+12xy-6+x2y+1
=5x2y+6xy-5
1. 已知代数式 的值与x的取值无关,
求代数式 的值.
拓展提升
解:原式
由题意可知:4-2b=0 ,a+7=0 ,
∴ a=-7,b=2 ,
∴原式
=-49-8+24 .
2. 有这样一道题“当a=2,b=-2时,求多项式3a3b3- a2b+b-(4a3b3- a2b-b2)+(a3b3+ a2b)-2b2+3的值”,马小虎做题时把a=2错抄成a=-2,王小真没抄错题,但他们做出的结果却都一样,你知道这是怎么回事吗?说明理由.
解:将原多项式化简后,得-b2+b+3.
因为这个式子的值与a的取值无关,所以即使把a抄错,最后的结果都会一样.
拓展提升
课堂总结
求和差
化简求值
整式的加减
1.根据题意,列出算式
2.去括号,合并同类项
1.去括号
2.合并同类项
3.代入求值
方法
步骤
谢谢聆听
新知引入
做大小两个长方体纸盒,尺寸如下(单位:cm):
(1)做这两个纸盒共用料多少平方厘米?
(2)做大纸盒比小纸盒多用料多少平方厘米?
长
宽
高
小纸盒
a
b
c
大纸盒
1.5a
2b
2c
a
b
c
1.5a
2b
2c
解:小纸盒的表面积是(2ab+2bc+2ca)cm2,大纸盒的表面积是(6ab+8bc+6ca)cm2
(1)做这两个纸盒共用料
(2ab+2bc+2ca)+(6ab+8bc+6ca)
=2ab+2bc+2ca+6ab+8bc+6ca
=8ab+10bc+8ca (cm2)
(2)做大纸盒比小纸盒多用料(6ab+8bc+6ca)-(2ab+2bc+2ca)
= 6ab+8bc+6ca-2ab-2bc-2ca =4ab+6bc+4ca(cm2)
新知讲解
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
通过上面的学习,你能得到整式加减的运算法则吗?
整式加减实际上就是: 去括号、合并同类项.
整式的加减
1
新知应用
例1.计算:
(1)(2a-3b)+(5a+4b);(2)(8a-7b)-(4a-5b)
解: (1)(2a-3b)+(5a+4b)
=2a-3b+5a+4b
=7a+b
去括号
合并同类项
=8a-7b-4a+5b
=4a-2b
(2)(8a-7b)-(4a-5b)
去括号
合并同类项
新知应用
例2.已知A=x2-2x+1,B=2x2-5,C= x2-5x-3,求2A+B-4C.
解: 2A+B-4C
=2(x2-2x+1)+(2x2-5)-4( x2-5x-3)
=2x2-4x+2+ 2x2-5-2x2+20x+12
= 2x2+16x+9
【变式1】一个多项式与x2-2x+1的和是3x-2,则这个多项式为( )
A.x2-5x+3 B.-x2+x-1
C.-x2+5x-3 D.x2-5x-13
新知演练
C
【变式2】如果A是x的三次多项式,B是x的五次多项式,那么A-B是( )
A.三次多项式 B.二次多项式
C.八次多项式 D.五次多项式
新知演练
D
【变式3】若mn=m+3,则2mn+3m-5mn+10=_____.
新知演练
1
提示:2mn+3m-5mn+10=2(m+3)+3m-5(m+3)+10=1.
当 时,
例3.求 的值,其中 .
新知应用
先将式子化简,再代入数值进行计算.
解:
原式
→去括号
→合并同类项
﹜
将式子化简
新知演练
【变式1】化简求值: a-2(a- b2)-( a+ b2)+1,
其中a=2,b=- .
解:原式= a-2a+ b2- a- b2+1
=-3a+ b2+1,
当a=2,b=- 时,
原式=-3×2+ × (- )2+1
=-6+ +1
=-4 .
【变式2】
新知演练
先化简再求值:4x2y-[6xy-3(4xy-2)-x2y]+1,
其中x=2,y=- .
当x=2,y=- 时,
原式=5×22×(- )+6×2×(- )-5
=-21.
解:原式=4x2y-[6xy-12xy+6-x2y]+1
=4x2y-6xy+12xy-6+x2y+1
=5x2y+6xy-5
1. 已知代数式 的值与x的取值无关,
求代数式 的值.
拓展提升
解:原式
由题意可知:4-2b=0 ,a+7=0 ,
∴ a=-7,b=2 ,
∴原式
=-49-8+24 .
2. 有这样一道题“当a=2,b=-2时,求多项式3a3b3- a2b+b-(4a3b3- a2b-b2)+(a3b3+ a2b)-2b2+3的值”,马小虎做题时把a=2错抄成a=-2,王小真没抄错题,但他们做出的结果却都一样,你知道这是怎么回事吗?说明理由.
解:将原多项式化简后,得-b2+b+3.
因为这个式子的值与a的取值无关,所以即使把a抄错,最后的结果都会一样.
拓展提升
课堂总结
求和差
化简求值
整式的加减
1.根据题意,列出算式
2.去括号,合并同类项
1.去括号
2.合并同类项
3.代入求值
方法
步骤
谢谢聆听
