圆周角
图片预览

文档简介
25.4圆周角(2课时)
一、教学目标:
1.知道什么样的角是圆周角
2.了解圆周角和圆心角的关系,直径所对的圆周角的特征
3.能应用圆心角和圆周角的关系、直径所对的圆周角的特征解决相关问题
4.通过对圆心角和圆周角关系的探索,培养学生运用已有知识,进行实验、猜想、论证,从而得到新知。进一步体会分类讨论的思想。
二、教学重难点:
教学重点:
1、了解圆周角和圆心角的关系,直径所对的圆周角的特征
2、能应用圆心角和圆周角的关系、直径所对的圆周角的特征解决相关问题
教学难点:对圆心角和圆周角关系的探索,分类思想的应用。
三、教学过程:
(一)情境导入
如下图,同学们能找到圆心角吗?它具有什么样的特征?(顶点在圆心,两边与圆相交的角叫做圆心角),今天我们要学习圆中的另一种特殊的角,它的名称叫做圆周角。
如下图,同学们能找到圆心角吗?它具有什么样的特征?(顶点在圆心,两边与圆相交的角叫做圆心角),今天我们要学习圆中的另一种特殊的角,它的名称叫做圆周角。
(二)实践与探索1:圆周角
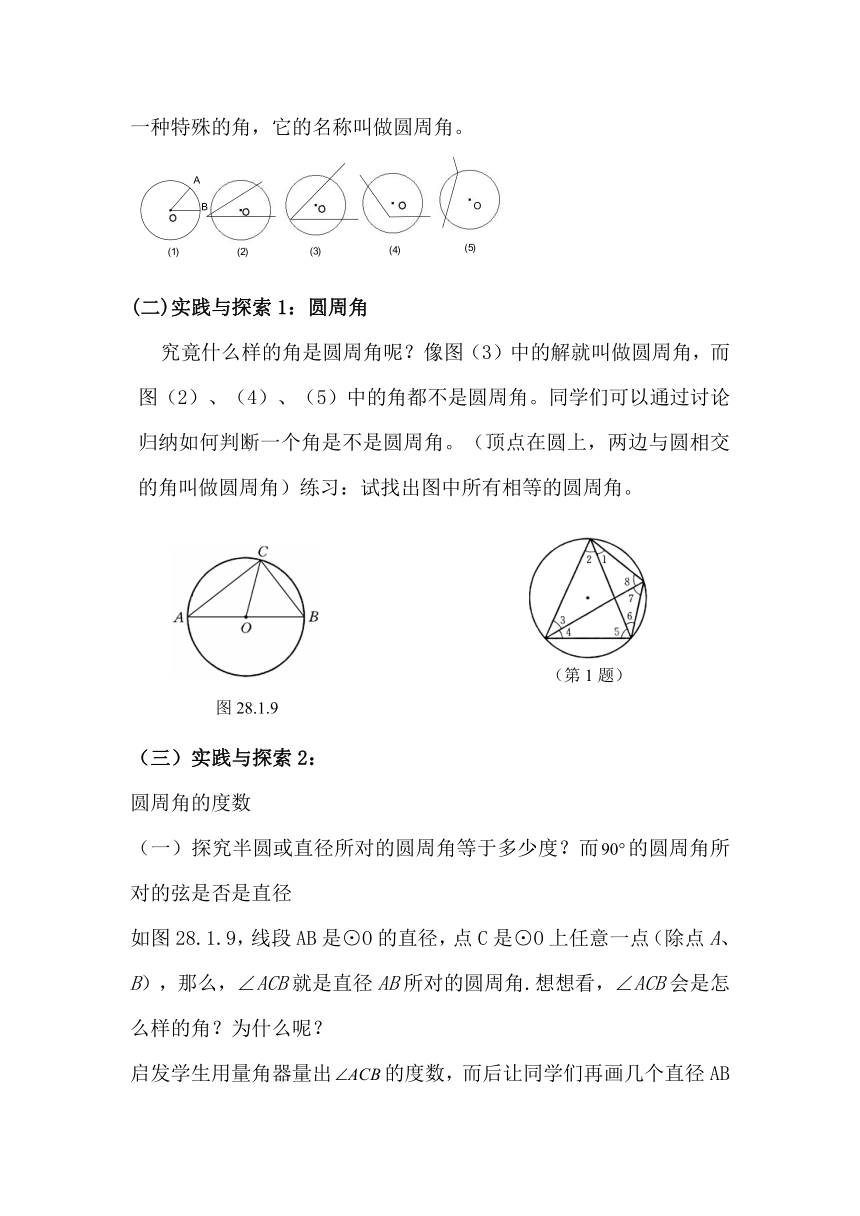
究竟什么样的角是圆周角呢?像图(3)中的解就叫做圆周角,而图(2)、(4)、(5)中的角都不是圆周角。同学们可以通过讨论归纳如何判断一个角是不是圆周角。(顶点在圆上,两边与圆相交的角叫做圆周角)练习:试找出图中所有相等的圆周角。
(三)实践与探索2:
圆周角的度数
(一)探究半圆或直径所对的圆周角等于多少度?而的圆周角所对的弦是否是直径
如图28.1.9,线段AB是⊙O的直径,点C是⊙O上任意一点(除点A、B),那么,∠ACB就是直径AB所对的圆周角.想想看,∠ACB会是怎么样的角?为什么呢?
启发学生用量角器量出的度数,而后让同学们再画几个直径AB所对的圆周角,并测量出它们的度数,通过测量,同学们感性认识到直径所对的圆周角等于(或直角),进而给出严谨的说明。
证明:因为OA=OB=OC,所以△AOC、△BOC都是等腰三角形,所以∠OAC=∠OCA,∠OBC=∠OCB. 又∠OAC+∠OBC+∠ACB=180°,所以∠ACB=∠OCA+∠OCB==90°.因此,不管点C在⊙O上何处(除点A、B),∠ACB总等于90°,即半圆或直径所对的圆周角都相等,都等于90°(直角)。反过来也是成立的,即90°的圆周角所对的弦是圆的直径。
(二)探究同一条弧所对的圆周角和圆心角的关系
1、分别量一量图28.1.10中弧AB所对的两个圆周角的度数比较一下. 再变动点C在圆周上的位置,看看圆周角的度数有没有变化. 你发现其中有什么规律吗?
(2) 分别量出图28.1.10中弧AB所对的圆周角和圆心角的度数,比较一下,你发现什么?
我们可以发现,圆周角的度数没有变化. 并且圆周角的度数恰好为同弧所对的圆心角的度数的一半。
由上述操作可以猜想:在一个圆中,一条弧所对的任意一个圆周角的大小都等于该弧所对的圆心角的一半。
为了验证这个猜想,如图28.1.11所示,可将圆对折,使折痕经过圆心O和圆周角的顶点C,这时可能出现三种情况:(1) 折痕是圆周角的一条边,(2) 折痕在圆周角的内部,(3) 折痕在圆周角的外部。
四、例题讲解:
如图,如图28.1.12,AB是⊙O的直径,∠A=80°.求∠ABC的度数.
五、课后小结
本节课我们一同探究了同圆或等圆中,一条弧所对的圆周角等于这条弧所对的圆心角的一半;由这个结论进一步得到:同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半; 相等的圆周角所对的弧相等;半圆或直径所对的圆周角都相等,都等于90°(直角)。90°(直角)的圆周角所对的弦是圆的直径等结论。
六、作业布置:课本29页练习1、2、3、4、5题
七、课后小结:
一、教学目标:
1.知道什么样的角是圆周角
2.了解圆周角和圆心角的关系,直径所对的圆周角的特征
3.能应用圆心角和圆周角的关系、直径所对的圆周角的特征解决相关问题
4.通过对圆心角和圆周角关系的探索,培养学生运用已有知识,进行实验、猜想、论证,从而得到新知。进一步体会分类讨论的思想。
二、教学重难点:
教学重点:
1、了解圆周角和圆心角的关系,直径所对的圆周角的特征
2、能应用圆心角和圆周角的关系、直径所对的圆周角的特征解决相关问题
教学难点:对圆心角和圆周角关系的探索,分类思想的应用。
三、教学过程:
(一)情境导入
如下图,同学们能找到圆心角吗?它具有什么样的特征?(顶点在圆心,两边与圆相交的角叫做圆心角),今天我们要学习圆中的另一种特殊的角,它的名称叫做圆周角。
如下图,同学们能找到圆心角吗?它具有什么样的特征?(顶点在圆心,两边与圆相交的角叫做圆心角),今天我们要学习圆中的另一种特殊的角,它的名称叫做圆周角。
(二)实践与探索1:圆周角
究竟什么样的角是圆周角呢?像图(3)中的解就叫做圆周角,而图(2)、(4)、(5)中的角都不是圆周角。同学们可以通过讨论归纳如何判断一个角是不是圆周角。(顶点在圆上,两边与圆相交的角叫做圆周角)练习:试找出图中所有相等的圆周角。
(三)实践与探索2:
圆周角的度数
(一)探究半圆或直径所对的圆周角等于多少度?而的圆周角所对的弦是否是直径
如图28.1.9,线段AB是⊙O的直径,点C是⊙O上任意一点(除点A、B),那么,∠ACB就是直径AB所对的圆周角.想想看,∠ACB会是怎么样的角?为什么呢?
启发学生用量角器量出的度数,而后让同学们再画几个直径AB所对的圆周角,并测量出它们的度数,通过测量,同学们感性认识到直径所对的圆周角等于(或直角),进而给出严谨的说明。
证明:因为OA=OB=OC,所以△AOC、△BOC都是等腰三角形,所以∠OAC=∠OCA,∠OBC=∠OCB. 又∠OAC+∠OBC+∠ACB=180°,所以∠ACB=∠OCA+∠OCB==90°.因此,不管点C在⊙O上何处(除点A、B),∠ACB总等于90°,即半圆或直径所对的圆周角都相等,都等于90°(直角)。反过来也是成立的,即90°的圆周角所对的弦是圆的直径。
(二)探究同一条弧所对的圆周角和圆心角的关系
1、分别量一量图28.1.10中弧AB所对的两个圆周角的度数比较一下. 再变动点C在圆周上的位置,看看圆周角的度数有没有变化. 你发现其中有什么规律吗?
(2) 分别量出图28.1.10中弧AB所对的圆周角和圆心角的度数,比较一下,你发现什么?
我们可以发现,圆周角的度数没有变化. 并且圆周角的度数恰好为同弧所对的圆心角的度数的一半。
由上述操作可以猜想:在一个圆中,一条弧所对的任意一个圆周角的大小都等于该弧所对的圆心角的一半。
为了验证这个猜想,如图28.1.11所示,可将圆对折,使折痕经过圆心O和圆周角的顶点C,这时可能出现三种情况:(1) 折痕是圆周角的一条边,(2) 折痕在圆周角的内部,(3) 折痕在圆周角的外部。
四、例题讲解:
如图,如图28.1.12,AB是⊙O的直径,∠A=80°.求∠ABC的度数.
五、课后小结
本节课我们一同探究了同圆或等圆中,一条弧所对的圆周角等于这条弧所对的圆心角的一半;由这个结论进一步得到:同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半; 相等的圆周角所对的弧相等;半圆或直径所对的圆周角都相等,都等于90°(直角)。90°(直角)的圆周角所对的弦是圆的直径等结论。
六、作业布置:课本29页练习1、2、3、4、5题
七、课后小结:
