《2.2.1不等式及其性质》第1课时课件(26张PPT)
文档属性
| 名称 | 《2.2.1不等式及其性质》第1课时课件(26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 209.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-03 21:42:50 | ||
图片预览








文档简介
2.2.1 不等式及其性质
第1课时
问题1 阅读课本第58~61页,回答下列问题:
整体概览
(1)本节将要研究不等式的性质及其证法.(2)起点是初中所学的不等式的性质,目标是掌握不等式5个性质与2个推论,掌握用配方法、作差法、综合法证明不等式.提升逻辑推理素养.
(1)本节将要研究哪类问题?
(2)本节研究的起点是什么?目标是什么?
情境与问题
你见过下图中的高速公路指示牌吗?左边的指示牌是指对应的车道只能供小客车行驶,而且小客车的速率v1(单位:km/h,下同)应该满足
100≤v1≤120;
右边的指示牌是指对应的车道可供客车和货车行驶,而且车的速率v2应该满足_______________.
60≤v2≤100
新知探究
在现实世界里,量与量之间的不等关系是普遍的,不等式是刻画不等关系的工具,我们用数学符号“≠”“>”“<”“≥”“≤”连接两个数或代数式,以表示它们之间的不等关系,含有这些不等号的式子,称为不等式.
上述不等式符号中,要特别注意“≥”“≤”.事实上,住意给定两个实数a,b,那么
a<b或a=b
a≥b?a>b或a=b; a≤b?____________.
新知探究
【想一想】5≥3,2≥2,2≤2这三个命题都是真命题吗?
根据不等号的含义可知:三个命题都是真命题.
新知探究
问题1 怎样理解两个实数之间的大小呢?
结论:a-b<0?a<b,b=0?a=b,a-b>0?a>b.
新知探究
问题2 初中学过的不等式有哪些性质呢?
不等式的三个性质:
性质1 如果a>b,那么a+c>b+c.
性质2 如果a>b,c>0,那么ac>bc.
性质3 如果a>b,c<0,那么ac<bc.
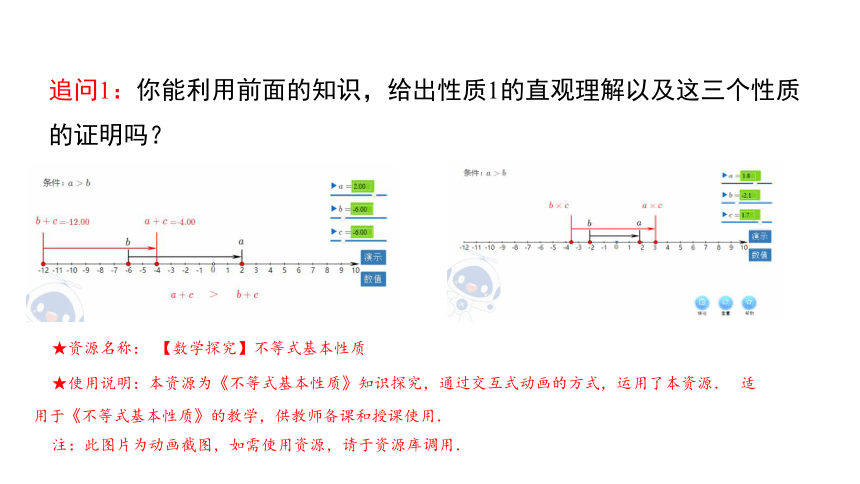
追问1:你能利用前面的知识,给出性质1的直观理解以及这三个性质的证明吗?
新知探究
★资源名称: 【数学探究】不等式基本性质
★使用说明:本资源为《不等式基本性质》知识探究,通过交互式动画的方式,运用了本资源. 适用于《不等式基本性质》的教学,供教师备课和授课使用.
注:此图片为动画截图,如需使用资源,请于资源库调用.
追问1:你能利用前面的知识,给出性质1的直观理解以及这三个性质的证明吗?
新知探究
性质1:因为(a+c)-(b+c)=a+c-b-c=a-b,
又因为a>b,所以a-b>0,从而(a+c)-(b+c)>0.
因此a+c>b+c.
性质2:因为ac-bc=(a-b)c,
又因为a>b,所以a-b>0,而c>0,因此(a-b)c>0,
因此ac-bc>0,即ac>bc.
追问2:你会用充分条件、必要条件来描述不等式的性质吗?试用“充分不必要”“必要不充分”“充要”填空:
新知探究
(1)a>b是a+c>b+c的_______条件;
(2)如果c>0,则a>b是ac>bc的_______条件;
(3)如果c<0,则a>b是ac<bc的_______条件.
充要
充要
充要
追问3:不等式还有哪些性质呢?
新知探究
性质4 如果a>b,b>c,那么a>c.(通常称为不等关系的传递性)
证明:因为a-c=(a-b)+(b-c),
又因为a>b,所以a-b>0;
且b>c,所以b-c>0,因此(a-b)+(b-c)>0,
从而a-c>0,即a>c.
性质5 a>b?b<a.
这只要利用a-b=-(b-a)就可以证明.
追问3:不等式还有哪些性质呢?
新知探究
强调:值得注意的是,上述不等式性质对任意满足条件的实数都成立,因此我们可以用任意满足条件的式子去代替其中的字母.
新知探究
问题3 利用前面不等式的性质,我们还可以得到关于不等式的哪些结论?
推论1 如果a+b>c,那么a>c-b.
证明 a+b>c?a+b+(-b)>c+(-b)?a>c-b.
推论1表明,不等式中的任意一项都可以把它的符号变成相反的符号后,从不等式的一边移到另一边.推论1通常称为不等式的移项法则.
新知探究
问题3 利用前面不等式的性质,我们还可以得到关于不等式的哪些结论?
推论2 如果a>b,c>d,那么a+c>b+d.
证明 根据性质1有a>b?a+c>b+c,c>d ?b+c>b+d,
再根据性质4可知a+c>b+d.
新知探究
问题3 利用前面不等式的性质,我们还可以得到关于不等式的哪些结论?
我们把a>b和c>d(或a<b和c<d)这类不等号方向相同的不等式,称为同向不等式.推论2说明,两个同向不等式的两边分别相加,所得到的不等式与原不等式同向.很明显,推论2可以推广为更一般的结论:有限个同向不等式的两边分别相加,所得到的不等式与原不等式同向.
新知探究
例1 (1)比较x2-x和x-2的大小.
(2)已知a,b为正数,且a≠b,比较a3+b3与a2b+ab2的大小.
(1)因为(x2-x)-(x-2)=x2-2x+2=(x-1)2+1,
又因为(x-1)2≥0,所以(x-1)2+1≥1>0,
从而(x2-x)-(x-2)>0,因此x2-x>x-2.
新知探究
例1 (1)比较x2-x和x-2的大小.
(2)已知a,b为正数,且a≠b,比较a3+b3与a2b+ab2的大小.
(2)(a3+b3)-(a2b+ab2)=a3+b3-a2b-ab2
=a2(a-b)-b2(a-b)=(a-b)(a2-b2)
=(a-b)2(a+b).
∵a>0,b>0,且a≠b,
∴(a-b)2>0,a+b>0.
∴(a3+b3)-(a2b+ab2)>0,即a3+b3>a2b+ab2.
新知探究
方法总结:通过比较两式之差的符号来判断两式的大小,这种方法通常称为作差法.作差法的步骤:
(1)作差:对要比较大小的两个代数式作差.
(2)变形:对差进行变形(因式分解或者配方等).
(3)判断差的符号:结合变形的结果及题设条件判断差的符号.
(4)作出结论.
新知探究
其思维过程是作差→变形→判断符号→作出结论.当不能直接得到正或负的结论时,还要考虑通过分类讨论来确定.
新知探究
例2 设a≥b>0,求证:3a3+2b3≥3a2b+2ab2.
解:3a3+2b3-(3a2b+2ab2)=3a2(a-b)+2b2(b-a)
=(3a2-2b2)(a-b).
因为a≥b>0,所以a-b≥0,3a2-2b2>0,
从而(3a2-2b2)(a-b)≥0,
所以3a3+2b3≥3a2b+2ab2.
新知探究
方法总结:(1)简单不等式的证明可直接由已知条件并利用不等式的性质,通过对不等式变形得证.
(2)对于不等号两边都比较复杂的式子,直接利用不等式的性质不易得证,可考虑将不等式的两边作差,然后进行变形,根据条件确定每一个因式(式子)的符号,利用符号法则判断最终的符号,完成证明.这种证明方法常说成是比较法.
新知探究
例3 (1)已知a>b,c<d,求证:a-c>b-d;
(2)已知a>b,ab>0,求证: .
证明:(1)因为a>b,c<d,所以a>b,-c>-d,
根据推论2,得a-c>b-d.
(2)因为ab>0,所以 >0,
又因为a>b,所以a· >b· ,
即 ,因此 .
新知探究
方法总结:从已知条件出发,综合利用各种结果,经过逐步推导最后得到结论的方法,在数学中通常称为综合法.本例与前面的推论所使用的方法都是综合法.综合法中,最重要的推理形式为p?q,其中p是已知或者已经得出的结论,所以综合法的实质就是不断寻找必然成立的结论.在证明不等式时,当然也可直接利用已经证明过的不等式性质等.
归纳小结
回顾本节课,你有什么收获?
(1)什么叫不等式?
(2)如何比较两个实数的大小?
(3)不等式的性质有哪些?
(4)不等式的性质有哪些推论?
(5)本节课学了哪些证明不等式的方法?
作业:教科书P63练习B 1、2、3.
作业布置
再见
第1课时
问题1 阅读课本第58~61页,回答下列问题:
整体概览
(1)本节将要研究不等式的性质及其证法.(2)起点是初中所学的不等式的性质,目标是掌握不等式5个性质与2个推论,掌握用配方法、作差法、综合法证明不等式.提升逻辑推理素养.
(1)本节将要研究哪类问题?
(2)本节研究的起点是什么?目标是什么?
情境与问题
你见过下图中的高速公路指示牌吗?左边的指示牌是指对应的车道只能供小客车行驶,而且小客车的速率v1(单位:km/h,下同)应该满足
100≤v1≤120;
右边的指示牌是指对应的车道可供客车和货车行驶,而且车的速率v2应该满足_______________.
60≤v2≤100
新知探究
在现实世界里,量与量之间的不等关系是普遍的,不等式是刻画不等关系的工具,我们用数学符号“≠”“>”“<”“≥”“≤”连接两个数或代数式,以表示它们之间的不等关系,含有这些不等号的式子,称为不等式.
上述不等式符号中,要特别注意“≥”“≤”.事实上,住意给定两个实数a,b,那么
a<b或a=b
a≥b?a>b或a=b; a≤b?____________.
新知探究
【想一想】5≥3,2≥2,2≤2这三个命题都是真命题吗?
根据不等号的含义可知:三个命题都是真命题.
新知探究
问题1 怎样理解两个实数之间的大小呢?
结论:a-b<0?a<b,b=0?a=b,a-b>0?a>b.
新知探究
问题2 初中学过的不等式有哪些性质呢?
不等式的三个性质:
性质1 如果a>b,那么a+c>b+c.
性质2 如果a>b,c>0,那么ac>bc.
性质3 如果a>b,c<0,那么ac<bc.
追问1:你能利用前面的知识,给出性质1的直观理解以及这三个性质的证明吗?
新知探究
★资源名称: 【数学探究】不等式基本性质
★使用说明:本资源为《不等式基本性质》知识探究,通过交互式动画的方式,运用了本资源. 适用于《不等式基本性质》的教学,供教师备课和授课使用.
注:此图片为动画截图,如需使用资源,请于资源库调用.
追问1:你能利用前面的知识,给出性质1的直观理解以及这三个性质的证明吗?
新知探究
性质1:因为(a+c)-(b+c)=a+c-b-c=a-b,
又因为a>b,所以a-b>0,从而(a+c)-(b+c)>0.
因此a+c>b+c.
性质2:因为ac-bc=(a-b)c,
又因为a>b,所以a-b>0,而c>0,因此(a-b)c>0,
因此ac-bc>0,即ac>bc.
追问2:你会用充分条件、必要条件来描述不等式的性质吗?试用“充分不必要”“必要不充分”“充要”填空:
新知探究
(1)a>b是a+c>b+c的_______条件;
(2)如果c>0,则a>b是ac>bc的_______条件;
(3)如果c<0,则a>b是ac<bc的_______条件.
充要
充要
充要
追问3:不等式还有哪些性质呢?
新知探究
性质4 如果a>b,b>c,那么a>c.(通常称为不等关系的传递性)
证明:因为a-c=(a-b)+(b-c),
又因为a>b,所以a-b>0;
且b>c,所以b-c>0,因此(a-b)+(b-c)>0,
从而a-c>0,即a>c.
性质5 a>b?b<a.
这只要利用a-b=-(b-a)就可以证明.
追问3:不等式还有哪些性质呢?
新知探究
强调:值得注意的是,上述不等式性质对任意满足条件的实数都成立,因此我们可以用任意满足条件的式子去代替其中的字母.
新知探究
问题3 利用前面不等式的性质,我们还可以得到关于不等式的哪些结论?
推论1 如果a+b>c,那么a>c-b.
证明 a+b>c?a+b+(-b)>c+(-b)?a>c-b.
推论1表明,不等式中的任意一项都可以把它的符号变成相反的符号后,从不等式的一边移到另一边.推论1通常称为不等式的移项法则.
新知探究
问题3 利用前面不等式的性质,我们还可以得到关于不等式的哪些结论?
推论2 如果a>b,c>d,那么a+c>b+d.
证明 根据性质1有a>b?a+c>b+c,c>d ?b+c>b+d,
再根据性质4可知a+c>b+d.
新知探究
问题3 利用前面不等式的性质,我们还可以得到关于不等式的哪些结论?
我们把a>b和c>d(或a<b和c<d)这类不等号方向相同的不等式,称为同向不等式.推论2说明,两个同向不等式的两边分别相加,所得到的不等式与原不等式同向.很明显,推论2可以推广为更一般的结论:有限个同向不等式的两边分别相加,所得到的不等式与原不等式同向.
新知探究
例1 (1)比较x2-x和x-2的大小.
(2)已知a,b为正数,且a≠b,比较a3+b3与a2b+ab2的大小.
(1)因为(x2-x)-(x-2)=x2-2x+2=(x-1)2+1,
又因为(x-1)2≥0,所以(x-1)2+1≥1>0,
从而(x2-x)-(x-2)>0,因此x2-x>x-2.
新知探究
例1 (1)比较x2-x和x-2的大小.
(2)已知a,b为正数,且a≠b,比较a3+b3与a2b+ab2的大小.
(2)(a3+b3)-(a2b+ab2)=a3+b3-a2b-ab2
=a2(a-b)-b2(a-b)=(a-b)(a2-b2)
=(a-b)2(a+b).
∵a>0,b>0,且a≠b,
∴(a-b)2>0,a+b>0.
∴(a3+b3)-(a2b+ab2)>0,即a3+b3>a2b+ab2.
新知探究
方法总结:通过比较两式之差的符号来判断两式的大小,这种方法通常称为作差法.作差法的步骤:
(1)作差:对要比较大小的两个代数式作差.
(2)变形:对差进行变形(因式分解或者配方等).
(3)判断差的符号:结合变形的结果及题设条件判断差的符号.
(4)作出结论.
新知探究
其思维过程是作差→变形→判断符号→作出结论.当不能直接得到正或负的结论时,还要考虑通过分类讨论来确定.
新知探究
例2 设a≥b>0,求证:3a3+2b3≥3a2b+2ab2.
解:3a3+2b3-(3a2b+2ab2)=3a2(a-b)+2b2(b-a)
=(3a2-2b2)(a-b).
因为a≥b>0,所以a-b≥0,3a2-2b2>0,
从而(3a2-2b2)(a-b)≥0,
所以3a3+2b3≥3a2b+2ab2.
新知探究
方法总结:(1)简单不等式的证明可直接由已知条件并利用不等式的性质,通过对不等式变形得证.
(2)对于不等号两边都比较复杂的式子,直接利用不等式的性质不易得证,可考虑将不等式的两边作差,然后进行变形,根据条件确定每一个因式(式子)的符号,利用符号法则判断最终的符号,完成证明.这种证明方法常说成是比较法.
新知探究
例3 (1)已知a>b,c<d,求证:a-c>b-d;
(2)已知a>b,ab>0,求证: .
证明:(1)因为a>b,c<d,所以a>b,-c>-d,
根据推论2,得a-c>b-d.
(2)因为ab>0,所以 >0,
又因为a>b,所以a· >b· ,
即 ,因此 .
新知探究
方法总结:从已知条件出发,综合利用各种结果,经过逐步推导最后得到结论的方法,在数学中通常称为综合法.本例与前面的推论所使用的方法都是综合法.综合法中,最重要的推理形式为p?q,其中p是已知或者已经得出的结论,所以综合法的实质就是不断寻找必然成立的结论.在证明不等式时,当然也可直接利用已经证明过的不等式性质等.
归纳小结
回顾本节课,你有什么收获?
(1)什么叫不等式?
(2)如何比较两个实数的大小?
(3)不等式的性质有哪些?
(4)不等式的性质有哪些推论?
(5)本节课学了哪些证明不等式的方法?
作业:教科书P63练习B 1、2、3.
作业布置
再见
