北师大版数学八年级上册6.2 中位数与众数课件(13张)
文档属性
| 名称 | 北师大版数学八年级上册6.2 中位数与众数课件(13张) |  | |
| 格式 | ppt | ||
| 文件大小 | 185.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-04 18:14:22 | ||
图片预览





文档简介
6.1 平均数
第6章 数据的分析
情景导入 生成问题
某公司员工的月工资如下:
员工
经理
副经理
职员A
职员B
职员C
职员D
职员E
职员F
杂工G
月工资(元)
7000
4400
2400
2000
1900
1800
1800
1800
1200
问题:这个公司员工的月平均工资是多少?
这个公司员工收入到底怎样?
你如何看待?
1.经理说平均工资有2700元是否欺骗了应聘者?
2.职员C说他的工资1900元居中等水平什么意思?
3.职员D的工资1800元在上表数据中有什么特点?
没有,月平均工资2700元,指所有员工工资的平均数是2700元,说明公司每月将支付工资总计2700×9=24300(元)
1900元恰好居于所有员工工资的“正中间”---称为中位数
1800元出现次数最多,称为众数
员工
经理
副经理
职员A
职员B
职员C
职员D
职员E
职员F
杂工G
月工资(元)
7000
4400
2400
2000
1900
1800
1800
1800
1200
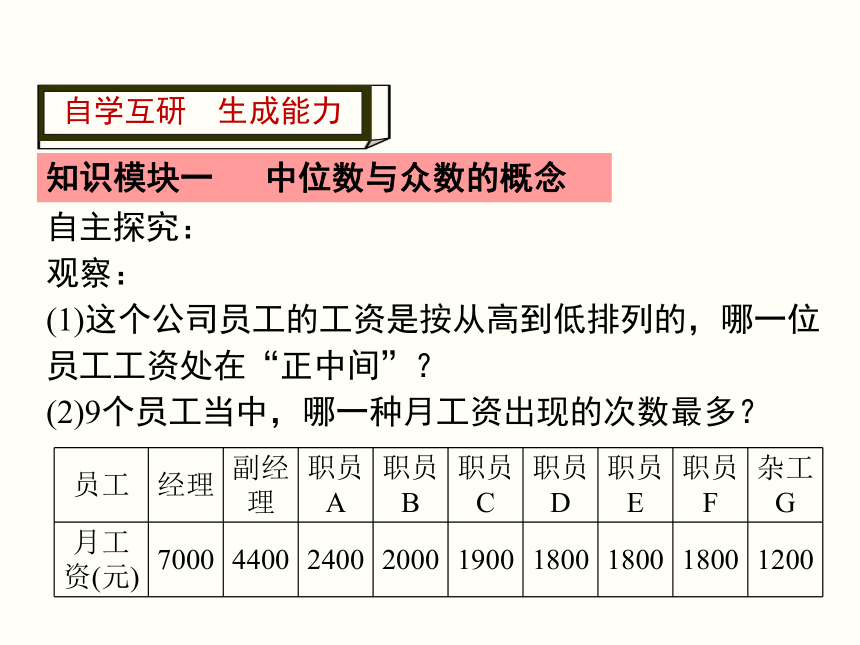
自学互研 生成能力
知识模块一 中位数与众数的概念
自主探究:
观察:
(1)这个公司员工的工资是按从高到低排列的,哪一位员工工资处在“正中间”?
(2)9个员工当中,哪一种月工资出现的次数最多?
员工
经理
副经理
职员A
职员B
职员C
职员D
职员E
职员F
杂工G
月工资(元)
7000
4400
2400
2000
1900
1800
1800
1800
1200
【归纳结论】
一般地,几个数据按大小顺序排列,处于最中间位置的一个数据(或最中间的两个数据的平均数)叫做这组数据的中位数.
一组数据中出现次数最多的那个数据叫做这组数据的众数.
合作探究
讨论:
(1)在上面的问题中,你认为用平均数、中位数和众数中哪个数据描述该公司员工收入的集中趋势更合适?
(2)为什么该公司员工收入的平均数比中位数高得多?
【说明】在同一个问题中分别求平均数、中位数和众数,这是为了比较三个量在描述一组数据集中趋势时的不同角度,从而有助于了解三个概念之间的联系与区别.
知识模块二 平均数、中位数和众数的应用
合作探究
完成下面问题的学习.
做一做:
(1)2011~2012赛季北京金隅队队员身高的平均数、中位数和众数分别是多少?
(2)你课前调查的20位男同学所穿运动鞋尺码的平均数、中位数和众数分别是多少?你认为学校商店应多进哪种尺码的运动鞋?
(3)平均数、中位数和众数都是描述数据集中趋势的统计量,它们各自有哪些特征呢?
它们从不同角度描述了一组数据的“平均水平”.
计算平均数时,所有数据都参加运算,它能充分利用数据所提供的信息,但容易受极端值的影响,应用最为广泛.
中位数的优点是计算简单,只与其在数据中的位置有关.但不能充分利用所有数据的信息.
众数只与其在数据中重复的次数有关,而且往往不是唯一的. 不能充分利用所有的数据信息,而且当各个数据的重复次数大致相等时,众数往往没有特别的意义.
月工资/元 5000 4000 2000 1000 600 500
人数 1 2 5 12 30 6
解:平均数是1000,
众数是600,
中位数是600.
1.某公司56名员工的月工资统计如下:
求该公司员工月工资的平均数、中位数和众数
随堂练习
2.若数据80、81、79、68、75、78、x、82的众数是81,则( )
A.x=79 B.x=80 C.x=81 D.x=82
3.“五一节”黄金周期间,某风景区在7天假期中每天上山旅游的人数统计如下表:其中中位数和众数分别是( )
A.1.2,2 B.2,2.5
C.2,2 D.1.2,2.5
C
C
随堂练习
4.某公司有15名员工,他们所在的部门及相应每人所创的年利润(万元/人.年)如下表所示:
部门
A
B
C
D
E
F
G
人数
1
1
2
4
2
2
3
利润
20
5
2.5
2.1
1.5
1.5
1.2
根据表中提供的信息填空:
1、该公司每人所创年利润的平均数是( )万元,中位数是( )万元,众数是( )万元.
2、你认为应该使用平均数还是中位数来描述该公司每人所创年利润的一般水平?
3.2
2.1
1.5和2.1
中位数
选择合适的数据代表
中位数
众数
课堂小结
第6章 数据的分析
情景导入 生成问题
某公司员工的月工资如下:
员工
经理
副经理
职员A
职员B
职员C
职员D
职员E
职员F
杂工G
月工资(元)
7000
4400
2400
2000
1900
1800
1800
1800
1200
问题:这个公司员工的月平均工资是多少?
这个公司员工收入到底怎样?
你如何看待?
1.经理说平均工资有2700元是否欺骗了应聘者?
2.职员C说他的工资1900元居中等水平什么意思?
3.职员D的工资1800元在上表数据中有什么特点?
没有,月平均工资2700元,指所有员工工资的平均数是2700元,说明公司每月将支付工资总计2700×9=24300(元)
1900元恰好居于所有员工工资的“正中间”---称为中位数
1800元出现次数最多,称为众数
员工
经理
副经理
职员A
职员B
职员C
职员D
职员E
职员F
杂工G
月工资(元)
7000
4400
2400
2000
1900
1800
1800
1800
1200
自学互研 生成能力
知识模块一 中位数与众数的概念
自主探究:
观察:
(1)这个公司员工的工资是按从高到低排列的,哪一位员工工资处在“正中间”?
(2)9个员工当中,哪一种月工资出现的次数最多?
员工
经理
副经理
职员A
职员B
职员C
职员D
职员E
职员F
杂工G
月工资(元)
7000
4400
2400
2000
1900
1800
1800
1800
1200
【归纳结论】
一般地,几个数据按大小顺序排列,处于最中间位置的一个数据(或最中间的两个数据的平均数)叫做这组数据的中位数.
一组数据中出现次数最多的那个数据叫做这组数据的众数.
合作探究
讨论:
(1)在上面的问题中,你认为用平均数、中位数和众数中哪个数据描述该公司员工收入的集中趋势更合适?
(2)为什么该公司员工收入的平均数比中位数高得多?
【说明】在同一个问题中分别求平均数、中位数和众数,这是为了比较三个量在描述一组数据集中趋势时的不同角度,从而有助于了解三个概念之间的联系与区别.
知识模块二 平均数、中位数和众数的应用
合作探究
完成下面问题的学习.
做一做:
(1)2011~2012赛季北京金隅队队员身高的平均数、中位数和众数分别是多少?
(2)你课前调查的20位男同学所穿运动鞋尺码的平均数、中位数和众数分别是多少?你认为学校商店应多进哪种尺码的运动鞋?
(3)平均数、中位数和众数都是描述数据集中趋势的统计量,它们各自有哪些特征呢?
它们从不同角度描述了一组数据的“平均水平”.
计算平均数时,所有数据都参加运算,它能充分利用数据所提供的信息,但容易受极端值的影响,应用最为广泛.
中位数的优点是计算简单,只与其在数据中的位置有关.但不能充分利用所有数据的信息.
众数只与其在数据中重复的次数有关,而且往往不是唯一的. 不能充分利用所有的数据信息,而且当各个数据的重复次数大致相等时,众数往往没有特别的意义.
月工资/元 5000 4000 2000 1000 600 500
人数 1 2 5 12 30 6
解:平均数是1000,
众数是600,
中位数是600.
1.某公司56名员工的月工资统计如下:
求该公司员工月工资的平均数、中位数和众数
随堂练习
2.若数据80、81、79、68、75、78、x、82的众数是81,则( )
A.x=79 B.x=80 C.x=81 D.x=82
3.“五一节”黄金周期间,某风景区在7天假期中每天上山旅游的人数统计如下表:其中中位数和众数分别是( )
A.1.2,2 B.2,2.5
C.2,2 D.1.2,2.5
C
C
随堂练习
4.某公司有15名员工,他们所在的部门及相应每人所创的年利润(万元/人.年)如下表所示:
部门
A
B
C
D
E
F
G
人数
1
1
2
4
2
2
3
利润
20
5
2.5
2.1
1.5
1.5
1.2
根据表中提供的信息填空:
1、该公司每人所创年利润的平均数是( )万元,中位数是( )万元,众数是( )万元.
2、你认为应该使用平均数还是中位数来描述该公司每人所创年利润的一般水平?
3.2
2.1
1.5和2.1
中位数
选择合适的数据代表
中位数
众数
课堂小结
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
