人教版九年级上数学24.4扇形的面积公式课件(17张)
文档属性
| 名称 | 人教版九年级上数学24.4扇形的面积公式课件(17张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-04 00:00:00 | ||
图片预览




文档简介
24.4 弧长和扇形面积(第2课时)
九年级 上册
一、创设情境,揭示课题
情景一 多脚的周华家共有八口人,十月年期间,在蒙自一家蛋糕店工作的姐姐回到家中过年,给家人带回了一个14寸的圆形蛋糕。晚饭过后,全家人一起到客厅分享姐姐带回的蛋糕,他们这样分的:
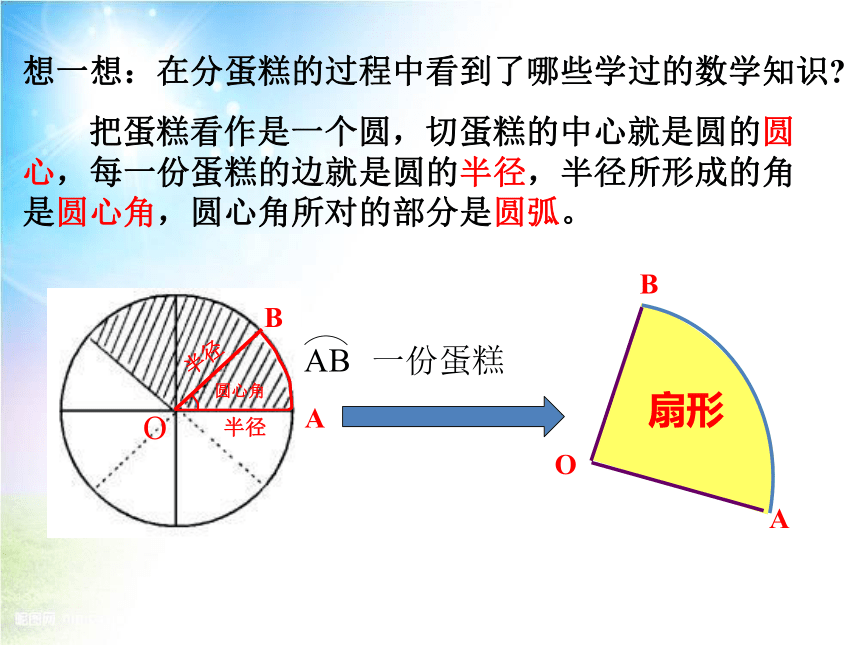
想一想:在分蛋糕的过程中看到了哪些学过的数学知识?
B
A
圆心角
把蛋糕看作是一个圆,切蛋糕的中心就是圆的圆心,每一份蛋糕的边就是圆的半径,半径所形成的角是圆心角,圆心角所对的部分是圆弧。
O
半径
半径
AB
O
B
A
一份蛋糕
扇形
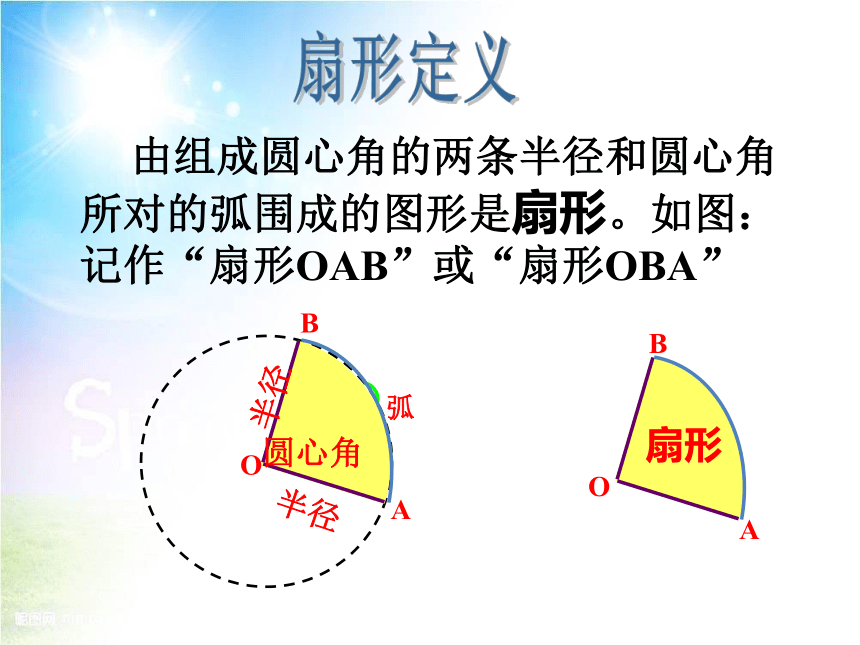
由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。如图:记作“扇形OAB”或“扇形OBA”
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
情景二 分完蛋糕后,全家人开心的围桌而坐,聊天交谈。下面是姐姐和周华的对话。
姐姐:弟弟,姐姐考考你。今晚我们分蛋糕,每个人获得蛋糕面积是多少呢?
周华思考一会,说到:姐,这难不倒我。但你必须先回答我一个问题?
姐姐:你说吧,什么问题?
周华:至少给我这个蛋糕的一个信息吧!
姐姐想了想,说:这个蛋糕是14寸的,也就是说这个蛋糕直径大约是46cm。
周华沉默一分钟后,答道:我们每个人分得蛋糕的面积是… …
思考:请聪明的你也想一想周华回答了什么呢?
1
8
πR2
R
.
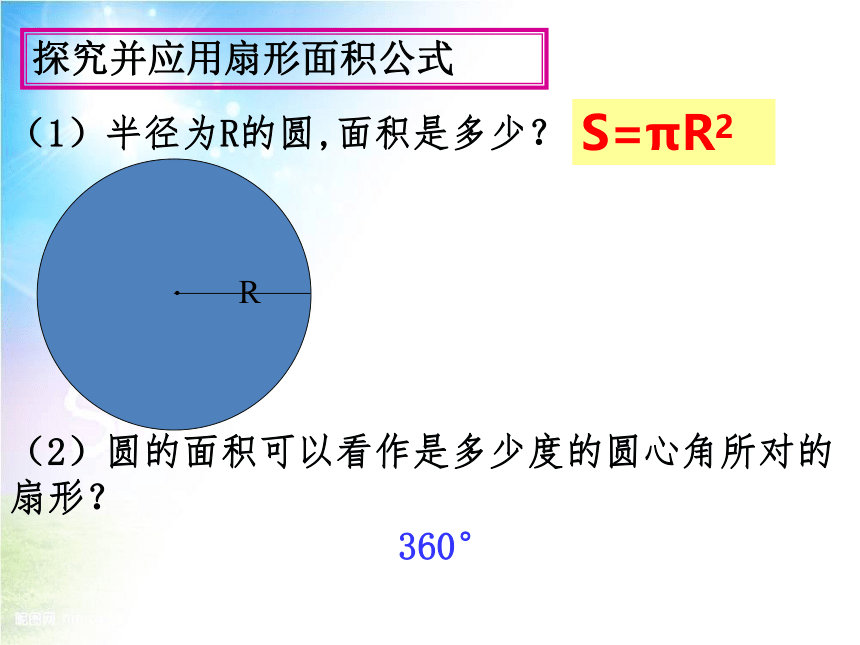
(1)半径为R的圆,面积是多少?
360°
(2)圆的面积可以看作是多少度的圆心角所对的扇形?
S=πR2
探究并应用扇形面积公式
我们知道:圆的面积是 .那么
圆心角是1°的扇形面积是圆面积的
,即
动动脑:
(3)n°圆心角所对的扇形面积是1°圆心角所对的扇形面积的多少倍?
(4)n°圆心角所对扇形面积是多少?
(1)90°圆心角所对的扇形面积是1°圆心角所对的扇形面积的多少倍?
90 倍
(2)90°圆心角所对扇形面积是多少?
我们刚刚学过圆心角是1°的扇形面积是:
90×
若设⊙O半径为R,n°的圆心角所对的扇形面积为S,则:
n°
1、已知扇形的圆心角为120°,半径
为2,则这个扇形的面积,S扇=
2、已知扇形面积为 ,圆心角为120°,则这个扇形的半径R=____.
2
3、扇形面积大小( )
(A)只与半径长短有关
(B)只与圆心角大小有关
(C)与圆心角的大小、半径的长短有关
C
例:如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积。(精确到0.01cm)。
C
O
B
A
D
分析:要求图中阴影(弓形)面积,没有直接的公式,需要转化为图形组合的和差问题,即扇形面积与三角形面积的差。容易想到做辅助线利用垂径定理,先根据公式分别求出扇形和三角形面积,问题得到解决。
∴S= S扇形OAB- SΔOAB≈0.22(m2)
SΔOAB=
1
2
×AB×OD=
可得AD=0.3
AD2+ OD2=OA2
在RtΔAOD中
∴ S扇形OAB=
∴ ∠AOB=120°
同理可证∠BOD=60°
∴∠OAD=30°,∠AOD=60°
1
2
∴OD=OC-CD=0.3= OC
解:连接OA,OB,过O作OC⊥AB于点D .
∵OC=0.6,CD=0.3
又∵ OC⊥AB,
∴AB=0.6
答:截面上有水部分的面积约为0.22m2。
O
D
A
B
C
A
B
O
O
比较扇形面积与弧长公式, 用弧长表示扇形面积:
这节课你有哪些收获?
作业布置:
课本116页第8题
九年级 上册
一、创设情境,揭示课题
情景一 多脚的周华家共有八口人,十月年期间,在蒙自一家蛋糕店工作的姐姐回到家中过年,给家人带回了一个14寸的圆形蛋糕。晚饭过后,全家人一起到客厅分享姐姐带回的蛋糕,他们这样分的:
想一想:在分蛋糕的过程中看到了哪些学过的数学知识?
B
A
圆心角
把蛋糕看作是一个圆,切蛋糕的中心就是圆的圆心,每一份蛋糕的边就是圆的半径,半径所形成的角是圆心角,圆心角所对的部分是圆弧。
O
半径
半径
AB
O
B
A
一份蛋糕
扇形
由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。如图:记作“扇形OAB”或“扇形OBA”
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
情景二 分完蛋糕后,全家人开心的围桌而坐,聊天交谈。下面是姐姐和周华的对话。
姐姐:弟弟,姐姐考考你。今晚我们分蛋糕,每个人获得蛋糕面积是多少呢?
周华思考一会,说到:姐,这难不倒我。但你必须先回答我一个问题?
姐姐:你说吧,什么问题?
周华:至少给我这个蛋糕的一个信息吧!
姐姐想了想,说:这个蛋糕是14寸的,也就是说这个蛋糕直径大约是46cm。
周华沉默一分钟后,答道:我们每个人分得蛋糕的面积是… …
思考:请聪明的你也想一想周华回答了什么呢?
1
8
πR2
R
.
(1)半径为R的圆,面积是多少?
360°
(2)圆的面积可以看作是多少度的圆心角所对的扇形?
S=πR2
探究并应用扇形面积公式
我们知道:圆的面积是 .那么
圆心角是1°的扇形面积是圆面积的
,即
动动脑:
(3)n°圆心角所对的扇形面积是1°圆心角所对的扇形面积的多少倍?
(4)n°圆心角所对扇形面积是多少?
(1)90°圆心角所对的扇形面积是1°圆心角所对的扇形面积的多少倍?
90 倍
(2)90°圆心角所对扇形面积是多少?
我们刚刚学过圆心角是1°的扇形面积是:
90×
若设⊙O半径为R,n°的圆心角所对的扇形面积为S,则:
n°
1、已知扇形的圆心角为120°,半径
为2,则这个扇形的面积,S扇=
2、已知扇形面积为 ,圆心角为120°,则这个扇形的半径R=____.
2
3、扇形面积大小( )
(A)只与半径长短有关
(B)只与圆心角大小有关
(C)与圆心角的大小、半径的长短有关
C
例:如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积。(精确到0.01cm)。
C
O
B
A
D
分析:要求图中阴影(弓形)面积,没有直接的公式,需要转化为图形组合的和差问题,即扇形面积与三角形面积的差。容易想到做辅助线利用垂径定理,先根据公式分别求出扇形和三角形面积,问题得到解决。
∴S= S扇形OAB- SΔOAB≈0.22(m2)
SΔOAB=
1
2
×AB×OD=
可得AD=0.3
AD2+ OD2=OA2
在RtΔAOD中
∴ S扇形OAB=
∴ ∠AOB=120°
同理可证∠BOD=60°
∴∠OAD=30°,∠AOD=60°
1
2
∴OD=OC-CD=0.3= OC
解:连接OA,OB,过O作OC⊥AB于点D .
∵OC=0.6,CD=0.3
又∵ OC⊥AB,
∴AB=0.6
答:截面上有水部分的面积约为0.22m2。
O
D
A
B
C
A
B
O
O
比较扇形面积与弧长公式, 用弧长表示扇形面积:
这节课你有哪些收获?
作业布置:
课本116页第8题
同课章节目录
