《2.2.4均值不等式及其应用》第1课时课件(26张PPT)
文档属性
| 名称 | 《2.2.4均值不等式及其应用》第1课时课件(26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 252.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-03 00:00:00 | ||
图片预览








文档简介
2.2.4 均值不等式及其应用
第1课时
问题1 阅读课本第71~75页,回答下列问题:
整体概览
(1)本节将要研究哪类问题?
(2)本节研究的起点是什么?目标是什么?
问题1 阅读课本第71~75页,回答下列问题:
整体概览
(1)本节将要研究均值不等式及其应用.(2)起点是不等式的性质以及比较法,目标是知道均值不等式,会证明均值不等式定理,会用均值不等式解决简单的最大(小)问题.进一步提升数学运算、逻辑推理等素养.
(1)本节将要研究哪类问题?
(2)本节研究的起点是什么?目标是什么?
情境与问题
问题 给定两个正数a,b,数 称为a,b的算术平均值;数 称为a,b的几何平均值.两个数的算术平均值,实质上是这两个数在数轴上对应的点的中点坐标,那么几何平均值有什么几何意义呢?两个数的算术平均值和几何平均值之间有什么相对大小关系呢?
情境与问题
【尝试与发现】
(1)假设一个矩形的长和宽分别为a和b,求与这个矩形周长相等的正方形的边长,以及与这个矩形面积相等的正方形的边长,并比较这两个边长的大小;
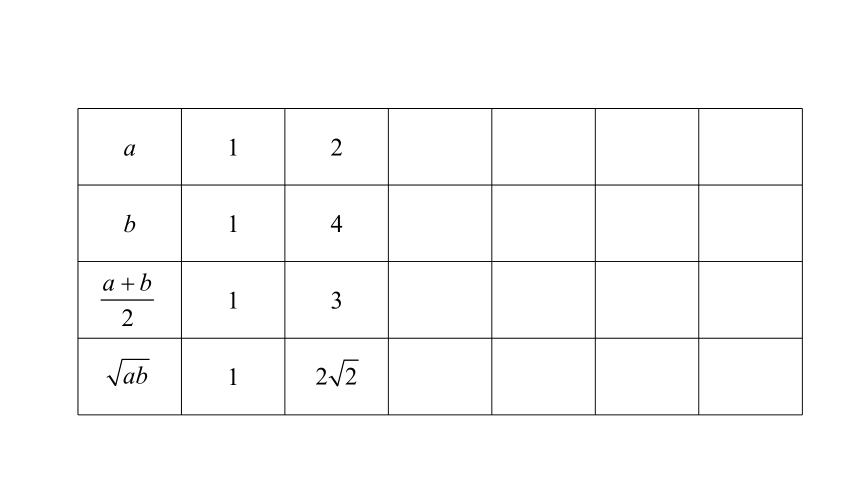
(2)如下表所示,再任意取几组正数,算出它们的算术平均值和几何平均值,猜测一般情况下两个数的算术平均值与几何平均值的相对大小,并根据(1)说出结论的几何意义.
情境与问题
{616DA210-FB5B-4158-B5E0-FEB733F419BA}a
1
2
b
1
4
1
3
1
新知探究
均值不等式 如果a,b都是正数,那么 ,
当且仅当a=b时,等号成立.
证明 因为a,b都是正数,所以
即
而且,等号成立时,当且仅当 ,即a=b.
新知探究
均值不等式 如果a,b都是正数,那么 ,
当且仅当a=b时,等号成立.
值得注意的是,均值不等式中的a,b可以是任意正实数,因此我们可以代入任意满足条件的数或式子,比如 一定是正确的.
新知探究
均值不等式 如果a,b都是正数,那么 ,
当且仅当a=b时,等号成立.
综合法证明如下:
因为(a-b)2≥0,所以a2+b2-2ab≥0,
所以a2+b2+2ab-4ab≥0,
即(a+b)2≥4ab.
又因为a>0,b>0,所以a+b≥ ,
显然,当且仅当(a-b)2=0,即a=b时,等号成立.
即 .
新知探究
问题2 均值不等式也称为基本不等式(基本不等式中的a,b还可以为零),其实质是:两个正实数的算术平均值不小于它们的几何平均值.那么,均值不等式有什么几何意义呢?
将均值不等式两边平方可得 ≥ab.
如果矩形的长和宽分别为a和b,那么矩形的面积为ab, 可以看成与矩形周长相等的正方形的面积,因此均值不等式的一个几何意义为:所有周长一定的矩形中,正方形的面积最大.
新知探究
【想一想】你能推广这个结论吗?比如所有周长相等的三角形中,什么样的三角形面积最大?平面上,周长相等的所有封闭图形中,什么样的图形面积最大?
正三角形,圆
新知探究
问题3 如图所示半圆中,AB为直径,O为圆心.已知AC=a,BC=b,D为半圆上一点,且DC⊥AB,算出OD和CD,是否可以给出均值不等式的另一个几何意义?
A
B
D
O
C
在RtΔABD中,由于DC⊥AB,利用射影定理可得CD= ,又CO=
,由图可知CO≥CD,所以 ,变形为a+b≥ .
结论:均值不等式的几何意义是:一个圆的直径大于等于垂直该直径的弦.
新知探究
例1 (1)已知x>0,求y=x+ 的最小值,并说明x为何值时y取得最小值.
(2)已知x∈(-1,3),求y=(1+x)(3-x)的最大值,以及y取得最大值时x的值.
(3)求函数y=x(1-x),x∈[ ,1)的最大值.
新知探究
例1 (1)已知x>0,求y=x+ 的最小值,并说明x为何值时y取得最小值.
解:(1)因为x>0,所以根据均值不等式有
解得x=1或x=-1(舍).
其中等号成立当且仅当x= ,即x2=1,
因此x=1时,y取得最小值2.
新知探究
例1 (2)已知x∈(-1,3),求y=(1+x)(3-x)的最大值,以及y取得最大值时x的值.
解:(2)当x∈(-1,3)时,一1<x<3,因此1+x>0,3一x>0.
当且仅当1+x=3-x,即x=1时,等号成立.
从而(1+x)(3-x)≤4,即y≤4.
由均值不等式可得 ,
从而x=1时,y取得最大值4.
解: (3)错解:由 ≤x<1,易知1-x>0,
新知探究
例1 (3)求函数y=x(1-x),x∈[ ,1)的最大值.
从而y=x(1-x)≤ = .所以y的最大值为 .
正解:y=x(1-x)=-x2+x=-(x- )2+ ,
当x= 时,ymax= .
新知探究
(1)在利用均值不等式求最值时要注意“一正、二定、三相等”:一正,a,b均为正数;二定,不等式一边为定值;三相等,不等式中的等号能取到,即a=b有解.(2)两个正数的积为常数时,它们的和有最小值;两个正数的和为常数时,它们的积有最大值.(3)利用均值不等式求最值时,等号必须取得到才能求出最值,若题设条件中的限制条件使等号不能成立,则要转换到另一种形式解答.
新知探究
例2 (1)已知矩形的面积为100,则这个矩形的长、宽各为多少时,矩形的周长最短?最短周长是多少?
(2)已知矩形的周长为36,则这个矩形的长、宽各为多少时,它的面积最大?最大面积是多少?
在(1)中,矩形的长与宽的积是一个常数,要求长与宽之和的两倍的最小值;在(2)中,矩形的长与宽之和的两倍是一个常数,要求长与宽的积的最大值.
新知探究
例2 (1)已知矩形的面积为100,则这个矩形的长、宽各为多少时,矩形的周长最短?最短周长是多少?
解:(1)设矩形的长与宽分别为x与y,依题意得xy=100.
因此,当矩形的长和宽都是10时,它的周长最短,最短周长为40.
当且仅当x=y时,等号成立,
所以2(x+y)≥40.
因为x>0,y>0,所以
由 ,可知此时x=y=10.
新知探究
例2 (2)已知矩形的周长为36,则这个矩形的长、宽各为多少时,它的面积最大?最大面积是多少?
解:(2)设矩形的长与宽分别为x与y,
依题意得2(x+y)=36,即x+y=18.
因为x>0,y>0,所以
因此 ≤9,即xy≤81.
当且仅当x=y时,等号成立,由 ,可知此时x=y=9.
因此,当矩形的长和宽都是9时,它的面积最大,最大面积为81.
新知探究
方法总结:求实际问题中最值的一般思路:(1)读懂题意,设出变量,列出函数关系式;
(3)在定义域内,求函数的最大值或最小值时,一般先考虑用均值不等式,当用均值不等式求最值的条件不具备时,再考虑利用第三章要学习的函数的单调性求解.
(2)把实际问题转化为求函数的最大值或最小值问题;
(4)正确地写出答案.
新知探究
(1)已知a为大于0的常数,x>0,求y=x+ 的最小值,并求y取得最小值时相应的x的值;
(2)已知x<0,求y=x+ 的最大值,并求y取得最大值时相应x的值;
(3)已知x>1,求y=x+ 的最小值,并求y取得最小值时相应x的值;
(4)已知x<1,求y=x+ 的最大值,并求y取得最大值时相应x的值.
新知探究
(2)当x=-1时,y有最大值为一2;
(3)当x=2时,y有最小值为3;
(4)当x=0时,y有最大值为一1.
参考答案:(1)当x= 时,y有最小值为 ;
归纳小结
回顾本节课,你有什么收获?
(1)什么叫均值不等式?如何证明?
(2)均值不等式的几何意义是什么?
(3)如何利用均值不等式求最值?
作业:教科书P76练习B 1,2,4.
作业布置
再见
第1课时
问题1 阅读课本第71~75页,回答下列问题:
整体概览
(1)本节将要研究哪类问题?
(2)本节研究的起点是什么?目标是什么?
问题1 阅读课本第71~75页,回答下列问题:
整体概览
(1)本节将要研究均值不等式及其应用.(2)起点是不等式的性质以及比较法,目标是知道均值不等式,会证明均值不等式定理,会用均值不等式解决简单的最大(小)问题.进一步提升数学运算、逻辑推理等素养.
(1)本节将要研究哪类问题?
(2)本节研究的起点是什么?目标是什么?
情境与问题
问题 给定两个正数a,b,数 称为a,b的算术平均值;数 称为a,b的几何平均值.两个数的算术平均值,实质上是这两个数在数轴上对应的点的中点坐标,那么几何平均值有什么几何意义呢?两个数的算术平均值和几何平均值之间有什么相对大小关系呢?
情境与问题
【尝试与发现】
(1)假设一个矩形的长和宽分别为a和b,求与这个矩形周长相等的正方形的边长,以及与这个矩形面积相等的正方形的边长,并比较这两个边长的大小;
(2)如下表所示,再任意取几组正数,算出它们的算术平均值和几何平均值,猜测一般情况下两个数的算术平均值与几何平均值的相对大小,并根据(1)说出结论的几何意义.
情境与问题
{616DA210-FB5B-4158-B5E0-FEB733F419BA}a
1
2
b
1
4
1
3
1
新知探究
均值不等式 如果a,b都是正数,那么 ,
当且仅当a=b时,等号成立.
证明 因为a,b都是正数,所以
即
而且,等号成立时,当且仅当 ,即a=b.
新知探究
均值不等式 如果a,b都是正数,那么 ,
当且仅当a=b时,等号成立.
值得注意的是,均值不等式中的a,b可以是任意正实数,因此我们可以代入任意满足条件的数或式子,比如 一定是正确的.
新知探究
均值不等式 如果a,b都是正数,那么 ,
当且仅当a=b时,等号成立.
综合法证明如下:
因为(a-b)2≥0,所以a2+b2-2ab≥0,
所以a2+b2+2ab-4ab≥0,
即(a+b)2≥4ab.
又因为a>0,b>0,所以a+b≥ ,
显然,当且仅当(a-b)2=0,即a=b时,等号成立.
即 .
新知探究
问题2 均值不等式也称为基本不等式(基本不等式中的a,b还可以为零),其实质是:两个正实数的算术平均值不小于它们的几何平均值.那么,均值不等式有什么几何意义呢?
将均值不等式两边平方可得 ≥ab.
如果矩形的长和宽分别为a和b,那么矩形的面积为ab, 可以看成与矩形周长相等的正方形的面积,因此均值不等式的一个几何意义为:所有周长一定的矩形中,正方形的面积最大.
新知探究
【想一想】你能推广这个结论吗?比如所有周长相等的三角形中,什么样的三角形面积最大?平面上,周长相等的所有封闭图形中,什么样的图形面积最大?
正三角形,圆
新知探究
问题3 如图所示半圆中,AB为直径,O为圆心.已知AC=a,BC=b,D为半圆上一点,且DC⊥AB,算出OD和CD,是否可以给出均值不等式的另一个几何意义?
A
B
D
O
C
在RtΔABD中,由于DC⊥AB,利用射影定理可得CD= ,又CO=
,由图可知CO≥CD,所以 ,变形为a+b≥ .
结论:均值不等式的几何意义是:一个圆的直径大于等于垂直该直径的弦.
新知探究
例1 (1)已知x>0,求y=x+ 的最小值,并说明x为何值时y取得最小值.
(2)已知x∈(-1,3),求y=(1+x)(3-x)的最大值,以及y取得最大值时x的值.
(3)求函数y=x(1-x),x∈[ ,1)的最大值.
新知探究
例1 (1)已知x>0,求y=x+ 的最小值,并说明x为何值时y取得最小值.
解:(1)因为x>0,所以根据均值不等式有
解得x=1或x=-1(舍).
其中等号成立当且仅当x= ,即x2=1,
因此x=1时,y取得最小值2.
新知探究
例1 (2)已知x∈(-1,3),求y=(1+x)(3-x)的最大值,以及y取得最大值时x的值.
解:(2)当x∈(-1,3)时,一1<x<3,因此1+x>0,3一x>0.
当且仅当1+x=3-x,即x=1时,等号成立.
从而(1+x)(3-x)≤4,即y≤4.
由均值不等式可得 ,
从而x=1时,y取得最大值4.
解: (3)错解:由 ≤x<1,易知1-x>0,
新知探究
例1 (3)求函数y=x(1-x),x∈[ ,1)的最大值.
从而y=x(1-x)≤ = .所以y的最大值为 .
正解:y=x(1-x)=-x2+x=-(x- )2+ ,
当x= 时,ymax= .
新知探究
(1)在利用均值不等式求最值时要注意“一正、二定、三相等”:一正,a,b均为正数;二定,不等式一边为定值;三相等,不等式中的等号能取到,即a=b有解.(2)两个正数的积为常数时,它们的和有最小值;两个正数的和为常数时,它们的积有最大值.(3)利用均值不等式求最值时,等号必须取得到才能求出最值,若题设条件中的限制条件使等号不能成立,则要转换到另一种形式解答.
新知探究
例2 (1)已知矩形的面积为100,则这个矩形的长、宽各为多少时,矩形的周长最短?最短周长是多少?
(2)已知矩形的周长为36,则这个矩形的长、宽各为多少时,它的面积最大?最大面积是多少?
在(1)中,矩形的长与宽的积是一个常数,要求长与宽之和的两倍的最小值;在(2)中,矩形的长与宽之和的两倍是一个常数,要求长与宽的积的最大值.
新知探究
例2 (1)已知矩形的面积为100,则这个矩形的长、宽各为多少时,矩形的周长最短?最短周长是多少?
解:(1)设矩形的长与宽分别为x与y,依题意得xy=100.
因此,当矩形的长和宽都是10时,它的周长最短,最短周长为40.
当且仅当x=y时,等号成立,
所以2(x+y)≥40.
因为x>0,y>0,所以
由 ,可知此时x=y=10.
新知探究
例2 (2)已知矩形的周长为36,则这个矩形的长、宽各为多少时,它的面积最大?最大面积是多少?
解:(2)设矩形的长与宽分别为x与y,
依题意得2(x+y)=36,即x+y=18.
因为x>0,y>0,所以
因此 ≤9,即xy≤81.
当且仅当x=y时,等号成立,由 ,可知此时x=y=9.
因此,当矩形的长和宽都是9时,它的面积最大,最大面积为81.
新知探究
方法总结:求实际问题中最值的一般思路:(1)读懂题意,设出变量,列出函数关系式;
(3)在定义域内,求函数的最大值或最小值时,一般先考虑用均值不等式,当用均值不等式求最值的条件不具备时,再考虑利用第三章要学习的函数的单调性求解.
(2)把实际问题转化为求函数的最大值或最小值问题;
(4)正确地写出答案.
新知探究
(1)已知a为大于0的常数,x>0,求y=x+ 的最小值,并求y取得最小值时相应的x的值;
(2)已知x<0,求y=x+ 的最大值,并求y取得最大值时相应x的值;
(3)已知x>1,求y=x+ 的最小值,并求y取得最小值时相应x的值;
(4)已知x<1,求y=x+ 的最大值,并求y取得最大值时相应x的值.
新知探究
(2)当x=-1时,y有最大值为一2;
(3)当x=2时,y有最小值为3;
(4)当x=0时,y有最大值为一1.
参考答案:(1)当x= 时,y有最小值为 ;
归纳小结
回顾本节课,你有什么收获?
(1)什么叫均值不等式?如何证明?
(2)均值不等式的几何意义是什么?
(3)如何利用均值不等式求最值?
作业:教科书P76练习B 1,2,4.
作业布置
再见
