《2.2.4均值不等式及其应用》第2课时课件(19张PPT)
文档属性
| 名称 | 《2.2.4均值不等式及其应用》第2课时课件(19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 307.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-03 00:00:00 | ||
图片预览






文档简介
2.2.4 均值不等式及其应用
第2课时
问题1 阅读课本第71~75页,回答下列问题:
整体概览
(1)本节将要研究均值不等式及其应用.(2)起点是不等式的性质以及比较法,目标是知道均值不等式,会证明均值不等式定理,会用均值不等式解决简单的最大(小)问题.进一步提升数学运算、逻辑推理等素养.
(1)本节将要研究哪类问题?
(2)本节研究的起点是什么?目标是什么?
情境与问题
复习:上节课我们一起学习了均值不等式,请同学们回顾一下均值不等式的内容,以及我们利用均值不等式可以解决什么样的问题?
如果a,b都是正数,那么 ,当且仅当a=b时,等号成立.利用均值不等式可以求最值、解决实际应用问题等.
问题:我们利用均值不等式还能解决什么问题呢?
新知探究
问题2 我们利用均值不等式可以证明不等式,可以直接利用 (a,b都是正数),也可使用a+b≥ .
你还有哪些变形呢?
新知探究
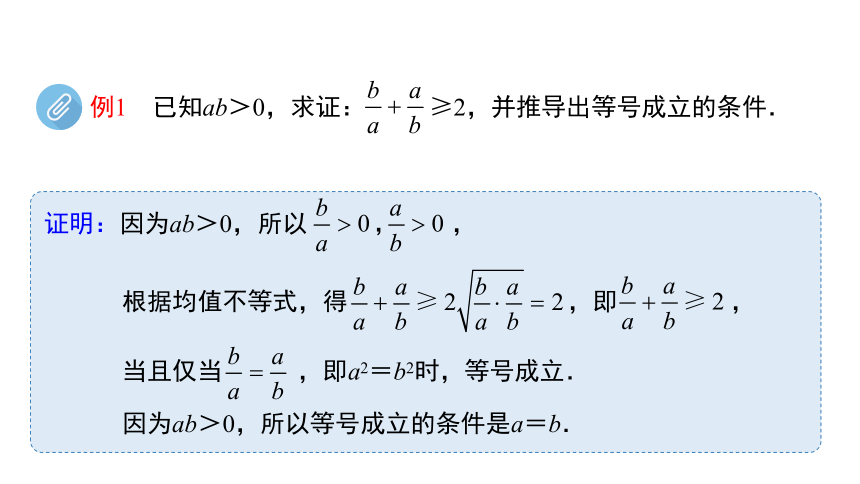
例1 已知ab>0,求证: ≥2,并推导出等号成立的条件.
证明:因为ab>0,所以 ,
根据均值不等式,得 ,即 ,
因为ab>0,所以等号成立的条件是a=b.
当且仅当 ,即a2=b2时,等号成立.
新知探究
例2 已知a,b是实数,求证:a2+b2≥2ab.
证明:因为a2+b2-2ab=(a-b)2≥0,
并说明等号成立的条件.
所以a2+b2-2ab≥0,即a2+b2≥2ab.
等号成立时,当且仅当(a-b)2=0,即a=b.
新知探究
例2的结论也是经常要用的.不难看出,均值不等式与例5的结论既有联系,又有区别.
区别在于例2中去掉了a,b是正数的条件,联系在于均值不等式可以看成例2结论的一种特殊情况.
假设图中直角三角形的直角边分别为a,b,则显然图中大正方形的面积大于四个直角三角形的面积之和,即a2+b2≥2ab,
当且仅当小正方形的面积为0即a=b时取等号.
新知探究
例3 已知a,b∈R,求证:
证明:(1)因为a2+b2≥2ab,两边同时加上2ab,得
a2+b2+2ab≥4ab,
即(a+b)2≥4ab;
(1)(a+b)2≥4ab;
(2)2(a2+b2)≥(a+b)2.
新知探究
例3 已知a,b∈R,求证:
证明:(2)因为a2+b2≥2ab,两边同时加上a2+b2,得
2(a2+b2)≥a2+b2+2ab,
即2(a2+b2)≥(a+b)2.
(1)(a+b)2≥4ab;
(2)2(a2+b2)≥(a+b)2.
新知探究
(a+b)2≥4ab以及2(a2+b2)≥(a+b)2都是均值不等式的变形,又其中2(a2+b2)≥(a+b)2又常变形为 .
新知探究
例4 (1)已知a,b,c?R,求证:a2+b2+c2≥ab+bc+ca;
证明: (1)由a2+b2≥2ab,b2+c2≥2bc,c2+a2≥2ca,
三个不等式相加即能得证;
(3)已知a2+b2=1,x2+y2=1,求证:ax+by≤1.
(2)已知a,b,c为正实数,求证: ≥abc;
新知探究
例4 (1)已知a,b,c?R,求证:a2+b2+c2≥ab+bc+ca;
证明: (2)注意到a2b2+b2c2≥2ab2c,b2c2+c2a2≥2bc2a,
c2a2+a2b2≥2ca2b即可;
(3)已知a2+b2=1,x2+y2=1,求证:ax+by≤1.
(2)已知a,b,c为正实数,求证: ≥abc;
新知探究
例4 (1)已知a,b,c?R,求证:a2+b2+c2≥ab+bc+ca;
证明: (3)注意到a2十x2≥2ax,b2+y2≥2by,两式相加即可得到.
(3)已知a2+b2=1,x2+y2=1,求证:ax+by≤1.
(2)已知a,b,c为正实数,求证: ≥abc;
新知探究
方法总结:利用均值不等式证明不等式的两种题型:(1)无附加条件的不等式的证明.其解题思路:观察待证不等式的结构形式,若不能直接使用均值不等式,则结合左、右两边的结构特征,进行拆项、变形、配凑等,使之达到使用均值不等式的条件.(2)有附加条件的不等式的证明.观察已知条件与待证不等式之间的关系,恰当地使用已知条件,条件的巧妙代换是一种较为重要的变形.
新知探究
【探索与研究】用Excel或其他计算机软件,完成下列数学实验:
(1)任取多组三个正教a,b,c,计算 和 运后,比较它们的大小,总结出一般规律;
(2)对四个正数、五个正数做同样的实验,总结出普遍规律.
一般地, ,当且仅当a1=a2=…=an时,等号成立.
归纳小结
回顾本节课,你有什么收获?
(1)均值不等式有哪些变形?如何证明?
(2)如何利用均值不等式及其变形证明不等式?
利用均值不等式证明不等式的注意点:
(1)多次使用均值不等式时,要注意等号能否成立.
(2)累加法是不等式证明中的一种常用方法,证明不等式时注意使用.
(3)对不能直接使用均值不等式的证明可重新组合,达到使用均值不等式的条件.
作业:教科书P76练习B 3.
作业布置
作业布置
已知a>0,b>0,a+b=1,求证:(1+ )(1+ )≥9.
补
因为a>0,b>0,a+b=1,
所以
同理
故
所以 ,当且仅当a=b= 时取等号.
再见
第2课时
问题1 阅读课本第71~75页,回答下列问题:
整体概览
(1)本节将要研究均值不等式及其应用.(2)起点是不等式的性质以及比较法,目标是知道均值不等式,会证明均值不等式定理,会用均值不等式解决简单的最大(小)问题.进一步提升数学运算、逻辑推理等素养.
(1)本节将要研究哪类问题?
(2)本节研究的起点是什么?目标是什么?
情境与问题
复习:上节课我们一起学习了均值不等式,请同学们回顾一下均值不等式的内容,以及我们利用均值不等式可以解决什么样的问题?
如果a,b都是正数,那么 ,当且仅当a=b时,等号成立.利用均值不等式可以求最值、解决实际应用问题等.
问题:我们利用均值不等式还能解决什么问题呢?
新知探究
问题2 我们利用均值不等式可以证明不等式,可以直接利用 (a,b都是正数),也可使用a+b≥ .
你还有哪些变形呢?
新知探究
例1 已知ab>0,求证: ≥2,并推导出等号成立的条件.
证明:因为ab>0,所以 ,
根据均值不等式,得 ,即 ,
因为ab>0,所以等号成立的条件是a=b.
当且仅当 ,即a2=b2时,等号成立.
新知探究
例2 已知a,b是实数,求证:a2+b2≥2ab.
证明:因为a2+b2-2ab=(a-b)2≥0,
并说明等号成立的条件.
所以a2+b2-2ab≥0,即a2+b2≥2ab.
等号成立时,当且仅当(a-b)2=0,即a=b.
新知探究
例2的结论也是经常要用的.不难看出,均值不等式与例5的结论既有联系,又有区别.
区别在于例2中去掉了a,b是正数的条件,联系在于均值不等式可以看成例2结论的一种特殊情况.
假设图中直角三角形的直角边分别为a,b,则显然图中大正方形的面积大于四个直角三角形的面积之和,即a2+b2≥2ab,
当且仅当小正方形的面积为0即a=b时取等号.
新知探究
例3 已知a,b∈R,求证:
证明:(1)因为a2+b2≥2ab,两边同时加上2ab,得
a2+b2+2ab≥4ab,
即(a+b)2≥4ab;
(1)(a+b)2≥4ab;
(2)2(a2+b2)≥(a+b)2.
新知探究
例3 已知a,b∈R,求证:
证明:(2)因为a2+b2≥2ab,两边同时加上a2+b2,得
2(a2+b2)≥a2+b2+2ab,
即2(a2+b2)≥(a+b)2.
(1)(a+b)2≥4ab;
(2)2(a2+b2)≥(a+b)2.
新知探究
(a+b)2≥4ab以及2(a2+b2)≥(a+b)2都是均值不等式的变形,又其中2(a2+b2)≥(a+b)2又常变形为 .
新知探究
例4 (1)已知a,b,c?R,求证:a2+b2+c2≥ab+bc+ca;
证明: (1)由a2+b2≥2ab,b2+c2≥2bc,c2+a2≥2ca,
三个不等式相加即能得证;
(3)已知a2+b2=1,x2+y2=1,求证:ax+by≤1.
(2)已知a,b,c为正实数,求证: ≥abc;
新知探究
例4 (1)已知a,b,c?R,求证:a2+b2+c2≥ab+bc+ca;
证明: (2)注意到a2b2+b2c2≥2ab2c,b2c2+c2a2≥2bc2a,
c2a2+a2b2≥2ca2b即可;
(3)已知a2+b2=1,x2+y2=1,求证:ax+by≤1.
(2)已知a,b,c为正实数,求证: ≥abc;
新知探究
例4 (1)已知a,b,c?R,求证:a2+b2+c2≥ab+bc+ca;
证明: (3)注意到a2十x2≥2ax,b2+y2≥2by,两式相加即可得到.
(3)已知a2+b2=1,x2+y2=1,求证:ax+by≤1.
(2)已知a,b,c为正实数,求证: ≥abc;
新知探究
方法总结:利用均值不等式证明不等式的两种题型:(1)无附加条件的不等式的证明.其解题思路:观察待证不等式的结构形式,若不能直接使用均值不等式,则结合左、右两边的结构特征,进行拆项、变形、配凑等,使之达到使用均值不等式的条件.(2)有附加条件的不等式的证明.观察已知条件与待证不等式之间的关系,恰当地使用已知条件,条件的巧妙代换是一种较为重要的变形.
新知探究
【探索与研究】用Excel或其他计算机软件,完成下列数学实验:
(1)任取多组三个正教a,b,c,计算 和 运后,比较它们的大小,总结出一般规律;
(2)对四个正数、五个正数做同样的实验,总结出普遍规律.
一般地, ,当且仅当a1=a2=…=an时,等号成立.
归纳小结
回顾本节课,你有什么收获?
(1)均值不等式有哪些变形?如何证明?
(2)如何利用均值不等式及其变形证明不等式?
利用均值不等式证明不等式的注意点:
(1)多次使用均值不等式时,要注意等号能否成立.
(2)累加法是不等式证明中的一种常用方法,证明不等式时注意使用.
(3)对不能直接使用均值不等式的证明可重新组合,达到使用均值不等式的条件.
作业:教科书P76练习B 3.
作业布置
作业布置
已知a>0,b>0,a+b=1,求证:(1+ )(1+ )≥9.
补
因为a>0,b>0,a+b=1,
所以
同理
故
所以 ,当且仅当a=b= 时取等号.
再见
