第三章 圆 综合能力检测卷(含解析)
图片预览



文档简介
北师大版数学九年级下册 第三章 圆 综合能力检测卷
一、选择题(本大题共10小题,每题3分,共30分)
1.下列说法中,正确的是 ( )
A.两点确定一个圆
B.度数相等的弧相等
C.垂直于弦的直径平分弦
D.相等的圆周角所对的弧相等,所对的弦也相等
2.如图,一块直角三角形纸板ABC的斜边AB与量角器的直径重合,点D对应54°,则∠BCD的度数为 ( )
A.27° B.54° C.36° D.63°
3.已知☉O的半径是5cm,点O到直线l的距离OP=3cm,Q为l上一点,且PQ=4.2cm,则点Q ( )
A.在☉O内 B.在☉O上
C.在☉O外 D.以上情况都有可能
4.如图,在正三角形网格中,△ABC的顶点都在格点上,点P,Q,M是AB与格线的交点,则△ABC的外心是 ( )
A.点P B.点Q
C.点M D.点N
第4题 第5题图 第6题图
5.一定滑轮的起重装置如图,滑轮半径为12cm,当重物上升4πcm时,滑轮的一条半径OA按逆时针方向旋转的度数为(假设绳索与滑轮之间没有滑动) ( )
A.12° B.30° C.60° D.90°
6.如图,在△ABC中,AB=6,AC=8,BC=10,D,E分别是AC,AB的中点,则以DE为直径的圆与BC的位置关系是 ( )
A.相交 B.相切 C.相离 D.无法确定
7.有一种折叠式饭桌,将正方形桌面边上的四个弓形面板翻折起来后,就能形成一个圆形桌面(可近似看作正方形的外接圆),正方形桌面与翻折成的圆形桌面的面积之比最接近 ( )
A.45 B.34 C.23 D.12
8.如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,她了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25m,BD=1.5m,且AB,CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是 ( )
A.2m B.2.5m C.2.4m D.2.1m
第8题图 第9题图 第10题图
9.如图,圆心C在x轴上的半圆交x轴于A,B两点,交y轴于点D(0,3),M是BD上一点,且AD=MD.若BM=8,则点C的坐标为 ( )
A.(2,0) B.(3,0) C.(4,0) D.(5,0)
10.如图,☉O的半径为2,AB,CD是互相垂直的两条直径,点P是☉O上任意一点(P与A,B,C,D不重合),过点P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P沿着圆周转过45°时,点Q走过的路径长为 ( )
A.π4 B.π2 C.π6 D.π3
二、填空题(本大题共6小题,每题3分,共18分)
11.如图,AC是☉O的切线,切点为C,BC是☉O的直径,AB交☉O于点D,连接OD,若∠BAC=50°,则∠COD的大小为 .?
第11题 第13题图 第14题图
12.已知☉O的半径为2cm,弦AB长为23cm,则这条弦的中点到弦所对劣弧的中点的距离为 cm.?
13.如图,四边形ABCD是☉O的内接四边形,延长AD,BC相交于点E,延长AB,DC相交于点F.若∠E=∠F=40°,则∠A的度数为 .?
14.如图,以正方形ABCD的边AB为直径作半圆O,CE切半圆于点F,交AD边于点E,若△CDE的周长为12,则四边形ABCE的周长为 .?
15.如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为 .?
第15题 第16题图
16.如图,△OAC的顶点O在坐标原点,OA边在x轴上,OA=2,AC=1,把△OAC绕点A按顺时针方向旋转得到△O'AC',使得点O'的坐标是(1,3),则在旋转过程中线段OC扫过部分(阴影部分)的面积为 .?
三、解答题(本大题共6小题,共72分)
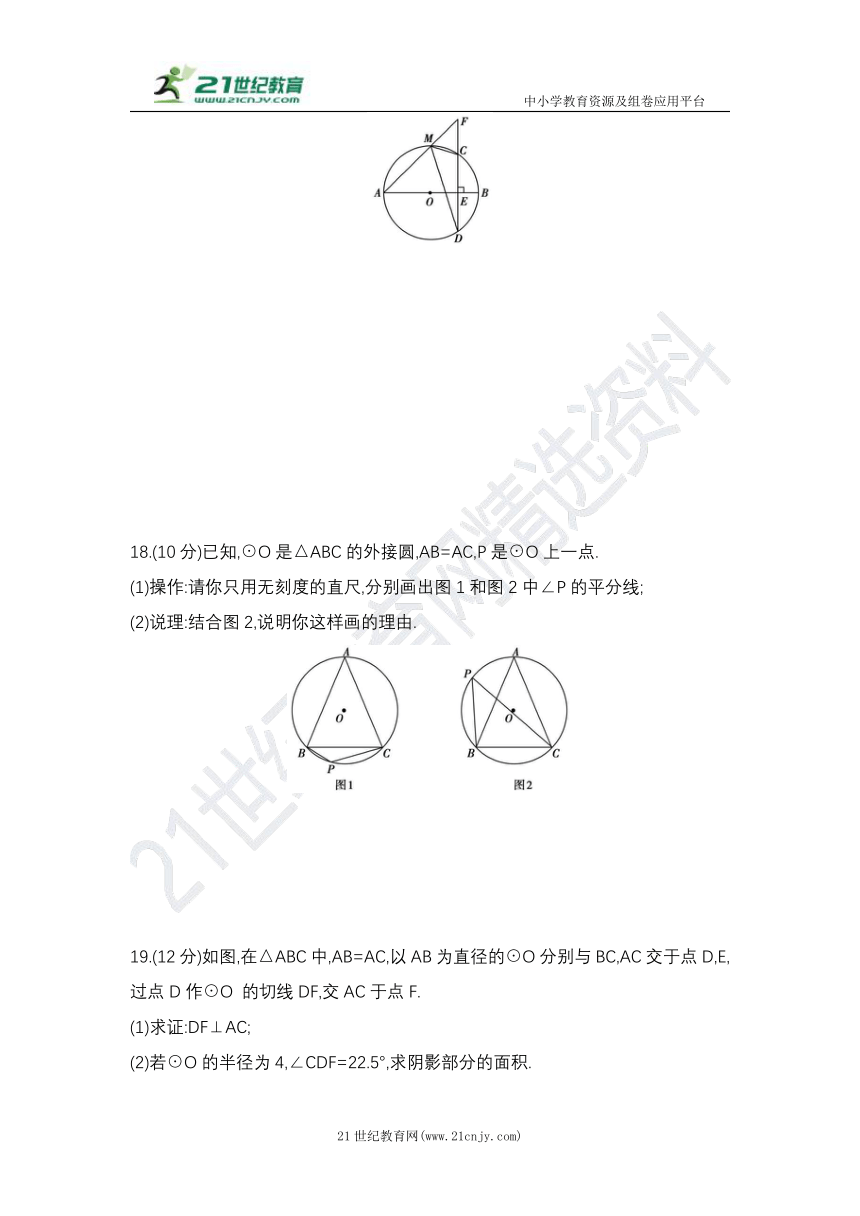
17.(10分)如图,已知AB是☉O的直径,CD为弦,且CD⊥AB于点E,F为DC延长线上的一点,连接AF交☉O于点M.求证:∠AMD=∠FMC.
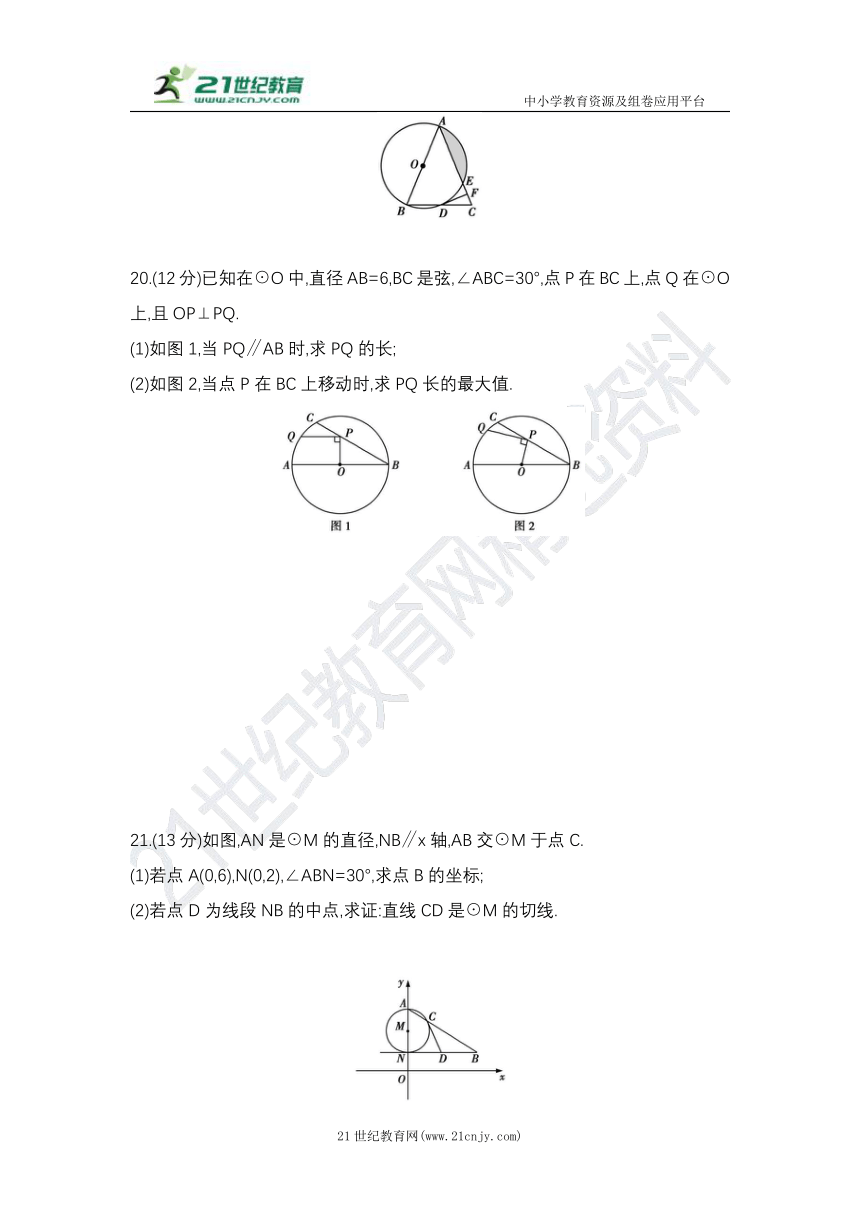
18.(10分)已知,☉O是△ABC的外接圆,AB=AC,P是☉O上一点.
(1)操作:请你只用无刻度的直尺,分别画出图1和图2中∠P的平分线;
(2)说理:结合图2,说明你这样画的理由.
19.(12分)如图,在△ABC中,AB=AC,以AB为直径的☉O分别与BC,AC交于点D,E,过点D作☉O 的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若☉O的半径为4,∠CDF=22.5°,求阴影部分的面积.
20.(12分)已知在☉O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在☉O上,且OP⊥PQ.
(1)如图1,当PQ∥AB时,求PQ的长;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
21.(13分)如图,AN是☉M的直径,NB∥x轴,AB交☉M于点C.
(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;
(2)若点D为线段NB的中点,求证:直线CD是☉M的切线.
22.(15分)如图,AB是☉O的直径,AD,BD是弦,且∠PDA=∠PBD.延长PD交☉O的切线BE于点E.
(1)判断直线PD是否为☉O的切线,并说明理由;
(2)如果∠BED=60°,PD=3,求PA的长;
(3)将线段PD以直线AD为对称轴作对称线段DF,点F正好在☉O上,求证:四边形DFBE为菱形.
参考答案与解析
1.C 【解析】 不在同一条直线上的三点确定一个圆,故A错误;在同圆或等圆中,能够互相重合的弧叫做等弧,故B错误;根据垂径定理,知C正确;在同圆或等圆中,相等的圆周角所对的弧相等,所对的弦也相等,故D错误.故选C.
2.D 【解析】 连接OD.∵一块直角三角形纸板ABC的斜边AB与量角器的直径重合,∴点A,B,C,D都在以O为圆心、AB为直径的圆上,∵点D对应54°,即∠AOD=54°,∴∠ACD=12∠AOD=27°,∴∠BCD=90°-∠ACD=63°.故选D.
3.C 【解析】 由垂径定理知,点P是直线l被☉O截得的弦的中点,如图,OP⊥PA,OP=3cm,OA=5cm,
∴PA=OA2-OP2=4cm,∵4.2cm>4cm,∴点Q在☉O外.故选C.
4.B 【解析】 由题意可知,∠BCN=60°,∠ACN=30°,∴∠ACB=∠ACN+∠BCN=90°,∴△ABC是直角三角形,∴△ABC的外心是斜边AB的中点,由题图易知点Q是AB的中点,∴△ABC的外心是点Q.故选B.
5.C 【解析】 由于重物上升的高度为4πcm,所以旋转角所对的弧长为4πcm,设旋转角的度数为n°,由弧长公式得nπ×12180=4π,所以n=60.故选C.
6.A 【解析】 如图,过点A作AM⊥BC于点M,交DE于点N,∵AB=6,AC=8,BC=10,∴AB2+AC2=BC2,∴∠BAC=90°.在Rt△ABC中,AM·BC=AC·AB,∴AM=6×810=4.8.∵D,E分别是AC,AB的中点,∴DE∥BC,DE=12BC=5,∴AN=MN=12AM=2.4.
∵以DE为直径的圆半径为2.5,2.5>2.4,∴以DE为直径的圆与BC的位置关系是相交.故选A.
7.C 【解析】 如图,连接AC,设正方形的边长为a,∵四边形ABCD是正方形,∴∠B=90°,∴AC为正方形ABCD外接圆的直径,AC=2AB=2a,则正方形桌面与翻折成的圆形桌面的面积之比为a2π×(22a)2=2π≈23.故选C.
8.B 【解析】 如图,设圆弧形门所在圆的圆心为O,BD的中点为点F,连接OA,AC,OF,OF交AC于点E,∵圆弧形门所在圆与水平地面相切,∴OF⊥BD.∵四边形ABDC是矩形,∴AC∥BD,∴OE⊥AC,EF=AB.设圆O的半径为Rm,在Rt△AOE中,AE=AC2=BD2=0.75m,OE=R-AB=(R-0.25)m,∵AE2+OE2=OA2,∴0.752+(R-0.25)2=R2,解得R=1.25.∴最高点离地面的距离为1.25×2=2.5(m).故选B.
在运用垂径定理解题的过程中,常作的辅助线是半径或弦心距,由此构造出运用垂径定理的条件,再结合勾股定理进行有关计算.
9.C 【解析】 如图,将半圆补成整圆,连接AM,CD,∵AB是☉C的直径,∴∠M=90°,设☉C与y轴负半轴的交点为点E,则AD=AE,OD=OE.∵AD=MD,∴DE=AM,∴AM=DE.∵OD=3,∴DE=6,∴AM=6.∵BM=8,∴AB=10,∴CD=5.在Rt△COD中,OC=CD2-OD2=4,∴点C的坐标为(4,0).故选C.
10.A 【解析】 连接OP,由题意知四边形OMPN是矩形,Q是其对角线MN与OP的交点,OQ=12OP=1,当点P沿着圆周转过45°时,点Q走过的路径长为以O为圆心、1为半径、圆心角为45°的扇形的弧长,∴点Q走过的路径长为45π180=π4.故选A.
11.80° 【解析】 ∵AC是☉O的切线,∴BC⊥AC,∴∠C=90°,∵∠BAC=50°,∴∠B=90°-∠BAC=40°,
∴∠COD=2∠B=80°.
12.1 【解析】 如图,E为AB的中点,F为劣弧AB的中点,连接OA,OB,OE,OF,易知O,E,F三点共线,且OE⊥AB,则AE=EB=12AB=3cm.在Rt△OEB中,OB=2cm,EB=3cm,∴OE=OB2-EB2=22-(3)2=1(cm),∴EF=OF-OE=2-1=1(cm),∴这条弦的中点到弦所对劣弧的中点的距离为1cm.
13.50° 【解析】 在△ABE与△ADF中,∠A为公共角,且∠E=∠F,由三角形内角和定理可知,∠ABE=∠ADF.
∵∠ABE与∠ADF是☉O的内接四边形的对角,∴∠ABE+∠ADF=180°,∴∠ABE=∠ADF=90°,∴∠A+∠E=90°,
∴∠A=90°-∠E=50°.
14.14 【解析】 设AE的长为x,易知AD,BC分别与半圆O相切于点A,B,∵CE与半圆O相切于点F,∴AE=EF,
BC=CF,∵EF+FC+CD+ED=12,∴AE+ED+CD+BC=12,即AD+CD+BC=12,∴正方形ABCD的边长为4.在Rt△CDE中,
ED2+CD2=CE2,即(4-x)2+42=(4+x)2,解得x=1,即AE的长为1.∴AE+EF+FC+BC+AB=14,∴四边形ABCE的周长为14.
15.88° 【解析】 如图,∵AB=AC=AD,∴点B,C,D在以点A为圆心、AB的长为半径的圆上.∵∠CBD=2∠BDC,
∠CAD=2∠CBD,∠BAC=2∠BDC,∴∠CAD=2∠BAC,又∵∠BAC=44°,∴∠CAD=88°.
16.π2 【解析】 如图,过O'作O'M⊥OA于M,则∠O'MA=90°,∵点O'的坐标是(1,3),∴O'M=3,OM=1.
∵AO=2,∴AM=2-1=1,∴tan∠O'AM=31=3,∴∠O'AM=60°,即旋转角为60°,∴∠CAC'=∠OAO'=60°.∵把△OAC绕点A按顺时针方向旋转得到△O'AC',∴S△OAC=S△O'AC',∴阴影部分的面积S=S扇形OAO'+S△O'AC'-S△OAC-S扇形CAC'=S扇形OAO'-S扇形CAC'=60π×22360-60π×12360=π2.
17.【解析】 连接BC,BD.
∵∠CBA+∠AMC=180°,∠AMC+∠FMC=180°,
∴∠CBA=∠FMC.
∵CD⊥AB,AB为☉O的直径,
∴AC=AD,∴∠CBA=∠AMD.
∴∠AMD=∠FMC.
18.【解析】 (1)如图1,PA即∠BPC的平分线;
如图2,PE即∠BPC的平分线.
(2)如图2.
∵AB=AC,
∴AE是BC的垂直平分线,∴BE=CE,
∴∠BPE=∠CPE,即PE是∠BPC的平分线.
19.【解析】 (1)如图,连接OD,
∵OB=OD,∴∠ABC=∠ODB.
∵AB=AC,∴∠ABC=∠ACB.
∴∠ODB=∠ACB,∴OD∥AC.
∵DF是☉O的切线,∴DF⊥OD,
∴DF⊥AC.
(2)如图,连接OE.
∵DF⊥AC,∠CDF=22.5°,
∴∠ABC=∠ACB=67.5°,∴∠BAC=45°.
∵OA=OE,∴∠OEA=45°,∴∠AOE=90°.
∵☉O的半径为4,
∴S阴影=S扇形AOE-S△AOE=90π×42360-12×4×4=4π-8.
20.【解析】 (1)如图1,连接OQ.
∵PQ∥AB,OP⊥PQ,∴OP⊥AB.
在Rt△OBP中,∠ABC=30°,∴PB=2OP,
∵OB=3,PB2-OP2=OB2,∴3OP2=9,OP=3.
在Rt△OPQ中,OP=3,OQ=3,
∴PQ=OQ2-OP2=6.
(2)如图2,连接OQ,
在Rt△OPQ中,PQ=OQ2-OP2=9-OP2,
∴当OP的长最小时,PQ的长最大,
此时OP⊥BC,则OP=12OB=32,
∴PQ长的最大值为9-(32)2=332.
图1 图2
21.【解析】 (1)∵NB∥x轴,∴∠ANB=90°,点B的纵坐标为2.
∵A(0,6),N(0,2),∴☉M的直径AN=4,
又∵∠ABN=30°,∴AB=2AN=8.
在Rt△ANB中,由勾股定理,得AN2+BN2=AB2,
即42+BN2=82,∴BN=43,即点B的横坐标为43,
∴点B的坐标为(43,2).
(2)如图,连接NC,CM,DM.
∵AN为☉M的直径,∴∠ACN=∠BCN=90°.
在Rt△BCN中,点D为NB的中点,∴CD=12BN=DN.
∵CM=NM,DM=DM,∴△DCM≌△DNM,
∴∠MCD=∠MND=90°,∴MC⊥CD.
又∵点C在☉M上,∴直线CD是☉M的切线.
22.【解析】 (1)直线PD是☉O的切线.理由如下:
如图,连接OD,∵AB是圆O的直径,∴∠ADB=90°,
∴∠ADO+∠BDO=90°,
又∵DO=BO,∴∠BDO=∠PBD.
∵∠PDA=∠PBD,∴∠BDO=∠PDA,
∴∠ADO+∠PDA=90°,即PD⊥OD.
∵点D在☉O上,∴直线PD为☉O的切线.
(2)∵BE是☉O的切线,∴∠EBA=90°.
∵∠BED=60°,∴∠P=30°.
∵PD为☉O的切线,∴∠PDO=90°.
在Rt△PDO中,∠P=30°,PD=3,
∴PO=2DO,根据勾股定理,得OD2+(3)2=(2OD)2,
∴OD=1,∴OA=OD=1,PO=2OD=2,∴PA=PO-OA=1.
(3)解法一 如图,连接AF,依题意得∠ADF=∠PDA,∠PAD=∠DAF,
∵∠PDA=∠PBD,∠ADF=∠ABF,
∴∠ADF=∠PDA=∠PBD=∠ABF.
∵AB是☉O的直径,∴∠ADB=90°.
设∠PBD=x°,则∠DAF=∠PAD=90°+x°,∠DBF=2x°.
∵四边形AFBD内接于☉O,∴∠DAF+∠DBF=180°,
即90°+x°+2x°=180°,解得x=30,
∴∠ADF=∠PDA=∠PBD=∠ABF=30°.
∵BE,ED是☉O的切线,∴DE=BE,∠EBA=90°,
∴∠DBE=60°,∴△BDE是等边三角形.
∴BD=DE=BE.
∵∠FDB=∠ADB-∠ADF=90°-30°=60°,∠DBF=∠PBD+∠ABF=60°,
∴△BDF是等边三角形,∴BD=DF=BF,
∴DE=BE=DF=BF,∴四边形DFBE为菱形.
解法二 如图,连接AF,依题意得∠ADF=∠PDA,∠APD=∠AFD,
∵∠PDA=∠PBD,∠ADF=∠ABF,∠PAD=∠DAF,
∴∠ADF=∠AFD=∠BPD=∠ABF,
∴AD=AF,BF∥PD,∴DF⊥PB.
∵BE为切线,∴BE⊥PB,∴DF∥BE,
∴四边形DFBE为平行四边形.
∵PE,BE为切线,∴BE=DE,
∴?DFBE为菱形.
一、选择题(本大题共10小题,每题3分,共30分)
1.下列说法中,正确的是 ( )
A.两点确定一个圆
B.度数相等的弧相等
C.垂直于弦的直径平分弦
D.相等的圆周角所对的弧相等,所对的弦也相等
2.如图,一块直角三角形纸板ABC的斜边AB与量角器的直径重合,点D对应54°,则∠BCD的度数为 ( )
A.27° B.54° C.36° D.63°
3.已知☉O的半径是5cm,点O到直线l的距离OP=3cm,Q为l上一点,且PQ=4.2cm,则点Q ( )
A.在☉O内 B.在☉O上
C.在☉O外 D.以上情况都有可能
4.如图,在正三角形网格中,△ABC的顶点都在格点上,点P,Q,M是AB与格线的交点,则△ABC的外心是 ( )
A.点P B.点Q
C.点M D.点N
第4题 第5题图 第6题图
5.一定滑轮的起重装置如图,滑轮半径为12cm,当重物上升4πcm时,滑轮的一条半径OA按逆时针方向旋转的度数为(假设绳索与滑轮之间没有滑动) ( )
A.12° B.30° C.60° D.90°
6.如图,在△ABC中,AB=6,AC=8,BC=10,D,E分别是AC,AB的中点,则以DE为直径的圆与BC的位置关系是 ( )
A.相交 B.相切 C.相离 D.无法确定
7.有一种折叠式饭桌,将正方形桌面边上的四个弓形面板翻折起来后,就能形成一个圆形桌面(可近似看作正方形的外接圆),正方形桌面与翻折成的圆形桌面的面积之比最接近 ( )
A.45 B.34 C.23 D.12
8.如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,她了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25m,BD=1.5m,且AB,CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是 ( )
A.2m B.2.5m C.2.4m D.2.1m
第8题图 第9题图 第10题图
9.如图,圆心C在x轴上的半圆交x轴于A,B两点,交y轴于点D(0,3),M是BD上一点,且AD=MD.若BM=8,则点C的坐标为 ( )
A.(2,0) B.(3,0) C.(4,0) D.(5,0)
10.如图,☉O的半径为2,AB,CD是互相垂直的两条直径,点P是☉O上任意一点(P与A,B,C,D不重合),过点P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P沿着圆周转过45°时,点Q走过的路径长为 ( )
A.π4 B.π2 C.π6 D.π3
二、填空题(本大题共6小题,每题3分,共18分)
11.如图,AC是☉O的切线,切点为C,BC是☉O的直径,AB交☉O于点D,连接OD,若∠BAC=50°,则∠COD的大小为 .?
第11题 第13题图 第14题图
12.已知☉O的半径为2cm,弦AB长为23cm,则这条弦的中点到弦所对劣弧的中点的距离为 cm.?
13.如图,四边形ABCD是☉O的内接四边形,延长AD,BC相交于点E,延长AB,DC相交于点F.若∠E=∠F=40°,则∠A的度数为 .?
14.如图,以正方形ABCD的边AB为直径作半圆O,CE切半圆于点F,交AD边于点E,若△CDE的周长为12,则四边形ABCE的周长为 .?
15.如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为 .?
第15题 第16题图
16.如图,△OAC的顶点O在坐标原点,OA边在x轴上,OA=2,AC=1,把△OAC绕点A按顺时针方向旋转得到△O'AC',使得点O'的坐标是(1,3),则在旋转过程中线段OC扫过部分(阴影部分)的面积为 .?
三、解答题(本大题共6小题,共72分)
17.(10分)如图,已知AB是☉O的直径,CD为弦,且CD⊥AB于点E,F为DC延长线上的一点,连接AF交☉O于点M.求证:∠AMD=∠FMC.
18.(10分)已知,☉O是△ABC的外接圆,AB=AC,P是☉O上一点.
(1)操作:请你只用无刻度的直尺,分别画出图1和图2中∠P的平分线;
(2)说理:结合图2,说明你这样画的理由.
19.(12分)如图,在△ABC中,AB=AC,以AB为直径的☉O分别与BC,AC交于点D,E,过点D作☉O 的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若☉O的半径为4,∠CDF=22.5°,求阴影部分的面积.
20.(12分)已知在☉O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在☉O上,且OP⊥PQ.
(1)如图1,当PQ∥AB时,求PQ的长;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
21.(13分)如图,AN是☉M的直径,NB∥x轴,AB交☉M于点C.
(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;
(2)若点D为线段NB的中点,求证:直线CD是☉M的切线.
22.(15分)如图,AB是☉O的直径,AD,BD是弦,且∠PDA=∠PBD.延长PD交☉O的切线BE于点E.
(1)判断直线PD是否为☉O的切线,并说明理由;
(2)如果∠BED=60°,PD=3,求PA的长;
(3)将线段PD以直线AD为对称轴作对称线段DF,点F正好在☉O上,求证:四边形DFBE为菱形.
参考答案与解析
1.C 【解析】 不在同一条直线上的三点确定一个圆,故A错误;在同圆或等圆中,能够互相重合的弧叫做等弧,故B错误;根据垂径定理,知C正确;在同圆或等圆中,相等的圆周角所对的弧相等,所对的弦也相等,故D错误.故选C.
2.D 【解析】 连接OD.∵一块直角三角形纸板ABC的斜边AB与量角器的直径重合,∴点A,B,C,D都在以O为圆心、AB为直径的圆上,∵点D对应54°,即∠AOD=54°,∴∠ACD=12∠AOD=27°,∴∠BCD=90°-∠ACD=63°.故选D.
3.C 【解析】 由垂径定理知,点P是直线l被☉O截得的弦的中点,如图,OP⊥PA,OP=3cm,OA=5cm,
∴PA=OA2-OP2=4cm,∵4.2cm>4cm,∴点Q在☉O外.故选C.
4.B 【解析】 由题意可知,∠BCN=60°,∠ACN=30°,∴∠ACB=∠ACN+∠BCN=90°,∴△ABC是直角三角形,∴△ABC的外心是斜边AB的中点,由题图易知点Q是AB的中点,∴△ABC的外心是点Q.故选B.
5.C 【解析】 由于重物上升的高度为4πcm,所以旋转角所对的弧长为4πcm,设旋转角的度数为n°,由弧长公式得nπ×12180=4π,所以n=60.故选C.
6.A 【解析】 如图,过点A作AM⊥BC于点M,交DE于点N,∵AB=6,AC=8,BC=10,∴AB2+AC2=BC2,∴∠BAC=90°.在Rt△ABC中,AM·BC=AC·AB,∴AM=6×810=4.8.∵D,E分别是AC,AB的中点,∴DE∥BC,DE=12BC=5,∴AN=MN=12AM=2.4.
∵以DE为直径的圆半径为2.5,2.5>2.4,∴以DE为直径的圆与BC的位置关系是相交.故选A.
7.C 【解析】 如图,连接AC,设正方形的边长为a,∵四边形ABCD是正方形,∴∠B=90°,∴AC为正方形ABCD外接圆的直径,AC=2AB=2a,则正方形桌面与翻折成的圆形桌面的面积之比为a2π×(22a)2=2π≈23.故选C.
8.B 【解析】 如图,设圆弧形门所在圆的圆心为O,BD的中点为点F,连接OA,AC,OF,OF交AC于点E,∵圆弧形门所在圆与水平地面相切,∴OF⊥BD.∵四边形ABDC是矩形,∴AC∥BD,∴OE⊥AC,EF=AB.设圆O的半径为Rm,在Rt△AOE中,AE=AC2=BD2=0.75m,OE=R-AB=(R-0.25)m,∵AE2+OE2=OA2,∴0.752+(R-0.25)2=R2,解得R=1.25.∴最高点离地面的距离为1.25×2=2.5(m).故选B.
在运用垂径定理解题的过程中,常作的辅助线是半径或弦心距,由此构造出运用垂径定理的条件,再结合勾股定理进行有关计算.
9.C 【解析】 如图,将半圆补成整圆,连接AM,CD,∵AB是☉C的直径,∴∠M=90°,设☉C与y轴负半轴的交点为点E,则AD=AE,OD=OE.∵AD=MD,∴DE=AM,∴AM=DE.∵OD=3,∴DE=6,∴AM=6.∵BM=8,∴AB=10,∴CD=5.在Rt△COD中,OC=CD2-OD2=4,∴点C的坐标为(4,0).故选C.
10.A 【解析】 连接OP,由题意知四边形OMPN是矩形,Q是其对角线MN与OP的交点,OQ=12OP=1,当点P沿着圆周转过45°时,点Q走过的路径长为以O为圆心、1为半径、圆心角为45°的扇形的弧长,∴点Q走过的路径长为45π180=π4.故选A.
11.80° 【解析】 ∵AC是☉O的切线,∴BC⊥AC,∴∠C=90°,∵∠BAC=50°,∴∠B=90°-∠BAC=40°,
∴∠COD=2∠B=80°.
12.1 【解析】 如图,E为AB的中点,F为劣弧AB的中点,连接OA,OB,OE,OF,易知O,E,F三点共线,且OE⊥AB,则AE=EB=12AB=3cm.在Rt△OEB中,OB=2cm,EB=3cm,∴OE=OB2-EB2=22-(3)2=1(cm),∴EF=OF-OE=2-1=1(cm),∴这条弦的中点到弦所对劣弧的中点的距离为1cm.
13.50° 【解析】 在△ABE与△ADF中,∠A为公共角,且∠E=∠F,由三角形内角和定理可知,∠ABE=∠ADF.
∵∠ABE与∠ADF是☉O的内接四边形的对角,∴∠ABE+∠ADF=180°,∴∠ABE=∠ADF=90°,∴∠A+∠E=90°,
∴∠A=90°-∠E=50°.
14.14 【解析】 设AE的长为x,易知AD,BC分别与半圆O相切于点A,B,∵CE与半圆O相切于点F,∴AE=EF,
BC=CF,∵EF+FC+CD+ED=12,∴AE+ED+CD+BC=12,即AD+CD+BC=12,∴正方形ABCD的边长为4.在Rt△CDE中,
ED2+CD2=CE2,即(4-x)2+42=(4+x)2,解得x=1,即AE的长为1.∴AE+EF+FC+BC+AB=14,∴四边形ABCE的周长为14.
15.88° 【解析】 如图,∵AB=AC=AD,∴点B,C,D在以点A为圆心、AB的长为半径的圆上.∵∠CBD=2∠BDC,
∠CAD=2∠CBD,∠BAC=2∠BDC,∴∠CAD=2∠BAC,又∵∠BAC=44°,∴∠CAD=88°.
16.π2 【解析】 如图,过O'作O'M⊥OA于M,则∠O'MA=90°,∵点O'的坐标是(1,3),∴O'M=3,OM=1.
∵AO=2,∴AM=2-1=1,∴tan∠O'AM=31=3,∴∠O'AM=60°,即旋转角为60°,∴∠CAC'=∠OAO'=60°.∵把△OAC绕点A按顺时针方向旋转得到△O'AC',∴S△OAC=S△O'AC',∴阴影部分的面积S=S扇形OAO'+S△O'AC'-S△OAC-S扇形CAC'=S扇形OAO'-S扇形CAC'=60π×22360-60π×12360=π2.
17.【解析】 连接BC,BD.
∵∠CBA+∠AMC=180°,∠AMC+∠FMC=180°,
∴∠CBA=∠FMC.
∵CD⊥AB,AB为☉O的直径,
∴AC=AD,∴∠CBA=∠AMD.
∴∠AMD=∠FMC.
18.【解析】 (1)如图1,PA即∠BPC的平分线;
如图2,PE即∠BPC的平分线.
(2)如图2.
∵AB=AC,
∴AE是BC的垂直平分线,∴BE=CE,
∴∠BPE=∠CPE,即PE是∠BPC的平分线.
19.【解析】 (1)如图,连接OD,
∵OB=OD,∴∠ABC=∠ODB.
∵AB=AC,∴∠ABC=∠ACB.
∴∠ODB=∠ACB,∴OD∥AC.
∵DF是☉O的切线,∴DF⊥OD,
∴DF⊥AC.
(2)如图,连接OE.
∵DF⊥AC,∠CDF=22.5°,
∴∠ABC=∠ACB=67.5°,∴∠BAC=45°.
∵OA=OE,∴∠OEA=45°,∴∠AOE=90°.
∵☉O的半径为4,
∴S阴影=S扇形AOE-S△AOE=90π×42360-12×4×4=4π-8.
20.【解析】 (1)如图1,连接OQ.
∵PQ∥AB,OP⊥PQ,∴OP⊥AB.
在Rt△OBP中,∠ABC=30°,∴PB=2OP,
∵OB=3,PB2-OP2=OB2,∴3OP2=9,OP=3.
在Rt△OPQ中,OP=3,OQ=3,
∴PQ=OQ2-OP2=6.
(2)如图2,连接OQ,
在Rt△OPQ中,PQ=OQ2-OP2=9-OP2,
∴当OP的长最小时,PQ的长最大,
此时OP⊥BC,则OP=12OB=32,
∴PQ长的最大值为9-(32)2=332.
图1 图2
21.【解析】 (1)∵NB∥x轴,∴∠ANB=90°,点B的纵坐标为2.
∵A(0,6),N(0,2),∴☉M的直径AN=4,
又∵∠ABN=30°,∴AB=2AN=8.
在Rt△ANB中,由勾股定理,得AN2+BN2=AB2,
即42+BN2=82,∴BN=43,即点B的横坐标为43,
∴点B的坐标为(43,2).
(2)如图,连接NC,CM,DM.
∵AN为☉M的直径,∴∠ACN=∠BCN=90°.
在Rt△BCN中,点D为NB的中点,∴CD=12BN=DN.
∵CM=NM,DM=DM,∴△DCM≌△DNM,
∴∠MCD=∠MND=90°,∴MC⊥CD.
又∵点C在☉M上,∴直线CD是☉M的切线.
22.【解析】 (1)直线PD是☉O的切线.理由如下:
如图,连接OD,∵AB是圆O的直径,∴∠ADB=90°,
∴∠ADO+∠BDO=90°,
又∵DO=BO,∴∠BDO=∠PBD.
∵∠PDA=∠PBD,∴∠BDO=∠PDA,
∴∠ADO+∠PDA=90°,即PD⊥OD.
∵点D在☉O上,∴直线PD为☉O的切线.
(2)∵BE是☉O的切线,∴∠EBA=90°.
∵∠BED=60°,∴∠P=30°.
∵PD为☉O的切线,∴∠PDO=90°.
在Rt△PDO中,∠P=30°,PD=3,
∴PO=2DO,根据勾股定理,得OD2+(3)2=(2OD)2,
∴OD=1,∴OA=OD=1,PO=2OD=2,∴PA=PO-OA=1.
(3)解法一 如图,连接AF,依题意得∠ADF=∠PDA,∠PAD=∠DAF,
∵∠PDA=∠PBD,∠ADF=∠ABF,
∴∠ADF=∠PDA=∠PBD=∠ABF.
∵AB是☉O的直径,∴∠ADB=90°.
设∠PBD=x°,则∠DAF=∠PAD=90°+x°,∠DBF=2x°.
∵四边形AFBD内接于☉O,∴∠DAF+∠DBF=180°,
即90°+x°+2x°=180°,解得x=30,
∴∠ADF=∠PDA=∠PBD=∠ABF=30°.
∵BE,ED是☉O的切线,∴DE=BE,∠EBA=90°,
∴∠DBE=60°,∴△BDE是等边三角形.
∴BD=DE=BE.
∵∠FDB=∠ADB-∠ADF=90°-30°=60°,∠DBF=∠PBD+∠ABF=60°,
∴△BDF是等边三角形,∴BD=DF=BF,
∴DE=BE=DF=BF,∴四边形DFBE为菱形.
解法二 如图,连接AF,依题意得∠ADF=∠PDA,∠APD=∠AFD,
∵∠PDA=∠PBD,∠ADF=∠ABF,∠PAD=∠DAF,
∴∠ADF=∠AFD=∠BPD=∠ABF,
∴AD=AF,BF∥PD,∴DF⊥PB.
∵BE为切线,∴BE⊥PB,∴DF∥BE,
∴四边形DFBE为平行四边形.
∵PE,BE为切线,∴BE=DE,
∴?DFBE为菱形.
