沪科版数学九年级下册期中综合检测卷(含解析)
文档属性
| 名称 | 沪科版数学九年级下册期中综合检测卷(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-04 00:00:00 | ||
图片预览





文档简介
沪科版数学九年级下册期中综合检测卷
一、选择题(每题4分,共40分)
1.下列现象不属于投影的是 ( )
A.树影 B.手影 C.素描画 D.皮影
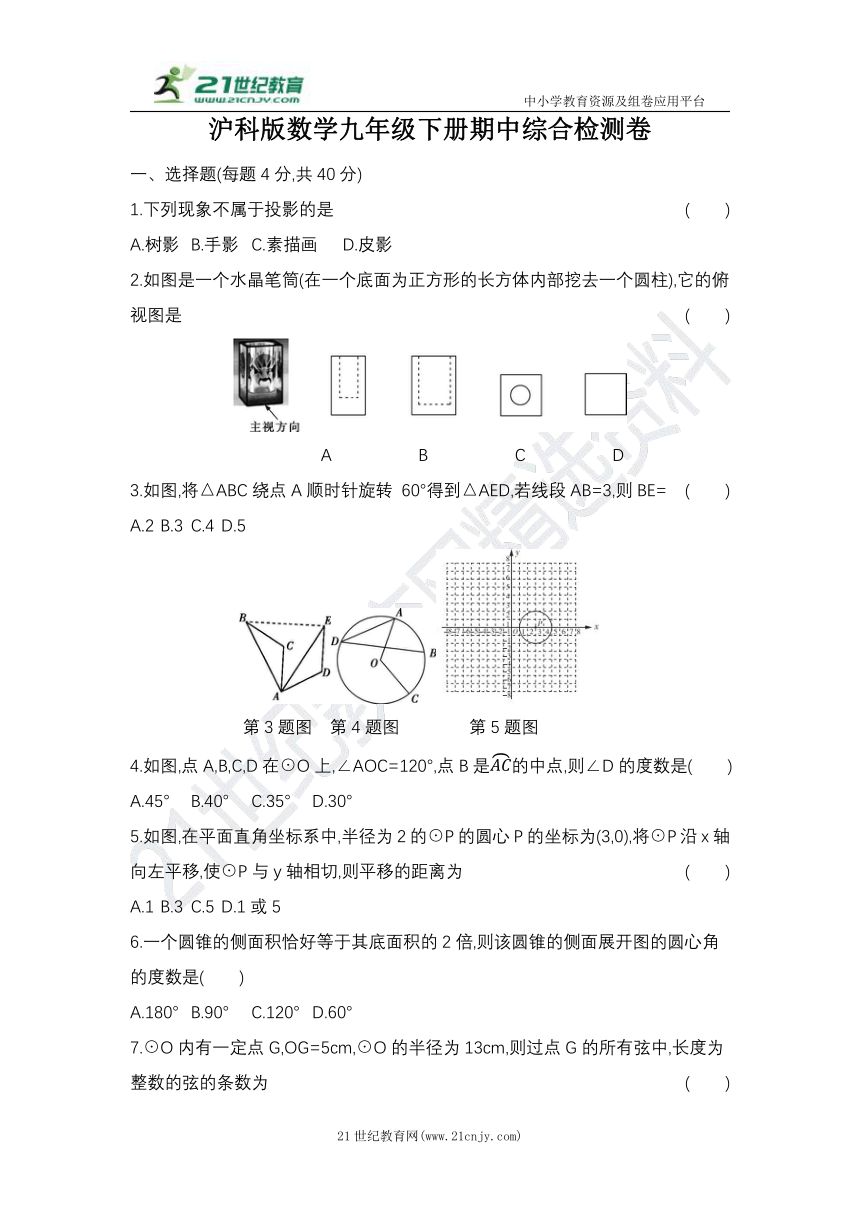
2.如图是一个水晶笔筒(在一个底面为正方形的长方体内部挖去一个圆柱),它的俯视图是 ( )
A B C D
3.如图,将△ABC绕点A顺时针旋转 60°得到△AED,若线段AB=3,则BE= ( )
A.2 B.3 C.4 D.5
第3题图 第4题图 第5题图
4.如图,点A,B,C,D在☉O上,∠AOC=120°,点B是AC的中点,则∠D的度数是 ( )
A.45° B.40° C.35° D.30°
5.如图,在平面直角坐标系中,半径为2的☉P的圆心P的坐标为(3,0),将☉P沿x轴向左平移,使☉P与y轴相切,则平移的距离为 ( )
A.1 B.3 C.5 D.1或5
6.一个圆锥的侧面积恰好等于其底面积的2倍,则该圆锥的侧面展开图的圆心角的度数是( )
A.180° B.90° C.120° D.60°
7.☉O内有一定点G,OG=5cm,☉O的半径为13cm,则过点G的所有弦中,长度为整数的弦的条数为 ( )
A.2 B.3 C.4 D.无数
8.图中有两张型号完全一样的折叠式饭桌,将正方形桌面边上的四个弓形面板翻折起来后,就能形成一个圆形桌面(可近似看作正方形的外接圆),正方形桌面与翻折成的圆形桌面的面积之比最接近 ( )
A.45 B.34 C.23 D.12
第8题图 第9题图
9.如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形EBF的半径为2,圆心角为60°,则图中阴影部分的面积是 ( )
A.2π3-3 B.2π3-32 C.π-32 D.π-3
10.如图,在等腰直角三角形ABC中,∠BAC=90°,AB=AC,BC=22,点D是AC边上一动点(不与A,C重合),连接BD,与以AD为直径的圆交于点E,则线段CE长度的最小值为 ( )
A.22-2 B.5-1 C.5-2 D.3-1
二、填空题(每题5分,共20分)
11.为了测量水塔的高度,我们取一竹竿,放在阳光下,已知2米长的竹竿投影长为1.5米,在同一时刻测得水塔的投影长为30米,则水塔高为 米.?
12.如图,正方形ABCD的边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过A作半圆的切线,与半圆相切于点F,与DC相交于点E,则△ADE的面积为 cm2.?
第12题图 第13题图 第14题图
13.如图是由一些完全相同的小正方体搭成的几何体的俯视图和左视图,若这个几何体最多有m个小正方体组成,最少有n个小正方体组成,则m+n= .?
14.如图,在Rt△ABC中,∠C=90°,∠A=30°,在AC边上取点O为圆心画圆,使☉O经过A,B两点,下列结论正确的是 .(填序号)?
①AO=2CO;②AO=BC;③以O为圆心,OC为半径的圆与AB相切;④延长BC交☉O于点D,则A,B,D是☉O的三等分点.
三、解答题(共90分)
15.(8分)如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(-2,-2),B(-4,-1),C(-4,-4).
(1)作出△ABC关于原点O成中心对称的△A1B1C1;
(2)作出点A关于x轴的对称点A'.若把点A'向右平移a个单位长度后落在△A1B1C1的内部(不包括顶点和边界),求a的取值范围.
16.(8分)如图,为了测量学校旗杆的高度,小东用长为4m的竹竿做测量工具.移动竹竿,使其顶端的影子与旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8m,与旗杆相距22m,求旗杆的高度.
17.(8分)如图,在△ABC中,以点C为旋转中心,将△ABC旋转到△A'B'C的位置,其中A',B'分别是A,B的对应点,且点B'在AB边上,按照上述方法再旋转△A'B'C……这样共旋转四次恰好构成一个如图所示的旋转对称图形.
334645015557500(1)求∠BCB'的度数;
(2)判断△BCB'的形状.
18.(8分)如图是一个几何体的主视图与俯视图,根据图中数据(单位:mm),求该几何体的表面积.(结果保留π)
34099507302500
19.(10分)如图,AB是☉O的直径,C是☉O外一点,AB=AC,连接BC,交☉O于点D,过点D作DE⊥AC,垂足为E.
(1)求证:DE与☉O相切.
(2)若∠B=30°,AB=4,则图中阴影部分的面积是多少?(结果保留根号和π)
20.(10分)如图,△ABC内接于☉O,AB是直径,☉O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF.
(1)判断AF与☉O的位置关系并说明理由;
(2)若☉O的半径为4,AF=3,求AC的长.
21.(12分)如图,AB是☉O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PE⊥AB,垂足为E,射线EP交AC于点F,交过点C的切线于点D.
(1)求证:DC=DP;
(2)若直径AB=12cm,∠CAB=30°,
①当E是半径OA的中点时,DC= cm;?
②当AE= cm时,以A,O,C,F为顶点的四边形是菱形.?
400050015875000
22.(12分)如图,在平面直角坐标系中,线段AB=10,点A在y轴上滑动,点B随着点A的运动在x轴上滑动(点A,B与O不重合),Rt△AOB的内切圆☉K分别与OA,OB,AB切于点E,F,P.
(1)在上述的运动过程中,Rt△AOB的周长、☉K的半径、△AOB的外接圆的半径,这几个量中不会发生变化的是哪个?请简要说明理由.
(2)当AE=4时,求☉K的半径.
(3)设Rt△AOB的面积为S,AE=a,试求S与a之间的函数表达式,并求出当S的值最大时,直角边OA的长.
分)定义:若一个圆内接四边形的两条对角线互相垂直,则称这个四边形为“圆美四边形”.
(1)请你写出一个你学过的特殊四边形中是“圆美四边形”的图形的名称: ;?
(2)如图1,在等腰直角三角形ABC中,∠BAC=90°,经过点A,B的圆交AC于点D,交BC于点E,连接DE,若四边形ABED为“圆美四边形”,求ABDE的值;
(3)如图2,在△ABC中,经过点A,B的圆交AC于点D,交BC于点E,连接AE,BD交于点F,若在四边形ABED的内部存在一点P,使得∠PBC=∠ADP=α,连接PE交BD于点G,连接PA,PB,若PA⊥PD,PB⊥PE.
①求证:四边形ABED为“圆美四边形”;
②若α=30°,PA+PE=8,CDBC=33,求DE的最小值.
参考答案与解析
1.C
2.C 【解析】 俯视图为正方形,且中间有圆.故选C.
3.B 【解析】 由旋转的性质可得AB=AE,∠BAE=60°,则△AEB是等边三角形,所以BE=AB=3.故选B.
4.D 【解析】 连接OB.因为点B是AC的中点,所以∠AOB=12∠AOC=60°,所以∠D=12∠AOB=30°.故选D.
5.D 【解析】 当☉P位于y轴的左侧且与y轴相切时,平移的距离为5;当☉P位于y轴的右侧且与y轴相切时,平移的距离为1.综上,平移的距离为1或5.故选D.
6.A 【解析】 设该圆锥的母线长为R,圆锥的侧面展开图的圆心角的度数为n,底面圆的半径为r,则底面圆的周长为2πr,底面圆的面积为πr2,该圆锥的侧面积为12×2πr×R=πRr=2×πr2,解得R=2r,所以nπR180°=2πr=πR,解得n=180°.故选A.
7.C 【解析】 如图所示,作AB⊥OG于点G,交☉O于A,B两点,则AG=BG,连接OA.在 Rt△AOG 中,OG=5,OA=13,∴AG=132-52=12,∴AB=24,故过点G的弦的长度在24和26之间,弦的长度为24的有1条,弦的长度为25的有2条,还有1条过点G的直径,∴过点G的弦中长度为整数的弦的条数为4.故选C.
27305010858500
8.C 【解析】 如图,连接AC,设正方形的边长为a.∵四边形ABCD是正方形,∴AC=2AB=2a,∵☉O是正方形ABCD的外接圆,∴AC为☉O的直径,则正方形桌面与翻折成的圆形桌面的面积之比为a2π×(22a)2=2π≈23.故选C.
6350006540500
A 【解析】 如图,连接BD,设AD,BE相交于点G,BF,DC相交于点H.∵四边形ABCD是菱
形,∠A=60°,∴△ABD 是等边三角形,∠1=∠2=60°,∴∠ABD=60°.又∵AB=2,∴△ABD的高为3.∵扇形EBF的圆心角为60°,∴∠4+∠5=60°,又∵∠3+∠5=60°,∴∠3=∠4.
在△ABG和△DBH中,
∴△ABG≌△DBH,∴S四边GBHD=S△ABD,∴S阴影=S扇形EBF-S△ABD=60π×22360-×2×3=2π3-3.故选A.
10.B 【解析】 如图1,连接AE,取AB的中点O,连接OE,OC.在等腰直角三角形ABC中,∠BAC=90°,AB=AC,BC=22,所以 AB=AC=2.因为AD为直径,所以∠AED=∠AEB=90°.在 Rt△AEB中,O为AB的中点,所以点E在以AB为直径的☉O上.当点O,E,C三点共线时,CE最小(如图2).在Rt△AOC中,OC=OA2+AC2=12+22=5,则CE的最小值为OC-OE=5-1.故选B.
11.40 【解析】 因为竹竿的高度∶竹竿的影长=水塔的高度∶水塔的影长,所以水塔的高度为21.5×30=40(米).
12.6 【解析】 ∵AE与☉O切于点F,∴由切线长定理得AF=AB=4cm,EF=EC,设EF=EC=xcm,则DE=(4-x)cm,AE=(4+x)cm,在Rt△ADE中,由勾股定理得(4-x)2+42=(4+x)2,∴x=1,即CE=1cm,∴DE=4-1=3(cm),∴S△ADE=12·AD·DE=12×4×3=6(cm2).
13.14 【解析】 根据几何体的左视图,可得这个几何体共有3层,从俯视图可以看出最底层的个数是4.(1)当第一层有1个小正方体,第二层有1个小正方体时,组成这个几何体的小正方体的个数是1+1+4=6;(2)当第一层有1个小正方体,第二层有2个小正方体时,组成这个几何体的小正方体的个数是1+2+4=7;(3)当第一层有2个小正方体,第二层有2个小正方体时,组成这个几何体的小正方体的个数是2+2+4=8.综上,可得组成这个几何体的小正方体的个数是6或7或8.所以m+n=8+6=14.
14.①③④ 【解析】 如图,连接OB,∵OA=OB,∴∠ABO=∠OAB=30°,∵∠ACB=90°,∴∠ABC=60°,∴∠OBC=30°,∴OC=12OB=12OA,即OA=2OC,故①正确;∵cos∠OBC=BCOB=32,∴BC=32OB,即BC=32OA,故②错误;∵∠ABO=∠OBC=30°,∴点O在∠ABC的平分线上,∴点O到直线AB的距离等于OC的长,∴以O为圆心,OC为半径的圆与AB相切,故③正确;如图,连接AD.∵AC⊥BD,∴DC=BC,∴AD=AB,又∵∠BAD=2∠BAC=60°,∴△ABD为等边三角形,∴AD=AB=BD,∴点A,B,D是☉O的三等分点,故④正确.结论正确的是①③④.
15.【解析】 (1)如图,△A1B1C1即为所求.
(2)点A'如图所示.
由图可知,a的取值范围是416.【解析】 设旗杆的高度为xm,
根据题意得48=x22+8,解得x=15,
即旗杆的高度为15m.
17.【解析】 (1)∵旋转四次恰好构成一个旋转对称图形,∴∠BCB'=360°÷5=72°.
(2)∵△A'B'C是由△ABC旋转得到的,
∴CB=CB',
∴△BCB'是等腰三角形.
18.【解析】 由三视图知该几何体是圆柱和长方体的组合体,
圆柱的底面直径为20mm,高为20mm,长方体的长、宽、高分别为30mm,25mm,40mm.
所以该几何体的表面积为(40×30+30×25+40×25)×2+π×(202)2+π×20×20-π×(202)2=5900+400π,
故该几何体的表面积是(5900+400π)mm2.
19.【解析】 (1)如图,连接OD.
∵AB=AC,OB=OD,∴∠B=∠C=∠ODB,∴OD∥AC,
∵DE⊥AC,∴∠CED=90°,∴∠ODE=90°,
又∵OD是☉O的半径,∴DE与☉O相切.
(2)如图,过点O作OF⊥BD于点F.
在Rt△OFB中,∠B=30°,OB=12AB=2,
∴OF=OB·sinB=1,BF=OB·cosB=3.
∴BD=2BF=23.
∵∠B=30°,∴∠AOD=60°.
阴影部分的面积为S△OBD+S扇形AOD=12×1×23+60π×22360=3+2π3.
20.【解析】 (1)AF是☉O的切线.理由如下:
连接OC,如图所示.
∵OF∥BC,∴∠1=∠2,∠B=∠3,
∵OC=OB,∴∠B=∠1,∴∠3=∠2,
在△OAF和△OCF中,OA=OC,∠3=∠2OF=OF,,∴△OAF≌△OCF(SAS),
∴∠OAF=∠OCF,
∵PC是☉O的切线,∴∠OCF=90°,
∴∠OAF=90°,∴FA⊥OA,
又∵OA是☉O的半径,∴AF是☉O的切线.
(2)∵AB是☉O的直径,∴∠BCA=90°,
∵OF∥BC,∴∠AEO=90°,即OF⊥AC.
∵☉O的半径为4,AF=3,∠OAF=90°,
∴OF=AF2+OA2=32+42=5,
∵FA⊥OA,OF⊥AC,∴AC=2AE,
△OAF的面积为12AF·OA=12OF·AE,
∴3×4=5×AE,解得AE=125,
∴AC=2AE=245.
21.【解析】 (1)如图,连接OC.
∵CD是☉O的切线,∴∠OCD=90°,
∵OA=OC,∴∠OAC=∠OCA,
∵PE⊥AB,∴∠PEA=90°,
∴∠OAC+∠APE=90°,∠OCA+∠PCD=90°,
∴∠APE=∠PCD,
∵∠APE=∠CPD,∴∠PCD=∠CPD,∴DC=DP.
(2)①43
如图,连接BC,
∵AB是直径,∴∠ACB=90°.
∵∠CAB=30°,AB=12,∴AC=AB·cos30°=63,
在Rt△APE中,∵AE=12OA=3,∴AP=AEcos30°=23,
∴PC=AC-AP=43,
∵∠APE=∠DPC=60°,DP=DC,∴△DPC是等边三角形,∴DC=43.
②3
当AE=EO=3时,四边形AOCF是菱形.理由如下:
如图,连接AF,OF.
∵AE=EO,FE⊥OA,∴FA=FO=OA,∴△AFO是等边三角形,∴∠FAO=60°,
∵∠CAB=30°,∴∠FAC=30°,∴∠FOC=2∠FAC=60°,
∴△FOC是等边三角形,∴CF=CO=OA=AF,∴四边形AOCF是菱形,
∴AE=3cm时,四边形AOCF是菱形.
22.【解析】 (1)不会发生变化的是△AOB的外接圆的半径.
理由如下:
∵∠AOB=90°,∴AB是△AOB的外接圆的直径,
∵AB=10,∴△AOB的外接圆的半径为5.
∴△AOB的外接圆的半径不变.
(2)如图,连接EK,KF.
则∠KEO=∠OFK=∠EOF=90°,
∴四边形EOFK是矩形.
又∵KE=KF,
∴四边形EOFK是正方形.
设☉K的半径为r,
则OE=OF=r,
∵AP=AE=4,AB=10,∴BF=PB=6.
∴在Rt△AOB中,有(4+r)2+(6+r)2=102,
解得r=2(负值已舍去),
故☉K的半径为2.
(3)在Rt△AOB中,OA2+OB2=AB2,
即(a+r)2+(10-a+r)2=102,
∴r2+10r=-a2+10a.
∴S=12r(OA+OB+AB)=12r(r+a+10-a+r+10)=r2+10r=-a2+10a=-(a-5)2+25,
∴当a=5时,S有最大值,此时AE=BF=5,
∴OA=OB=102=52.
23.【解析】 (1)正方形
(2)连接BD,AE.
∵∠BAC=90°,∴BD为四边形ABED的外接圆的直径,
∴∠BED=∠CED=90°.
∵四边形ABED为圆内接四边形,∴∠CDE=∠ABC,
∵∠ABC=∠C,∴∠EDC=∠C,
∴△DEC是等腰直角三角形.
∵四边形ABED为“圆美四边形”,∴BD⊥AE,∴AD=DE,
∴在等腰直角三角形CDE中,CD=2DE,∴CD=2AD,
∴AC=(2+1)AD,
∵AB=AC,AD=DE,∴ABDE=2+1.
(3)①∵PA⊥PD,PB⊥PE,∴∠APD=∠BPE=90°,
∵∠PBC=∠ADP,∴△APD∽△EPB,∴APPD=EPPB,
又∵∠APD+∠DPE=∠BPE+∠DPE,即∠APE=∠DPB,
∴△APE∽△DPB,∴∠AEP=∠DBP,
又∵∠DBP+∠PGB=90°,∠PGB=∠EGF,
∴∠AEP+∠EGF=90°,
∴∠BFE=90°,即BD⊥AE,
又∵A,B,E,D在同一个圆上,∴四边形ABED为“圆美四边形”.
②∵BD⊥AE,
∴AD2+BE2=AF2+FD2+BF2+EF2,AB2+DE2=AF2+BF2+DF2+EF2,
∴AD2+BE2=AB2+DE2,
∵A,B,E,D在同一个圆上,∴∠CDE=∠CBA,
∵∠C=∠C,∴△CDE∽△CBA,∴DEAB=CDBC=33,
设PA=x,DE=y,则PE=8-x,AB=3y,
∵α=30°,∠APD=∠BPE=90°,∴AD=2x,BE=2(8-x),
∴y2+(3y)2=(2x)2+[2(8-x)]2,
∴y2=x2+(8-x)2=2x2-16x+64=2(x-4)2+32,
∴当x=4时,y取到最小值42,即DE的最小值为42.
一、选择题(每题4分,共40分)
1.下列现象不属于投影的是 ( )
A.树影 B.手影 C.素描画 D.皮影
2.如图是一个水晶笔筒(在一个底面为正方形的长方体内部挖去一个圆柱),它的俯视图是 ( )
A B C D
3.如图,将△ABC绕点A顺时针旋转 60°得到△AED,若线段AB=3,则BE= ( )
A.2 B.3 C.4 D.5
第3题图 第4题图 第5题图
4.如图,点A,B,C,D在☉O上,∠AOC=120°,点B是AC的中点,则∠D的度数是 ( )
A.45° B.40° C.35° D.30°
5.如图,在平面直角坐标系中,半径为2的☉P的圆心P的坐标为(3,0),将☉P沿x轴向左平移,使☉P与y轴相切,则平移的距离为 ( )
A.1 B.3 C.5 D.1或5
6.一个圆锥的侧面积恰好等于其底面积的2倍,则该圆锥的侧面展开图的圆心角的度数是( )
A.180° B.90° C.120° D.60°
7.☉O内有一定点G,OG=5cm,☉O的半径为13cm,则过点G的所有弦中,长度为整数的弦的条数为 ( )
A.2 B.3 C.4 D.无数
8.图中有两张型号完全一样的折叠式饭桌,将正方形桌面边上的四个弓形面板翻折起来后,就能形成一个圆形桌面(可近似看作正方形的外接圆),正方形桌面与翻折成的圆形桌面的面积之比最接近 ( )
A.45 B.34 C.23 D.12
第8题图 第9题图
9.如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形EBF的半径为2,圆心角为60°,则图中阴影部分的面积是 ( )
A.2π3-3 B.2π3-32 C.π-32 D.π-3
10.如图,在等腰直角三角形ABC中,∠BAC=90°,AB=AC,BC=22,点D是AC边上一动点(不与A,C重合),连接BD,与以AD为直径的圆交于点E,则线段CE长度的最小值为 ( )
A.22-2 B.5-1 C.5-2 D.3-1
二、填空题(每题5分,共20分)
11.为了测量水塔的高度,我们取一竹竿,放在阳光下,已知2米长的竹竿投影长为1.5米,在同一时刻测得水塔的投影长为30米,则水塔高为 米.?
12.如图,正方形ABCD的边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过A作半圆的切线,与半圆相切于点F,与DC相交于点E,则△ADE的面积为 cm2.?
第12题图 第13题图 第14题图
13.如图是由一些完全相同的小正方体搭成的几何体的俯视图和左视图,若这个几何体最多有m个小正方体组成,最少有n个小正方体组成,则m+n= .?
14.如图,在Rt△ABC中,∠C=90°,∠A=30°,在AC边上取点O为圆心画圆,使☉O经过A,B两点,下列结论正确的是 .(填序号)?
①AO=2CO;②AO=BC;③以O为圆心,OC为半径的圆与AB相切;④延长BC交☉O于点D,则A,B,D是☉O的三等分点.
三、解答题(共90分)
15.(8分)如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(-2,-2),B(-4,-1),C(-4,-4).
(1)作出△ABC关于原点O成中心对称的△A1B1C1;
(2)作出点A关于x轴的对称点A'.若把点A'向右平移a个单位长度后落在△A1B1C1的内部(不包括顶点和边界),求a的取值范围.
16.(8分)如图,为了测量学校旗杆的高度,小东用长为4m的竹竿做测量工具.移动竹竿,使其顶端的影子与旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8m,与旗杆相距22m,求旗杆的高度.
17.(8分)如图,在△ABC中,以点C为旋转中心,将△ABC旋转到△A'B'C的位置,其中A',B'分别是A,B的对应点,且点B'在AB边上,按照上述方法再旋转△A'B'C……这样共旋转四次恰好构成一个如图所示的旋转对称图形.
334645015557500(1)求∠BCB'的度数;
(2)判断△BCB'的形状.
18.(8分)如图是一个几何体的主视图与俯视图,根据图中数据(单位:mm),求该几何体的表面积.(结果保留π)
34099507302500
19.(10分)如图,AB是☉O的直径,C是☉O外一点,AB=AC,连接BC,交☉O于点D,过点D作DE⊥AC,垂足为E.
(1)求证:DE与☉O相切.
(2)若∠B=30°,AB=4,则图中阴影部分的面积是多少?(结果保留根号和π)
20.(10分)如图,△ABC内接于☉O,AB是直径,☉O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF.
(1)判断AF与☉O的位置关系并说明理由;
(2)若☉O的半径为4,AF=3,求AC的长.
21.(12分)如图,AB是☉O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PE⊥AB,垂足为E,射线EP交AC于点F,交过点C的切线于点D.
(1)求证:DC=DP;
(2)若直径AB=12cm,∠CAB=30°,
①当E是半径OA的中点时,DC= cm;?
②当AE= cm时,以A,O,C,F为顶点的四边形是菱形.?
400050015875000
22.(12分)如图,在平面直角坐标系中,线段AB=10,点A在y轴上滑动,点B随着点A的运动在x轴上滑动(点A,B与O不重合),Rt△AOB的内切圆☉K分别与OA,OB,AB切于点E,F,P.
(1)在上述的运动过程中,Rt△AOB的周长、☉K的半径、△AOB的外接圆的半径,这几个量中不会发生变化的是哪个?请简要说明理由.
(2)当AE=4时,求☉K的半径.
(3)设Rt△AOB的面积为S,AE=a,试求S与a之间的函数表达式,并求出当S的值最大时,直角边OA的长.
分)定义:若一个圆内接四边形的两条对角线互相垂直,则称这个四边形为“圆美四边形”.
(1)请你写出一个你学过的特殊四边形中是“圆美四边形”的图形的名称: ;?
(2)如图1,在等腰直角三角形ABC中,∠BAC=90°,经过点A,B的圆交AC于点D,交BC于点E,连接DE,若四边形ABED为“圆美四边形”,求ABDE的值;
(3)如图2,在△ABC中,经过点A,B的圆交AC于点D,交BC于点E,连接AE,BD交于点F,若在四边形ABED的内部存在一点P,使得∠PBC=∠ADP=α,连接PE交BD于点G,连接PA,PB,若PA⊥PD,PB⊥PE.
①求证:四边形ABED为“圆美四边形”;
②若α=30°,PA+PE=8,CDBC=33,求DE的最小值.
参考答案与解析
1.C
2.C 【解析】 俯视图为正方形,且中间有圆.故选C.
3.B 【解析】 由旋转的性质可得AB=AE,∠BAE=60°,则△AEB是等边三角形,所以BE=AB=3.故选B.
4.D 【解析】 连接OB.因为点B是AC的中点,所以∠AOB=12∠AOC=60°,所以∠D=12∠AOB=30°.故选D.
5.D 【解析】 当☉P位于y轴的左侧且与y轴相切时,平移的距离为5;当☉P位于y轴的右侧且与y轴相切时,平移的距离为1.综上,平移的距离为1或5.故选D.
6.A 【解析】 设该圆锥的母线长为R,圆锥的侧面展开图的圆心角的度数为n,底面圆的半径为r,则底面圆的周长为2πr,底面圆的面积为πr2,该圆锥的侧面积为12×2πr×R=πRr=2×πr2,解得R=2r,所以nπR180°=2πr=πR,解得n=180°.故选A.
7.C 【解析】 如图所示,作AB⊥OG于点G,交☉O于A,B两点,则AG=BG,连接OA.在 Rt△AOG 中,OG=5,OA=13,∴AG=132-52=12,∴AB=24,故过点G的弦的长度在24和26之间,弦的长度为24的有1条,弦的长度为25的有2条,还有1条过点G的直径,∴过点G的弦中长度为整数的弦的条数为4.故选C.
27305010858500
8.C 【解析】 如图,连接AC,设正方形的边长为a.∵四边形ABCD是正方形,∴AC=2AB=2a,∵☉O是正方形ABCD的外接圆,∴AC为☉O的直径,则正方形桌面与翻折成的圆形桌面的面积之比为a2π×(22a)2=2π≈23.故选C.
6350006540500
A 【解析】 如图,连接BD,设AD,BE相交于点G,BF,DC相交于点H.∵四边形ABCD是菱
形,∠A=60°,∴△ABD 是等边三角形,∠1=∠2=60°,∴∠ABD=60°.又∵AB=2,∴△ABD的高为3.∵扇形EBF的圆心角为60°,∴∠4+∠5=60°,又∵∠3+∠5=60°,∴∠3=∠4.
在△ABG和△DBH中,
∴△ABG≌△DBH,∴S四边GBHD=S△ABD,∴S阴影=S扇形EBF-S△ABD=60π×22360-×2×3=2π3-3.故选A.
10.B 【解析】 如图1,连接AE,取AB的中点O,连接OE,OC.在等腰直角三角形ABC中,∠BAC=90°,AB=AC,BC=22,所以 AB=AC=2.因为AD为直径,所以∠AED=∠AEB=90°.在 Rt△AEB中,O为AB的中点,所以点E在以AB为直径的☉O上.当点O,E,C三点共线时,CE最小(如图2).在Rt△AOC中,OC=OA2+AC2=12+22=5,则CE的最小值为OC-OE=5-1.故选B.
11.40 【解析】 因为竹竿的高度∶竹竿的影长=水塔的高度∶水塔的影长,所以水塔的高度为21.5×30=40(米).
12.6 【解析】 ∵AE与☉O切于点F,∴由切线长定理得AF=AB=4cm,EF=EC,设EF=EC=xcm,则DE=(4-x)cm,AE=(4+x)cm,在Rt△ADE中,由勾股定理得(4-x)2+42=(4+x)2,∴x=1,即CE=1cm,∴DE=4-1=3(cm),∴S△ADE=12·AD·DE=12×4×3=6(cm2).
13.14 【解析】 根据几何体的左视图,可得这个几何体共有3层,从俯视图可以看出最底层的个数是4.(1)当第一层有1个小正方体,第二层有1个小正方体时,组成这个几何体的小正方体的个数是1+1+4=6;(2)当第一层有1个小正方体,第二层有2个小正方体时,组成这个几何体的小正方体的个数是1+2+4=7;(3)当第一层有2个小正方体,第二层有2个小正方体时,组成这个几何体的小正方体的个数是2+2+4=8.综上,可得组成这个几何体的小正方体的个数是6或7或8.所以m+n=8+6=14.
14.①③④ 【解析】 如图,连接OB,∵OA=OB,∴∠ABO=∠OAB=30°,∵∠ACB=90°,∴∠ABC=60°,∴∠OBC=30°,∴OC=12OB=12OA,即OA=2OC,故①正确;∵cos∠OBC=BCOB=32,∴BC=32OB,即BC=32OA,故②错误;∵∠ABO=∠OBC=30°,∴点O在∠ABC的平分线上,∴点O到直线AB的距离等于OC的长,∴以O为圆心,OC为半径的圆与AB相切,故③正确;如图,连接AD.∵AC⊥BD,∴DC=BC,∴AD=AB,又∵∠BAD=2∠BAC=60°,∴△ABD为等边三角形,∴AD=AB=BD,∴点A,B,D是☉O的三等分点,故④正确.结论正确的是①③④.
15.【解析】 (1)如图,△A1B1C1即为所求.
(2)点A'如图所示.
由图可知,a的取值范围是4
根据题意得48=x22+8,解得x=15,
即旗杆的高度为15m.
17.【解析】 (1)∵旋转四次恰好构成一个旋转对称图形,∴∠BCB'=360°÷5=72°.
(2)∵△A'B'C是由△ABC旋转得到的,
∴CB=CB',
∴△BCB'是等腰三角形.
18.【解析】 由三视图知该几何体是圆柱和长方体的组合体,
圆柱的底面直径为20mm,高为20mm,长方体的长、宽、高分别为30mm,25mm,40mm.
所以该几何体的表面积为(40×30+30×25+40×25)×2+π×(202)2+π×20×20-π×(202)2=5900+400π,
故该几何体的表面积是(5900+400π)mm2.
19.【解析】 (1)如图,连接OD.
∵AB=AC,OB=OD,∴∠B=∠C=∠ODB,∴OD∥AC,
∵DE⊥AC,∴∠CED=90°,∴∠ODE=90°,
又∵OD是☉O的半径,∴DE与☉O相切.
(2)如图,过点O作OF⊥BD于点F.
在Rt△OFB中,∠B=30°,OB=12AB=2,
∴OF=OB·sinB=1,BF=OB·cosB=3.
∴BD=2BF=23.
∵∠B=30°,∴∠AOD=60°.
阴影部分的面积为S△OBD+S扇形AOD=12×1×23+60π×22360=3+2π3.
20.【解析】 (1)AF是☉O的切线.理由如下:
连接OC,如图所示.
∵OF∥BC,∴∠1=∠2,∠B=∠3,
∵OC=OB,∴∠B=∠1,∴∠3=∠2,
在△OAF和△OCF中,OA=OC,∠3=∠2OF=OF,,∴△OAF≌△OCF(SAS),
∴∠OAF=∠OCF,
∵PC是☉O的切线,∴∠OCF=90°,
∴∠OAF=90°,∴FA⊥OA,
又∵OA是☉O的半径,∴AF是☉O的切线.
(2)∵AB是☉O的直径,∴∠BCA=90°,
∵OF∥BC,∴∠AEO=90°,即OF⊥AC.
∵☉O的半径为4,AF=3,∠OAF=90°,
∴OF=AF2+OA2=32+42=5,
∵FA⊥OA,OF⊥AC,∴AC=2AE,
△OAF的面积为12AF·OA=12OF·AE,
∴3×4=5×AE,解得AE=125,
∴AC=2AE=245.
21.【解析】 (1)如图,连接OC.
∵CD是☉O的切线,∴∠OCD=90°,
∵OA=OC,∴∠OAC=∠OCA,
∵PE⊥AB,∴∠PEA=90°,
∴∠OAC+∠APE=90°,∠OCA+∠PCD=90°,
∴∠APE=∠PCD,
∵∠APE=∠CPD,∴∠PCD=∠CPD,∴DC=DP.
(2)①43
如图,连接BC,
∵AB是直径,∴∠ACB=90°.
∵∠CAB=30°,AB=12,∴AC=AB·cos30°=63,
在Rt△APE中,∵AE=12OA=3,∴AP=AEcos30°=23,
∴PC=AC-AP=43,
∵∠APE=∠DPC=60°,DP=DC,∴△DPC是等边三角形,∴DC=43.
②3
当AE=EO=3时,四边形AOCF是菱形.理由如下:
如图,连接AF,OF.
∵AE=EO,FE⊥OA,∴FA=FO=OA,∴△AFO是等边三角形,∴∠FAO=60°,
∵∠CAB=30°,∴∠FAC=30°,∴∠FOC=2∠FAC=60°,
∴△FOC是等边三角形,∴CF=CO=OA=AF,∴四边形AOCF是菱形,
∴AE=3cm时,四边形AOCF是菱形.
22.【解析】 (1)不会发生变化的是△AOB的外接圆的半径.
理由如下:
∵∠AOB=90°,∴AB是△AOB的外接圆的直径,
∵AB=10,∴△AOB的外接圆的半径为5.
∴△AOB的外接圆的半径不变.
(2)如图,连接EK,KF.
则∠KEO=∠OFK=∠EOF=90°,
∴四边形EOFK是矩形.
又∵KE=KF,
∴四边形EOFK是正方形.
设☉K的半径为r,
则OE=OF=r,
∵AP=AE=4,AB=10,∴BF=PB=6.
∴在Rt△AOB中,有(4+r)2+(6+r)2=102,
解得r=2(负值已舍去),
故☉K的半径为2.
(3)在Rt△AOB中,OA2+OB2=AB2,
即(a+r)2+(10-a+r)2=102,
∴r2+10r=-a2+10a.
∴S=12r(OA+OB+AB)=12r(r+a+10-a+r+10)=r2+10r=-a2+10a=-(a-5)2+25,
∴当a=5时,S有最大值,此时AE=BF=5,
∴OA=OB=102=52.
23.【解析】 (1)正方形
(2)连接BD,AE.
∵∠BAC=90°,∴BD为四边形ABED的外接圆的直径,
∴∠BED=∠CED=90°.
∵四边形ABED为圆内接四边形,∴∠CDE=∠ABC,
∵∠ABC=∠C,∴∠EDC=∠C,
∴△DEC是等腰直角三角形.
∵四边形ABED为“圆美四边形”,∴BD⊥AE,∴AD=DE,
∴在等腰直角三角形CDE中,CD=2DE,∴CD=2AD,
∴AC=(2+1)AD,
∵AB=AC,AD=DE,∴ABDE=2+1.
(3)①∵PA⊥PD,PB⊥PE,∴∠APD=∠BPE=90°,
∵∠PBC=∠ADP,∴△APD∽△EPB,∴APPD=EPPB,
又∵∠APD+∠DPE=∠BPE+∠DPE,即∠APE=∠DPB,
∴△APE∽△DPB,∴∠AEP=∠DBP,
又∵∠DBP+∠PGB=90°,∠PGB=∠EGF,
∴∠AEP+∠EGF=90°,
∴∠BFE=90°,即BD⊥AE,
又∵A,B,E,D在同一个圆上,∴四边形ABED为“圆美四边形”.
②∵BD⊥AE,
∴AD2+BE2=AF2+FD2+BF2+EF2,AB2+DE2=AF2+BF2+DF2+EF2,
∴AD2+BE2=AB2+DE2,
∵A,B,E,D在同一个圆上,∴∠CDE=∠CBA,
∵∠C=∠C,∴△CDE∽△CBA,∴DEAB=CDBC=33,
设PA=x,DE=y,则PE=8-x,AB=3y,
∵α=30°,∠APD=∠BPE=90°,∴AD=2x,BE=2(8-x),
∴y2+(3y)2=(2x)2+[2(8-x)]2,
∴y2=x2+(8-x)2=2x2-16x+64=2(x-4)2+32,
∴当x=4时,y取到最小值42,即DE的最小值为42.
同课章节目录
