第27章 圆 单元测试卷(含解析)
图片预览




文档简介
华师大版九年级数学下册第27章 圆 单元测试卷
一、选择题(本大题共10个小题,每题3分,共30分)
1.下列说法正确的是 ( )
A.三点确定一个圆 B.一个三角形只有一个外接圆
C.和半径垂直的直线是圆的切线 D.三角形的内心到三角形三个顶点的距离相等
2.如图,等腰直角三角板ABC的斜边AB与量角器的直径重合,点D是量角器上60°刻度线的外端点,连接CD交AB于点E,则∠CEB的度数为 ( )
A.60° B.65° C.70° D.75°
第2题图 第3题图
3.如图,AB为☉O的直径,PD切☉O于点C,交AB的延长线于点D,且CO=CD,则∠PCA= ( )
A.30° B.45° C.60° D.67.5°
4.在平面直角坐标系中,点A的坐标为(1,0),点B的坐标为(a,0),☉A的半径为2,则下列说法中不正确的是( )
A.当a=-1时,点B在☉A上 B.当a<1时,点B在☉A内
C.当a<-1时,点B在☉A外 D.当-1 5.如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,4),(5,4),(1,-2),则△ABC外接圆圆心的坐标是 ( )
A.(2,3) B.(3,2) C.(1,3) D.(3,1)
第5题图 第6题图 第7题图 第8题图
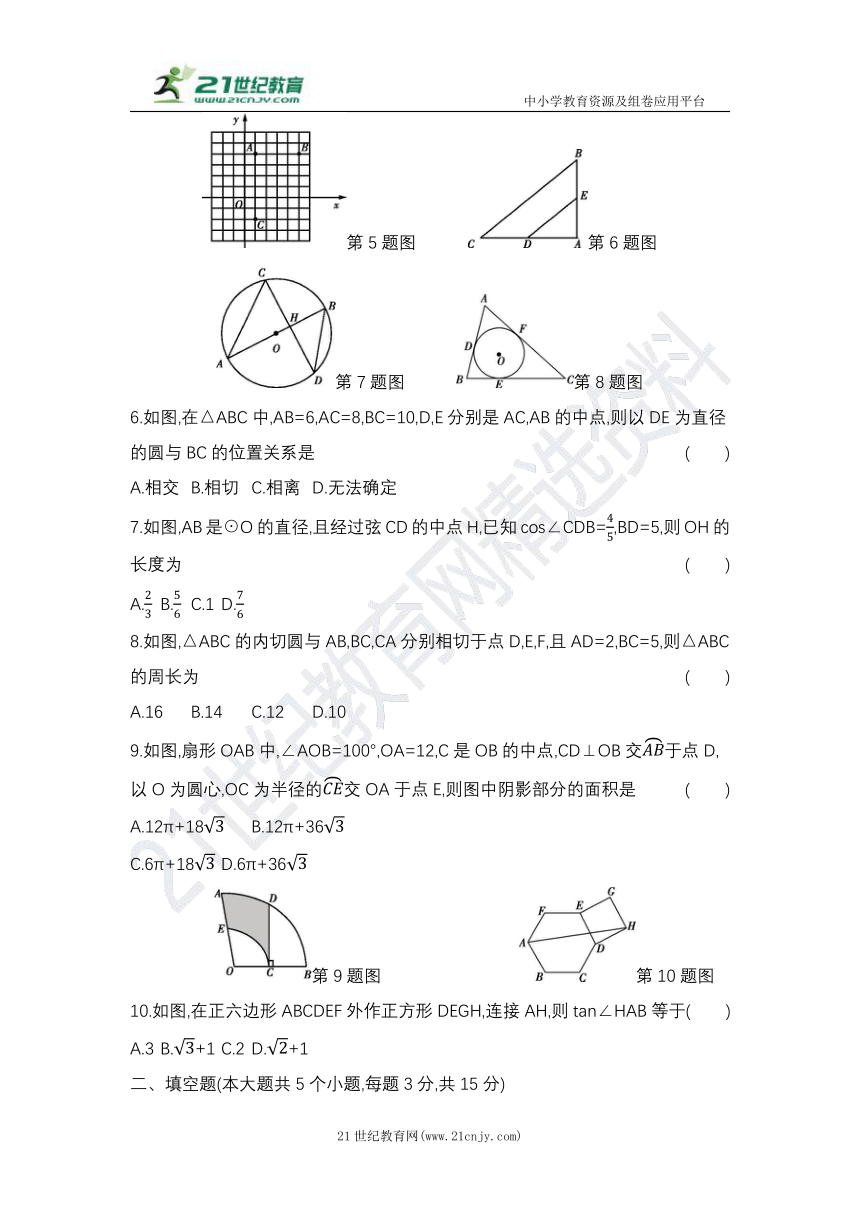
6.如图,在△ABC中,AB=6,AC=8,BC=10,D,E分别是AC,AB的中点,则以DE为直径的圆与BC的位置关系是 ( )
A.相交 B.相切 C.相离 D.无法确定
7.如图,AB是☉O的直径,且经过弦CD的中点H,已知cos∠CDB=45,BD=5,则OH的长度为 ( )
A.23 B.56 C.1 D.76
8.如图,△ABC的内切圆与AB,BC,CA分别相切于点D,E,F,且AD=2,BC=5,则△ABC的周长为 ( )
A.16 B.14 C.12 D.10
9.如图,扇形OAB中,∠AOB=100°,OA=12,C是OB的中点,CD⊥OB交AB于点D,以O为圆心,OC为半径的CE交OA于点E,则图中阴影部分的面积是 ( )
A.12π+183 B.12π+363
C.6π+183 D.6π+363
第9题图 第10题图
10.如图,在正六边形ABCDEF外作正方形DEGH,连接AH,则tan∠HAB等于 ( )
A.3 B.3+1 C.2 D.2+1
二、填空题(本大题共5个小题,每题3分,共15分)
11.线段AB=10cm,在以AB为直径的圆上,到点A的距离为5cm的点有 个.?
12.如图,AB,CD是☉O的直径,AE=BD.若∠AOE=32°,则∠COE的度数是 .?
第12题图 第14题图
13.☉O为△ABC的外接圆,∠BOC=100°,则∠A= .?
14.如图,AB是☉O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发在AB上沿着A→B方向运动(到点B停止运动),设运动时间为ts,连接EF,当△BEF是直角三角形时,t的值为 . ?
15.点A,C为半径是3的圆周上两点,点B为AC的中点,以线段BA,BC为邻边作菱形ABCD,顶点D恰在该圆直径的三等分点处,则该菱形的边长为 .?
三、解答题(本大题共8个小题,共75分)
16.(8分)如图,已知☉O的直径为10,点A,B,C在☉O上,∠CAB的平分线交☉O于点D.若∠CAB=60°,求BD的长.
17.(8分)如图,已知BC是☉O的直径,AC切☉O于点C,AB交☉O于点D,E为AC的中点,连接DE.
(1)若AD=DB,OC=5,求AC的长;
(2)求证:ED是☉O的切线.
18.(8分)如图,一个圆锥的高为33cm,侧面展开图是一个半圆.
求:(1)圆锥的母线长与底面半径的比;
(2)∠BAC的度数;
(3)圆锥的侧面积.(结果保留π)
19.(9分)如图,在△ABC中,以AC为直径的☉O分别交AB,BC于点D,E,连接DE,AD=BD,∠ADE=120°.
(1)试判断△ABC的形状并说明理由;
(2)若AC=2,求图中阴影部分的面积.
20.(9分)如图,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的切线,垂足为D,AB的延长线交直线CD于点E.
(1)求证:AC平分∠DAB;
(2)若AB=4,B为OE的中点,CF⊥AB,垂足为点F,求CF的长.
21.(10分)如图,☉O的半径为1,点A,P,B,C是☉O上的四个点,∠APC=∠CPB=60°.
(1)求证:△ABC是等边三角形;
(2)填空:
①PC,PB,PA之间的数量关系是 ;?
②四边形APBC面积的最大值为 .?
22.(11分)四边形ABCD的对角线交于点E,且AE=EC,BE=ED,以AB为直径的半圆过点E,圆心为O.
(1)如图1,求证:四边形ABCD是菱形;
(2)如图2,若CD的延长线与半圆相切于点F,且直径AB=8,连接OE,
①△OBE的面积为 ;?
②BE的长为 .?
23.(12分)问题情境:如图1,P是☉O外的一点,直线PO分别交☉O于点A,B,可以发现PA的长是点P到☉O上的点的最短距离.
(1)直接运用:如图2,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是CD上的一个动点,连接AP,则AP长度的最小值是 ;?
(2)综合运用:如图3,在平面直角坐标系中,分别以点A(-2,3),B(3,4)为圆心,分别以1,2为半径作☉A,☉B,M,N分别是☉A,☉B上的动点,P为x轴上的动点,则PM+PN的最小值等于 ;?
(3)构造运用:如图4,在边长为8的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A'MN,连接A'C,请求出A'C长度的最小值.
答案解析
1.B 【解析】 不共线的三点确定一个圆,所以选项A错误;一个三角形只有一个外接圆,所以选项B正确;过半径的外端与半径垂直的直线是圆的切线,所以选项C错误;三角形的内心到三角形三边的距离相等,所以选项D错误.故选B.
2.D 【解析】 ∵等腰直角三角板ABC的斜边AB与量角器的直径重合,∴点A,B,C,D都在以AB为直径的圆上,且∠B=45°.设AB的中点为O,∵点D对应60°,即∠AOD=60°,∴∠ACD=12∠AOD=30°,∴∠BCD=90°-∠ACD=60°,∴∠CEB=180°-∠BCD-∠B=180°-60°-45°=75°.故选D.
3.D 【解析】 因为PD是☉O的切线,所以∠OCD=∠OCP=90°.因为CO=CD,所以∠COD=45°.因为OA=OC,所以∠ACO=∠OAC=22.5°.所以∠PCA=90°-∠ACO=67.5°.故选D.
4.B 【解析】 如图,∵☉A的半径是2,∴AC=AE=2.∵点A的坐标为(1,0),∴OA=1,∴OE=1,OC=3.当a=-1时,点B在点E处,即点B在☉A上,正确,故A项不合题意;当a<1时,点B在☉A上或在☉A的内部或者在☉A的外部,如当a=-3时,点B在☉A的外部,错误,故B项符合题意;当a<-1时,AB>2,即点B在☉A的外部,正确,故C项不合题意;当-15.D
6.A 【解析】 如图,过点A作AM⊥BC于点M,交DE于点N.在△ABC中,AB=6,AC=8,BC=10,即AB2+AC2=BC2,∴△ABC是直角三角形,且∠CAB=90°,∴AM·BC=AC·AB,∴AM=6×810=4.8.∵D,E分别是AC,AB的中点,∴DE是△ABC的中位线,∴AN=MN=12AM=2.4,DE=12BC=5.∵以DE为直径的圆的半径为2.5,∴r=2.5>2.4,∴以DE为直径的圆与BC的位置关系是相交.故选A.
7.D 【解析】 连接OD.∵AB是☉O的直径,且经过弦CD的中点H,∴AB⊥CD,∴∠OHD=∠BHD=90°,∴cos∠CDB=DHBD=45,又∵BD=5,∴DH=4,∴BH=BD2-DH2=3.设OH=x,则OD=OB=x+3,在Rt△ODH中,由勾股定理得OH2+DH2=OD2,∴x2+42=(x+3)2,解得x=76,∴OH=76.故选D.
8.B 【解析】 ∵△ABC的内切圆与AB,BC,CA分别相切于点D,E,F,∴AF=AD=2,BD=BE,CE=CF.∵BE+CE=BC=5,∴BD+CF=BC=5,∴△ABC的周长为2+2+5+5=14.
9.C 【解析】 如图,连接OD,BD.∵C为OB的中点,∴OC=12OB=12OA=12OD.又∵CD⊥OB,∴∠CDO=30°,∠DOC=60°,OD=OA=12,OC=CB=6,∴CD=OD2-OC2=63,∴S阴影=S扇形AOB-S扇形COE-(S扇形BOD-S△COD)=100π×122360-100π×62360-(60π×122360-12×6×63)=183+6π.故选C.
10.B 【解析】 如图,连接BD,由正六边形和正方形的性质,得B,D,H三点共线,且∠ABH=90°.设正六边形ABCDEF的边长为a,则AB=BC=CD=DE=a.∵在△BCD中,BC=CD=a,∠BCD=120°,∴BD=3a,∴BH=DB+DH=(3+1)a.在Rt△ABH中,tan∠HAB=BHAB=3+1.
11.2 【解析】 如图,以A为圆心,5cm长为半径作圆,则该圆与以AB为直径的圆有2个交点,故在以AB为直径的圆上,到点A的距离为5cm的点有2个.
12.64° 【解析】 ∵AE=BD,∴∠BOD=∠AOE=32°.∵∠BOD=∠AOC,∴∠AOC=32°,∴∠COE=32°+32°=64°.
13.50°或130° 【解析】 分两种情况:当O在△ABC内部时,根据圆周角定理得∠A=12∠BOC=12×100°=50°;当O在△ABC外部时,∠A=180°-50°=130°.
14.1或74 【解析】 ∵AB是☉O的直径,∴∠ACB=90°.又∵∠ABC=60°,∴AB=2BC=4cm.∵F是弦BC的中点,∴BF=12BC=1cm.当∠BFE=90°时,∠B=60°,BE=2BF=2cm,则AE=AB-BE=2cm,此时t=1;当∠BEF=90°时,∠ABC=60°,BE=12BF=12cm,则AE=AB-BE=72cm,此时t=722=74.综上所述,t的值为1或74.
15.6或23 【解析】 设圆心为O,过B作直径,连接AC交BO于E,连接OC.∵点B为AC的中点,∴BD⊥AC.①如图1,∵点D在直径的三等分点处,∴BD=13×2×3=2,∴OD=OB-BD=1,∵四边形ABCD是菱形,∴DE=12BD=1,∴OE=2,∴CE=OC2-OE2=5,∴CD=DE2+CE2=6;如图2,BD=23×2×3=4,OD=BD-OB=1,DE=12BD=2,OE=DE-OD=1,∴CE=OC2-OE2=8=22,∴CD=CE2+DE2=(22)2+22=23.综上,该菱形的边长为6或23.
16.【解析】 如图,连接OB,OD.
∵∠CAB的平分线交☉O于点D,
∴∠BAD=12∠CAB=12×60°=30°,
∴∠BOD=2∠BAD=60°.
又∵OB=OD,
∴△OBD为等边三角形.
∵☉O的直径为10,∴BD=OB=5.
-508015938500
17.【解析】 (1)如图,连接OD,
∵AD=DB,OB=OC=5,
∴OD为△ABC的中位线,
∴AC=2OD=10.
(2)如图,连接CD,
∵AC切☉O于点C,∴AC⊥BC.
∵BC是☉O的直径,
∴∠BDC=90°,即BD⊥DC.
又∵E为AC的中点,
∴DE=EC=12AC,∴∠1=∠2.
∵OD=OC,∴∠3=∠4,
∴∠1+∠3=∠2+∠4=90°,∴DE⊥OD.
又∵点D在☉O上,
∴ED是☉O的切线.
18.【解析】 如图,设此圆锥的高AO为hcm,底面半径OC为rcm,母线AC长为lcm.
(1)∵2πr=180×πl180,∴lr=2.
故圆锥的母线长与底面半径的比为2.
(2)∵AO⊥BC,lr=2,∴圆锥的高AO与母线AC的夹角为30°,即∠OAC=30°.
又∵∠BAC=2∠OAC,∴∠BAC=60°.
(3)由图可知l2=h2+r2,∵h=33cm,
∴(2r)2=(33)2+r2,即4r2=27+r2,
∴r=3或r=-3(舍去),∴l=2r=6cm,
∴圆锥的侧面积为πl22=18πcm2
.
19.【解析】 (1)△ABC是等边三角形.
理由如下:
如图,连接CD,
∵AC为☉O的直径,∴CD⊥AB.
又∵AD=BD,∴AC=BC.
∵∠ADE=120°,∴∠ACE=60°,
∴△ABC是等边三角形.
(2)∵△ABC是等边三角形,∴∠A=∠ACB=∠B=60°,
∴∠BED=∠BDE=∠B=60°,
∴△BDE是等边三角形,∴BD=ED.
∵AD=BD,∴DE=AD,
∴DE=AD,∴S弓形DE=S弓形AD,∴S阴影=S△DEB.
∵AC=2,∴BD=1,
∴S阴影=S△DEB=34.
20.【解析】 (1)如图,连接OC.
∵直线CE与☉O相切于点C,∴OC⊥CE.
∵AD⊥CE,∴OC∥AD,
∴∠1=∠3.
∵OA=OC,∴∠2=∠3,
∴∠1=∠2,
∴AC平分∠DAB.
-1123951206500
(2)∵AB=4,B为OE的中点,
∴OC=2,OB=BE=2.
在Rt△OCE中,∵OC=12OE,
∴∠E=30°,∴∠COE=60°,∴∠OCF=30°.
在Rt△OCF中,∵∠OCF=30°,
∴OF=12OC=1,∴CF=3OF=3.
21.【解析】 (1)在☉O中,∠BAC与∠CPB是BC所对的圆周角,
∠ABC与∠APC是AC所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC.
∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形.
(2)①PC=PB+PA
如图1,在PC上截取PD=PA,
又∵∠APC=60°,∴△APD是等边三角形,
∴AD=AP=PD,∠ADP=60°,∴∠ADC=120°.
又∵∠APB=∠APC+∠BPC=120°,∴∠ADC=∠APB,
在△APB和△ADC中,∠ABP=∠ACD,∠APB=∠ADC,AP=AD,
∴△APB≌△ADC(A.A.S.),∴PB=CD.
又∵PD=AP,∴PC=PB+PA.
②3
当点P为AB的中点时,四边形APBC的面积最大.理由如下:
如图2,过点P作PE⊥AB,垂足为E,过点C作CF⊥AB,垂足为F.
∵S△APB=12AB·PE,S△ABC=12AB·CF,
∴S四边形APBC=12AB·(PE+CF),
当点P为AB的中点时,PE+CF=PC,PC为☉O的直径,
∴此时四边形APBC的面积最大.
∵☉O的半径为1,∴其内接正三角形的边长AB=3,
∴四边形APBC面积的最大值为12×2×3=3.
22.【解析】 (1)∵AE=EC,BE=ED,
∴四边形ABCD是平行四边形.
∵以AB为直径的半圆过点E,
∴∠AEB=90°,∴AC⊥BD.
又∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
(2)①4
如图,连接OF.
∵CD的延长线与半圆相切于点F,
∴OF⊥CF.
∵FC∥AB,∴OF等于△ABD中AB边上的高,
∴S△ABD=12×8×4=16.
∵点O是AB的中点,点E是BD的中点,
∴S△OBE=14S△ABD=4.
②23π
如图,过点D作DH⊥AB于点H.
∵AB∥CD,OF⊥CF,∴FO⊥AB,
∴∠F=∠FOB=∠DHO=90°,
∴四边形OHDF为矩形,∴DH=OF=4.
∵在Rt△DAH中,sin∠DAH=DHAD=12,
∴∠DAH=30°.
∵点O,E分别为AB,BD的中点,
∴OE∥AD,∴∠EOB=∠DAH=30°,
∴BE的长为30π×4180=23π.
23.【解析】 (1)5-1
如图1,取BC的中点E,连接AE,交半圆于P',连接EP,
在△AEP中,AP+EP>AE,
∴AP'的长是AP长度的最小值.
∵AE=AC2+CE2=5,P'E=1,
∴AP'=AE-P'E=5-1.
(2)74-3
如图2,作☉B关于x轴的对称圆☉B',连接AB'交x轴于P,此时PM+PN的值最小.
∵B(3,4),∴B'(3,-4).
∵A(-2,3),∴AB'=(3+2)2+(4+3)2=74.
∴PM+PN的最小值为AB'-AM-B'N'=AB'-AM-BN=74-3.
(3)如图3,由折叠知,A'M=AM,
∵M是AD的中点,
∴A'M=AM=MD,
∴点A'在以AD为直径的圆上,
∴当点A'在CM上时(即A″),A'C的长度取得最小值,
过点M作MH⊥CD交CD的延长线于H,
在Rt△MDH中,DH=DM·cos∠HDM=2,MH=DM·sin∠HDM=23,
在Rt△CHM中,CM=MH2+CH2=47,
∴A'C长度的最小值为CM-A″M=47-4.
一、选择题(本大题共10个小题,每题3分,共30分)
1.下列说法正确的是 ( )
A.三点确定一个圆 B.一个三角形只有一个外接圆
C.和半径垂直的直线是圆的切线 D.三角形的内心到三角形三个顶点的距离相等
2.如图,等腰直角三角板ABC的斜边AB与量角器的直径重合,点D是量角器上60°刻度线的外端点,连接CD交AB于点E,则∠CEB的度数为 ( )
A.60° B.65° C.70° D.75°
第2题图 第3题图
3.如图,AB为☉O的直径,PD切☉O于点C,交AB的延长线于点D,且CO=CD,则∠PCA= ( )
A.30° B.45° C.60° D.67.5°
4.在平面直角坐标系中,点A的坐标为(1,0),点B的坐标为(a,0),☉A的半径为2,则下列说法中不正确的是( )
A.当a=-1时,点B在☉A上 B.当a<1时,点B在☉A内
C.当a<-1时,点B在☉A外 D.当-1
A.(2,3) B.(3,2) C.(1,3) D.(3,1)
第5题图 第6题图 第7题图 第8题图
6.如图,在△ABC中,AB=6,AC=8,BC=10,D,E分别是AC,AB的中点,则以DE为直径的圆与BC的位置关系是 ( )
A.相交 B.相切 C.相离 D.无法确定
7.如图,AB是☉O的直径,且经过弦CD的中点H,已知cos∠CDB=45,BD=5,则OH的长度为 ( )
A.23 B.56 C.1 D.76
8.如图,△ABC的内切圆与AB,BC,CA分别相切于点D,E,F,且AD=2,BC=5,则△ABC的周长为 ( )
A.16 B.14 C.12 D.10
9.如图,扇形OAB中,∠AOB=100°,OA=12,C是OB的中点,CD⊥OB交AB于点D,以O为圆心,OC为半径的CE交OA于点E,则图中阴影部分的面积是 ( )
A.12π+183 B.12π+363
C.6π+183 D.6π+363
第9题图 第10题图
10.如图,在正六边形ABCDEF外作正方形DEGH,连接AH,则tan∠HAB等于 ( )
A.3 B.3+1 C.2 D.2+1
二、填空题(本大题共5个小题,每题3分,共15分)
11.线段AB=10cm,在以AB为直径的圆上,到点A的距离为5cm的点有 个.?
12.如图,AB,CD是☉O的直径,AE=BD.若∠AOE=32°,则∠COE的度数是 .?
第12题图 第14题图
13.☉O为△ABC的外接圆,∠BOC=100°,则∠A= .?
14.如图,AB是☉O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发在AB上沿着A→B方向运动(到点B停止运动),设运动时间为ts,连接EF,当△BEF是直角三角形时,t的值为 . ?
15.点A,C为半径是3的圆周上两点,点B为AC的中点,以线段BA,BC为邻边作菱形ABCD,顶点D恰在该圆直径的三等分点处,则该菱形的边长为 .?
三、解答题(本大题共8个小题,共75分)
16.(8分)如图,已知☉O的直径为10,点A,B,C在☉O上,∠CAB的平分线交☉O于点D.若∠CAB=60°,求BD的长.
17.(8分)如图,已知BC是☉O的直径,AC切☉O于点C,AB交☉O于点D,E为AC的中点,连接DE.
(1)若AD=DB,OC=5,求AC的长;
(2)求证:ED是☉O的切线.
18.(8分)如图,一个圆锥的高为33cm,侧面展开图是一个半圆.
求:(1)圆锥的母线长与底面半径的比;
(2)∠BAC的度数;
(3)圆锥的侧面积.(结果保留π)
19.(9分)如图,在△ABC中,以AC为直径的☉O分别交AB,BC于点D,E,连接DE,AD=BD,∠ADE=120°.
(1)试判断△ABC的形状并说明理由;
(2)若AC=2,求图中阴影部分的面积.
20.(9分)如图,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的切线,垂足为D,AB的延长线交直线CD于点E.
(1)求证:AC平分∠DAB;
(2)若AB=4,B为OE的中点,CF⊥AB,垂足为点F,求CF的长.
21.(10分)如图,☉O的半径为1,点A,P,B,C是☉O上的四个点,∠APC=∠CPB=60°.
(1)求证:△ABC是等边三角形;
(2)填空:
①PC,PB,PA之间的数量关系是 ;?
②四边形APBC面积的最大值为 .?
22.(11分)四边形ABCD的对角线交于点E,且AE=EC,BE=ED,以AB为直径的半圆过点E,圆心为O.
(1)如图1,求证:四边形ABCD是菱形;
(2)如图2,若CD的延长线与半圆相切于点F,且直径AB=8,连接OE,
①△OBE的面积为 ;?
②BE的长为 .?
23.(12分)问题情境:如图1,P是☉O外的一点,直线PO分别交☉O于点A,B,可以发现PA的长是点P到☉O上的点的最短距离.
(1)直接运用:如图2,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是CD上的一个动点,连接AP,则AP长度的最小值是 ;?
(2)综合运用:如图3,在平面直角坐标系中,分别以点A(-2,3),B(3,4)为圆心,分别以1,2为半径作☉A,☉B,M,N分别是☉A,☉B上的动点,P为x轴上的动点,则PM+PN的最小值等于 ;?
(3)构造运用:如图4,在边长为8的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A'MN,连接A'C,请求出A'C长度的最小值.
答案解析
1.B 【解析】 不共线的三点确定一个圆,所以选项A错误;一个三角形只有一个外接圆,所以选项B正确;过半径的外端与半径垂直的直线是圆的切线,所以选项C错误;三角形的内心到三角形三边的距离相等,所以选项D错误.故选B.
2.D 【解析】 ∵等腰直角三角板ABC的斜边AB与量角器的直径重合,∴点A,B,C,D都在以AB为直径的圆上,且∠B=45°.设AB的中点为O,∵点D对应60°,即∠AOD=60°,∴∠ACD=12∠AOD=30°,∴∠BCD=90°-∠ACD=60°,∴∠CEB=180°-∠BCD-∠B=180°-60°-45°=75°.故选D.
3.D 【解析】 因为PD是☉O的切线,所以∠OCD=∠OCP=90°.因为CO=CD,所以∠COD=45°.因为OA=OC,所以∠ACO=∠OAC=22.5°.所以∠PCA=90°-∠ACO=67.5°.故选D.
4.B 【解析】 如图,∵☉A的半径是2,∴AC=AE=2.∵点A的坐标为(1,0),∴OA=1,∴OE=1,OC=3.当a=-1时,点B在点E处,即点B在☉A上,正确,故A项不合题意;当a<1时,点B在☉A上或在☉A的内部或者在☉A的外部,如当a=-3时,点B在☉A的外部,错误,故B项符合题意;当a<-1时,AB>2,即点B在☉A的外部,正确,故C项不合题意;当-1
6.A 【解析】 如图,过点A作AM⊥BC于点M,交DE于点N.在△ABC中,AB=6,AC=8,BC=10,即AB2+AC2=BC2,∴△ABC是直角三角形,且∠CAB=90°,∴AM·BC=AC·AB,∴AM=6×810=4.8.∵D,E分别是AC,AB的中点,∴DE是△ABC的中位线,∴AN=MN=12AM=2.4,DE=12BC=5.∵以DE为直径的圆的半径为2.5,∴r=2.5>2.4,∴以DE为直径的圆与BC的位置关系是相交.故选A.
7.D 【解析】 连接OD.∵AB是☉O的直径,且经过弦CD的中点H,∴AB⊥CD,∴∠OHD=∠BHD=90°,∴cos∠CDB=DHBD=45,又∵BD=5,∴DH=4,∴BH=BD2-DH2=3.设OH=x,则OD=OB=x+3,在Rt△ODH中,由勾股定理得OH2+DH2=OD2,∴x2+42=(x+3)2,解得x=76,∴OH=76.故选D.
8.B 【解析】 ∵△ABC的内切圆与AB,BC,CA分别相切于点D,E,F,∴AF=AD=2,BD=BE,CE=CF.∵BE+CE=BC=5,∴BD+CF=BC=5,∴△ABC的周长为2+2+5+5=14.
9.C 【解析】 如图,连接OD,BD.∵C为OB的中点,∴OC=12OB=12OA=12OD.又∵CD⊥OB,∴∠CDO=30°,∠DOC=60°,OD=OA=12,OC=CB=6,∴CD=OD2-OC2=63,∴S阴影=S扇形AOB-S扇形COE-(S扇形BOD-S△COD)=100π×122360-100π×62360-(60π×122360-12×6×63)=183+6π.故选C.
10.B 【解析】 如图,连接BD,由正六边形和正方形的性质,得B,D,H三点共线,且∠ABH=90°.设正六边形ABCDEF的边长为a,则AB=BC=CD=DE=a.∵在△BCD中,BC=CD=a,∠BCD=120°,∴BD=3a,∴BH=DB+DH=(3+1)a.在Rt△ABH中,tan∠HAB=BHAB=3+1.
11.2 【解析】 如图,以A为圆心,5cm长为半径作圆,则该圆与以AB为直径的圆有2个交点,故在以AB为直径的圆上,到点A的距离为5cm的点有2个.
12.64° 【解析】 ∵AE=BD,∴∠BOD=∠AOE=32°.∵∠BOD=∠AOC,∴∠AOC=32°,∴∠COE=32°+32°=64°.
13.50°或130° 【解析】 分两种情况:当O在△ABC内部时,根据圆周角定理得∠A=12∠BOC=12×100°=50°;当O在△ABC外部时,∠A=180°-50°=130°.
14.1或74 【解析】 ∵AB是☉O的直径,∴∠ACB=90°.又∵∠ABC=60°,∴AB=2BC=4cm.∵F是弦BC的中点,∴BF=12BC=1cm.当∠BFE=90°时,∠B=60°,BE=2BF=2cm,则AE=AB-BE=2cm,此时t=1;当∠BEF=90°时,∠ABC=60°,BE=12BF=12cm,则AE=AB-BE=72cm,此时t=722=74.综上所述,t的值为1或74.
15.6或23 【解析】 设圆心为O,过B作直径,连接AC交BO于E,连接OC.∵点B为AC的中点,∴BD⊥AC.①如图1,∵点D在直径的三等分点处,∴BD=13×2×3=2,∴OD=OB-BD=1,∵四边形ABCD是菱形,∴DE=12BD=1,∴OE=2,∴CE=OC2-OE2=5,∴CD=DE2+CE2=6;如图2,BD=23×2×3=4,OD=BD-OB=1,DE=12BD=2,OE=DE-OD=1,∴CE=OC2-OE2=8=22,∴CD=CE2+DE2=(22)2+22=23.综上,该菱形的边长为6或23.
16.【解析】 如图,连接OB,OD.
∵∠CAB的平分线交☉O于点D,
∴∠BAD=12∠CAB=12×60°=30°,
∴∠BOD=2∠BAD=60°.
又∵OB=OD,
∴△OBD为等边三角形.
∵☉O的直径为10,∴BD=OB=5.
-508015938500
17.【解析】 (1)如图,连接OD,
∵AD=DB,OB=OC=5,
∴OD为△ABC的中位线,
∴AC=2OD=10.
(2)如图,连接CD,
∵AC切☉O于点C,∴AC⊥BC.
∵BC是☉O的直径,
∴∠BDC=90°,即BD⊥DC.
又∵E为AC的中点,
∴DE=EC=12AC,∴∠1=∠2.
∵OD=OC,∴∠3=∠4,
∴∠1+∠3=∠2+∠4=90°,∴DE⊥OD.
又∵点D在☉O上,
∴ED是☉O的切线.
18.【解析】 如图,设此圆锥的高AO为hcm,底面半径OC为rcm,母线AC长为lcm.
(1)∵2πr=180×πl180,∴lr=2.
故圆锥的母线长与底面半径的比为2.
(2)∵AO⊥BC,lr=2,∴圆锥的高AO与母线AC的夹角为30°,即∠OAC=30°.
又∵∠BAC=2∠OAC,∴∠BAC=60°.
(3)由图可知l2=h2+r2,∵h=33cm,
∴(2r)2=(33)2+r2,即4r2=27+r2,
∴r=3或r=-3(舍去),∴l=2r=6cm,
∴圆锥的侧面积为πl22=18πcm2
.
19.【解析】 (1)△ABC是等边三角形.
理由如下:
如图,连接CD,
∵AC为☉O的直径,∴CD⊥AB.
又∵AD=BD,∴AC=BC.
∵∠ADE=120°,∴∠ACE=60°,
∴△ABC是等边三角形.
(2)∵△ABC是等边三角形,∴∠A=∠ACB=∠B=60°,
∴∠BED=∠BDE=∠B=60°,
∴△BDE是等边三角形,∴BD=ED.
∵AD=BD,∴DE=AD,
∴DE=AD,∴S弓形DE=S弓形AD,∴S阴影=S△DEB.
∵AC=2,∴BD=1,
∴S阴影=S△DEB=34.
20.【解析】 (1)如图,连接OC.
∵直线CE与☉O相切于点C,∴OC⊥CE.
∵AD⊥CE,∴OC∥AD,
∴∠1=∠3.
∵OA=OC,∴∠2=∠3,
∴∠1=∠2,
∴AC平分∠DAB.
-1123951206500
(2)∵AB=4,B为OE的中点,
∴OC=2,OB=BE=2.
在Rt△OCE中,∵OC=12OE,
∴∠E=30°,∴∠COE=60°,∴∠OCF=30°.
在Rt△OCF中,∵∠OCF=30°,
∴OF=12OC=1,∴CF=3OF=3.
21.【解析】 (1)在☉O中,∠BAC与∠CPB是BC所对的圆周角,
∠ABC与∠APC是AC所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC.
∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形.
(2)①PC=PB+PA
如图1,在PC上截取PD=PA,
又∵∠APC=60°,∴△APD是等边三角形,
∴AD=AP=PD,∠ADP=60°,∴∠ADC=120°.
又∵∠APB=∠APC+∠BPC=120°,∴∠ADC=∠APB,
在△APB和△ADC中,∠ABP=∠ACD,∠APB=∠ADC,AP=AD,
∴△APB≌△ADC(A.A.S.),∴PB=CD.
又∵PD=AP,∴PC=PB+PA.
②3
当点P为AB的中点时,四边形APBC的面积最大.理由如下:
如图2,过点P作PE⊥AB,垂足为E,过点C作CF⊥AB,垂足为F.
∵S△APB=12AB·PE,S△ABC=12AB·CF,
∴S四边形APBC=12AB·(PE+CF),
当点P为AB的中点时,PE+CF=PC,PC为☉O的直径,
∴此时四边形APBC的面积最大.
∵☉O的半径为1,∴其内接正三角形的边长AB=3,
∴四边形APBC面积的最大值为12×2×3=3.
22.【解析】 (1)∵AE=EC,BE=ED,
∴四边形ABCD是平行四边形.
∵以AB为直径的半圆过点E,
∴∠AEB=90°,∴AC⊥BD.
又∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
(2)①4
如图,连接OF.
∵CD的延长线与半圆相切于点F,
∴OF⊥CF.
∵FC∥AB,∴OF等于△ABD中AB边上的高,
∴S△ABD=12×8×4=16.
∵点O是AB的中点,点E是BD的中点,
∴S△OBE=14S△ABD=4.
②23π
如图,过点D作DH⊥AB于点H.
∵AB∥CD,OF⊥CF,∴FO⊥AB,
∴∠F=∠FOB=∠DHO=90°,
∴四边形OHDF为矩形,∴DH=OF=4.
∵在Rt△DAH中,sin∠DAH=DHAD=12,
∴∠DAH=30°.
∵点O,E分别为AB,BD的中点,
∴OE∥AD,∴∠EOB=∠DAH=30°,
∴BE的长为30π×4180=23π.
23.【解析】 (1)5-1
如图1,取BC的中点E,连接AE,交半圆于P',连接EP,
在△AEP中,AP+EP>AE,
∴AP'的长是AP长度的最小值.
∵AE=AC2+CE2=5,P'E=1,
∴AP'=AE-P'E=5-1.
(2)74-3
如图2,作☉B关于x轴的对称圆☉B',连接AB'交x轴于P,此时PM+PN的值最小.
∵B(3,4),∴B'(3,-4).
∵A(-2,3),∴AB'=(3+2)2+(4+3)2=74.
∴PM+PN的最小值为AB'-AM-B'N'=AB'-AM-BN=74-3.
(3)如图3,由折叠知,A'M=AM,
∵M是AD的中点,
∴A'M=AM=MD,
∴点A'在以AD为直径的圆上,
∴当点A'在CM上时(即A″),A'C的长度取得最小值,
过点M作MH⊥CD交CD的延长线于H,
在Rt△MDH中,DH=DM·cos∠HDM=2,MH=DM·sin∠HDM=23,
在Rt△CHM中,CM=MH2+CH2=47,
∴A'C长度的最小值为CM-A″M=47-4.
