2019-2020学年湖南省株洲市攸县震林中学八年级下学期期中数学试卷 (word版,含解析)
文档属性
| 名称 | 2019-2020学年湖南省株洲市攸县震林中学八年级下学期期中数学试卷 (word版,含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 914.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-03 06:32:36 | ||
图片预览




文档简介
2019-2020学年湖南省株洲市攸县震林中学八年级第二学期期中数学试卷
一、选择题
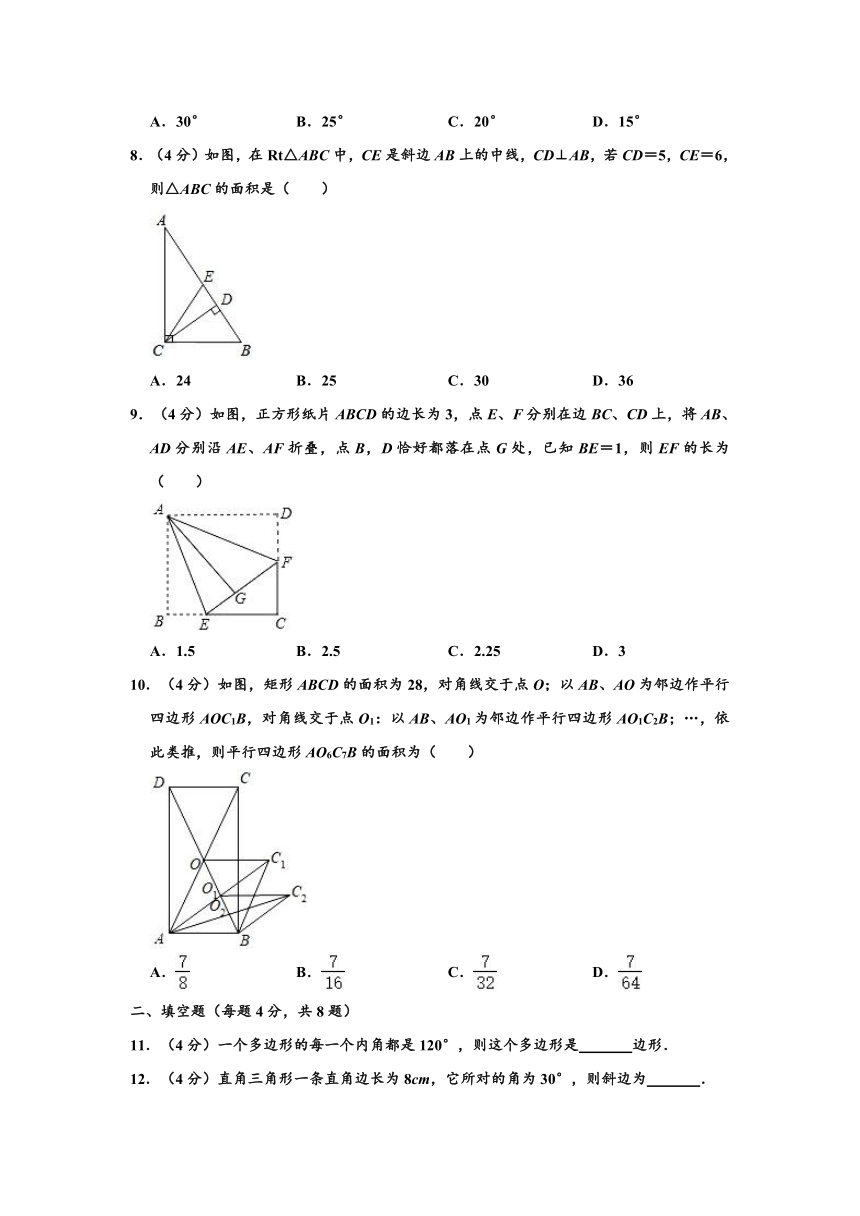
1.(4分)下列图形是中心对称图形的是( )
A. B.
C. D.
2.(4分)下列各组线段能构成直角三角形的一组是( )
A.9,40,41 B.7,12,13 C.5,9,12 D.3,4,6
3.(4分)已知过一个多边形的一个顶点可以引2条对角线,则它是( )
A.六边形 B.五边形 C.四边形 D.三角形
4.(4分)关于?ABCD的叙述,正确的是( )
A.若AC=BD,则?ABCD是菱形
B.若AB=AD,则?ABCD是矩形
C.若AB⊥BC,则?ABCD是正方形
D.若AC⊥BD,则?ABCD是菱形
5.(4分)菱形的两条对角线分别是12和16,则此菱形的边长是( )
A.10 B.8 C.6 D.5
6.(4分)如图,在△ABC中,AC=10,DE是△ABC的中位线,则DE的长度是( )
A.3 B.4 C.4.8 D.5
7.(4分)如图,菱形ABCD中,∠B=120°,则∠1的度数是( )
A.30° B.25° C.20° D.15°
8.(4分)如图,在Rt△ABC中,CE是斜边AB上的中线,CD⊥AB,若CD=5,CE=6,则△ABC的面积是( )
A.24 B.25 C.30 D.36
9.(4分)如图,正方形纸片ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别沿AE、AF折叠,点B,D恰好都落在点G处,已知BE=1,则EF的长为( )
A.1.5 B.2.5 C.2.25 D.3
10.(4分)如图,矩形ABCD的面积为28,对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1:以AB、AO1为邻边作平行四边形AO1C2B;…,依此类推,则平行四边形AO6C7B的面积为( )
A. B. C. D.
二、填空题(每题4分,共8题)
11.(4分)一个多边形的每一个内角都是120°,则这个多边形是 边形.
12.(4分)直角三角形一条直角边长为8cm,它所对的角为30°,则斜边为 .
13.(4分)如图,在△ABC中,∠C=90°,AD是角平分线,CD=9,则点D到AB的距离为 .
14.(4分)如图,直线l上有三个正方形,A,B,C,若A,C的面积分别为36和64,则B的面积为 .
15.(4分)如图,?ABCD的周长是22,△ABC的周长是17,则AC的长为 .
16.(4分)如图,在平行四边形ABCD中,AB=,AD=4,AC⊥BC.则BD= .
17.(4分)已知四边形ABCD是正方形,以AD为边在正方形ABCD所在平面内作等边三角形PAD,那么∠BPC的度数是 .
18.(4分)如图,在梯形ABCD中,AD∥BC,AD=4,BC=12,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间为 秒时,以点P,Q,E,D为顶点的四边形是平行四边形.
三、解答题(共8题,共78分)
19.(8分)如图,在四边形ABCD中,∠C+∠D=210°
(1)∠DAB+∠CBA= 度;
(2)若∠DAB的角平分线与∠CBA的角平分线相交于点E,求∠E的度数.
20.(8分)如图,已知∠AOB=30°,P是∠AOB平分线上一点,CP∥OB,交OA于点C,PD⊥OB,垂足为点D,且PC=6,求PD的长.(提示:过点P作PE⊥OA于点E)
21.(8分)如图所示的一块地(图中阴影部分)∠ADC=90°,AD=4,CD=3,AB=13,BC=12
(1)求∠ACB的度数;
(2)求阴影部分的面积.
22.(8分)已知:如图,在矩形ABCD中,点E在边AB上,点F在边BC上,且BE=CF,EF⊥DF,求证:BF=CD.
23.(10分)如图,已知A、B两艘船同时从港口O出发,船A以40km/h的速度向东航行;船B以30km/h的速度向北航行,它们离开港口2h后相距多远?
24.(10分)已知,如图,在Rt△ABC中,E是两锐角平分线的交点,ED⊥BC,EF⊥AC,垂足分别为D,F,求证:四边形CDEF是正方形.
25.(12分)如图,在Rt△ABC中,∠B=90°,AC=40cm,∠A=60°,点D从点C出发沿CA方向以2cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以1cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是a秒(0<a≤20).过点D作DF⊥BC于点F,连接DE,EF.
(1)四边形AEFD能够成为菱形吗?如果能,求出相应的a值;如果不能,请说明理由;
(2)当a为何值时,△DEF为直角三角形?请说明理由.
26.(14分)如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作平行四边形ECFG,如图1所示.
(1)证明平行四边形ECFG是菱形;
(2)若∠ABC=120°,连结BG、CG、DG,如图2所示,
①求证:△DGC≌△BGE;
②求∠BDG的度数;
(3)若∠ABC=90°,AB=8,AD=14,M是EF的中点,如图3所示,求DM的长.
参考答案
一.选择题(每小题4分,共10题)
1.(4分)下列图形是中心对称图形的是( )
A. B.
C. D.
解:A、C、D中图形都不是中心对称图形,
B中图形是中心对称图形,
故选:B.
2.(4分)下列各组线段能构成直角三角形的一组是( )
A.9,40,41 B.7,12,13 C.5,9,12 D.3,4,6
解:A、92+402=412,能构成直角三角形;
B、72+122≠132,不能构成直角三角形;
C、52+92≠122,不能构成直角三角形;
D、32+42≠62,不能构成直角三角形.
故选:A.
3.(4分)已知过一个多边形的一个顶点可以引2条对角线,则它是( )
A.六边形 B.五边形 C.四边形 D.三角形
解:设多边形的边数为n.
根据题意得;n﹣3=2.
解得:n=5.
故选:B.
4.(4分)关于?ABCD的叙述,正确的是( )
A.若AC=BD,则?ABCD是菱形
B.若AB=AD,则?ABCD是矩形
C.若AB⊥BC,则?ABCD是正方形
D.若AC⊥BD,则?ABCD是菱形
解:∵?ABCD中,AC=BD,
∴四边形ABCD是矩形,选项A不符合题意;
∵?ABCD中,AB=AD,
∴四边形ABCD是菱形,不一定是正方形,选项B不符合题意;
∵?ABCD中,AB⊥BC,
∴四边形ABCD是矩形,不一定是正方形,选项C不符合题意;
∵?ABCD中,AC⊥BD,
∴四边形ABCD是菱形,选项D符合题意;
故选:D.
5.(4分)菱形的两条对角线分别是12和16,则此菱形的边长是( )
A.10 B.8 C.6 D.5
解:如图,
∵菱形ABCD中,AC=12,BD=16,
∴OA=AC=6,OB=BD=8,AC⊥BD,
∴AB==10.
即菱形的边长是10.
故选:A.
6.(4分)如图,在△ABC中,AC=10,DE是△ABC的中位线,则DE的长度是( )
A.3 B.4 C.4.8 D.5
解:∵DE是△ABC的中位线,
∴DE=AC=×10=5,
故选:D.
7.(4分)如图,菱形ABCD中,∠B=120°,则∠1的度数是( )
A.30° B.25° C.20° D.15°
解:∵四边形ABCD是菱形,
∴AB=BC,
∵∠B=120°,
∴∠1==30°,
故选:A.
8.(4分)如图,在Rt△ABC中,CE是斜边AB上的中线,CD⊥AB,若CD=5,CE=6,则△ABC的面积是( )
A.24 B.25 C.30 D.36
解:∵CE是斜边AB上的中线,
∴AB=2CE=2×6=12,
∴S△ABC=×CD×AB=×5×12=30,
故选:C.
9.(4分)如图,正方形纸片ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别沿AE、AF折叠,点B,D恰好都落在点G处,已知BE=1,则EF的长为( )
A.1.5 B.2.5 C.2.25 D.3
解:∵正方形纸片ABCD的边长为3,
∴∠C=90°,BC=CD=3,
根据折叠的性质得:EG=BE=1,GF=DF,
设DF=x,
则EF=EG+GF=1+x,FC=DC﹣DF=3﹣x,EC=BC﹣BE=3﹣1=2,
∵在Rt△EFC中,EF2=EC2+FC2,即(x+1)2=22+(3﹣x)2,解得:x=1.5,
∴DF=1.5,EF=1+1.5=2.5.
故选:B.
10.(4分)如图,矩形ABCD的面积为28,对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1:以AB、AO1为邻边作平行四边形AO1C2B;…,依此类推,则平行四边形AO6C7B的面积为( )
A. B. C. D.
解:设矩形ABCD的面积为S,
根据题意得:平行四边形AOC1B的面积=矩形ABCD的面积=S,
平行四边形AO1C2B的面积=平行四边形AOC1B的面积=S=,…,
平行四边形AOn﹣1?nB的面积=,
∴平行四边形AOnCn+1B的面积=,
∴平行四边形AO6C7B的面积为==;
故选:C.
二、填空题(每题4分,共8题)
11.(4分)一个多边形的每一个内角都是120°,则这个多边形是 六 边形.
解:180﹣120=60,
多边形的边数是:360÷60=6.
则这个多边形是六边形.
12.(4分)直角三角形一条直角边长为8cm,它所对的角为30°,则斜边为 16cm .
解:如图,在Rt△ABC中,∠B=90°,∠A=30°,BC=8cm,则BC=AC=8cm,
所以AC=2BC=16cm.
故答案是:16cm.
13.(4分)如图,在△ABC中,∠C=90°,AD是角平分线,CD=9,则点D到AB的距离为 9 .
解:如图,过D作DE⊥AB于E,
∵AD是∠BAC的平分线,∠C=90°,
∴DE=DC=9,
即点D到AB的距离为9.
故答案为:9.
14.(4分)如图,直线l上有三个正方形,A,B,C,若A,C的面积分别为36和64,则B的面积为 100 .
解:如图,
∵图形A、B、C都是为正方形,
∴EF2=36,MN2=64,GE=GM,∠EGM=90°,
∴∠EGF+∠NGM=90°,
而∠EGF+∠FEG=90°,
∴∠FEG=∠NGM,
在△EFG和△GNM中,
,
∴△EFG≌△GNM,
∴GF=MN,
在Rt△EFG中,EG2=EF2+FG2=EG2+MN2=36+64=100,
∴正方形B的面积为100.
故答案为100.
15.(4分)如图,?ABCD的周长是22,△ABC的周长是17,则AC的长为 6 .
解:∵,?ABCD的周长是22,
∴AB+BC=11,
∵△ABC的周长是17,
∴AC=17﹣11=6,
故答案为:6
16.(4分)如图,在平行四边形ABCD中,AB=,AD=4,AC⊥BC.则BD= 10 .
解:∵四边形ABCD是平行四边形,
∴BC=AD=4,OB=OD,OA=OC,
∵AC⊥BC,
∴由勾股定理得:AC===6,
∴OC=AC=3,
∵在Rt△BCO中,∠BCO=90°,
∴OB===5,
∴BD=2OB=10,
故答案为:10.
17.(4分)已知四边形ABCD是正方形,以AD为边在正方形ABCD所在平面内作等边三角形PAD,那么∠BPC的度数是 30°或150° .
解:如图(1),
∵四边形ABCD是正方形,△PAD是等边三角形,
∴∠BAP=∠BAD+∠PAB=90°+60°=150°.
∵PA=AD,AB=AD,
∴PA=AB,
∴∠ABP=(180°﹣150°)=15°,
∴∠PBC=∠ABC﹣∠ABP=90°﹣15°=75°,
同理:∠PCB=75°,
∴∠BPC=180°﹣75°﹣75°=30°.
如图(2),∵四边形ABCD是正方形,△PAD是等边三角形,
∴∠BAP=∠BAD﹣∠PAB=90°﹣60°=30°.
∵PA=AD,AB=AD,
∴PA=AB,
∴∠APB=(180°﹣30°)=75°,
同理:∠CPD=75°,
∴∠BPC=360°﹣75°﹣75°﹣60°=150°.
综上可得:∠BPC的度数是30°或150°.
故答案为:30°或150°.
18.(4分)如图,在梯形ABCD中,AD∥BC,AD=4,BC=12,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间为 2或 秒时,以点P,Q,E,D为顶点的四边形是平行四边形.
解:∵E是BC的中点,
∴BE=CE=BC=×12=6,
①当Q运动到E和C之间,设运动时间为t,则AP=t,DP=AD﹣AP=4﹣t,CQ=2t,EQ=CE﹣CQ=6﹣2t,
∴4﹣t=6﹣2t,
解得:t=2;
②当Q运动到E和B之间,设运动时间为t,则AP=t,DP=AD﹣AP=4﹣t,CQ=2t,EQ=CQ﹣CE=2t﹣6,
∴4﹣t=2t﹣6,
解得:t=,
∴当运动时间t为2或秒时,以点P,Q,E,D为顶点的四边形是平行四边形.
故答案为:2或.
三、解答题(共8题,共78分)
19.(8分)如图,在四边形ABCD中,∠C+∠D=210°
(1)∠DAB+∠CBA= 150 度;
(2)若∠DAB的角平分线与∠CBA的角平分线相交于点E,求∠E的度数.
解:(1)∵∠DAB+∠CBA+∠C+∠D=360°,
∴∠DAB+∠CBA=360°﹣(∠C+∠D)=360°﹣210°=150°.
故答案为:150;
(2)∵∠DAB与∠ABC的平分线交于四边形内一点E,
∴∠EAB=∠DAB,∠EBA=∠ABC,
∴∠E=180°﹣(∠EAB+∠EBA)
=180°﹣(∠DAB+∠CBA)
=180°﹣(360°﹣∠C﹣∠D)
=(∠C+∠D),
∵∠C+∠D=210°,
∴∠E=(∠C+∠D)=105°.
20.(8分)如图,已知∠AOB=30°,P是∠AOB平分线上一点,CP∥OB,交OA于点C,PD⊥OB,垂足为点D,且PC=6,求PD的长.(提示:过点P作PE⊥OA于点E)
解:过点P作PE⊥OA于点E,如图所示,
∵OP平分∠AOB,PD⊥OB,PE⊥OA,∠AOB=30°,
∴∠COP=∠POD=15°,PD=PE,
∵CP∥OB,
∴∠POD=∠CPO,
∴∠COP+∠CPO=∠COP+∠POD=30°,
∴∠ECP=∠COP+∠CPO=30°,
∵PC=6,∠PEC=90°,
∴PE=3,
∴PD=3.
21.(8分)如图所示的一块地(图中阴影部分)∠ADC=90°,AD=4,CD=3,AB=13,BC=12
(1)求∠ACB的度数;
(2)求阴影部分的面积.
解:(1)在Rt△ADC中,由勾股定理得:AC===5,
∵AB=13,BC=12,AC=5,
∴AC2+BC2=AB2,
∴∠ACB=90°;
(2)阴影部分的面积S=S△ACB﹣S△ADC=﹣=24.
22.(8分)已知:如图,在矩形ABCD中,点E在边AB上,点F在边BC上,且BE=CF,EF⊥DF,求证:BF=CD.
【解答】证明:∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∵EF⊥DF,
∴∠EFD=90°,
∴∠EFB+∠DFC=90°,∠DFC+∠FDC=90°,
∴∠EFB=∠DFC,
∵BE=CF,
∴△BEF≌△CFD,
∴BF=CD.
23.(10分)如图,已知A、B两艘船同时从港口O出发,船A以40km/h的速度向东航行;船B以30km/h的速度向北航行,它们离开港口2h后相距多远?
解:∵A、B两艘船同时从港口O出发,船A以40km/h的速度向东航行;船B以30km/h的速度向北航行,
∴∠AOB=90°,它们离开港口2h后,AO=40×2=80km,BO=30×2=60km,
∴AB==100km,
答:它们离开港口2h后相距100km.
24.(10分)已知,如图,在Rt△ABC中,E是两锐角平分线的交点,ED⊥BC,EF⊥AC,垂足分别为D,F,求证:四边形CDEF是正方形.
【解答】证明:过E作EM⊥AB,
∵AE平分∠CAB,
∴EF=EM,
∵EB平分∠CBA,
∴EM=ED,
∴EF=ED,
∵ED⊥BC,EF⊥AC,△ABC是直角三角形,
∴∠CFE=∠CDE=∠C=90°,
∴四边形EFDC是矩形,
∵EF=ED,
∴四边形CDEF是正方形.
25.(12分)如图,在Rt△ABC中,∠B=90°,AC=40cm,∠A=60°,点D从点C出发沿CA方向以2cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以1cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是a秒(0<a≤20).过点D作DF⊥BC于点F,连接DE,EF.
(1)四边形AEFD能够成为菱形吗?如果能,求出相应的a值;如果不能,请说明理由;
(2)当a为何值时,△DEF为直角三角形?请说明理由.
【解答】(1)证明:能.
理由如下:在△DFC中,∠DFC=90°,∠C=30°,DC=2a,
∴DF=a,
又∵AE=a,
∴AE=DF,
∵AB⊥BC,DF⊥BC,
∴AE∥DF,
又∵AE=DF,
∴四边形AEFD为平行四边形,
当AE=AD时,四边形AEFD为菱形,
即40﹣2a=a,解得a=.
∴当a=秒时,四边形AEFD为菱形.
(2)①当∠DEF=90°时,由(1)知四边形AEFD为平行四边形,
∴EF∥AD,
∴∠ADE=∠DEF=90°,
∵∠A=60°,
∴∠AED=30°,
∴AD=AE=a,
又AD=40﹣2a,即40﹣2a=a,解得a=16;
②当∠EDF=90°时,四边形EBFD为矩形,在Rt△AED中∠A=60°,则∠ADE=30°,
∴AD=2AE,即40﹣2a=2a,解得a=10.
③若∠EFD=90°,则E与B重合,D与A重合,此种情况不存在.
综上所述,当a=16或10秒时,△DEF为直角三角形.
26.(14分)如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作平行四边形ECFG,如图1所示.
(1)证明平行四边形ECFG是菱形;
(2)若∠ABC=120°,连结BG、CG、DG,如图2所示,
①求证:△DGC≌△BGE;
②求∠BDG的度数;
(3)若∠ABC=90°,AB=8,AD=14,M是EF的中点,如图3所示,求DM的长.
解:(1)证明:
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形;
(2)①∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,AD∥BC,
∵∠ABC=120°,
∴∠BCD=60°,∠BCF=120°
由(1)知,四边形CEGF是菱形,
∴CE=GE,∠BCG=∠BCF=60°,
∴CG=GE=CE,∠DCG=120°,
∵EG∥DF,
∴∠BEG=120°=∠DCG,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD,
∴△DGC≌△BGE(SAS);
②∵△DGC≌△BGE,
∴BG=DG,∠BGE=∠DGC,
∴∠BGD=∠CGE,
∵CG=GE=CE,
∴△CEG是等边三角形,
∴∠CGE=60°,
∴∠BGD=60°,
∵BG=DG,
∴△BDG是等边三角形,
∴∠BDG=60°;
(3)方法一:如图3中,连接BM,MC,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵,
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形.
∵AB=8,AD=14,
∴BD=2,
∴DM=BD=.
方法二:过M作MH⊥DF于H,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形,
∴∠CEF=45°,
∴∠AEB=∠CEF=45°,
∴BE=AB=8,
∴CE=CF=14﹣8=6,
∵MH∥CE,EM=FM,
∴CH=FH=CF=3,
∴MH=CE=3,
∴DH=11,
∴DM==.
一、选择题
1.(4分)下列图形是中心对称图形的是( )
A. B.
C. D.
2.(4分)下列各组线段能构成直角三角形的一组是( )
A.9,40,41 B.7,12,13 C.5,9,12 D.3,4,6
3.(4分)已知过一个多边形的一个顶点可以引2条对角线,则它是( )
A.六边形 B.五边形 C.四边形 D.三角形
4.(4分)关于?ABCD的叙述,正确的是( )
A.若AC=BD,则?ABCD是菱形
B.若AB=AD,则?ABCD是矩形
C.若AB⊥BC,则?ABCD是正方形
D.若AC⊥BD,则?ABCD是菱形
5.(4分)菱形的两条对角线分别是12和16,则此菱形的边长是( )
A.10 B.8 C.6 D.5
6.(4分)如图,在△ABC中,AC=10,DE是△ABC的中位线,则DE的长度是( )
A.3 B.4 C.4.8 D.5
7.(4分)如图,菱形ABCD中,∠B=120°,则∠1的度数是( )
A.30° B.25° C.20° D.15°
8.(4分)如图,在Rt△ABC中,CE是斜边AB上的中线,CD⊥AB,若CD=5,CE=6,则△ABC的面积是( )
A.24 B.25 C.30 D.36
9.(4分)如图,正方形纸片ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别沿AE、AF折叠,点B,D恰好都落在点G处,已知BE=1,则EF的长为( )
A.1.5 B.2.5 C.2.25 D.3
10.(4分)如图,矩形ABCD的面积为28,对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1:以AB、AO1为邻边作平行四边形AO1C2B;…,依此类推,则平行四边形AO6C7B的面积为( )
A. B. C. D.
二、填空题(每题4分,共8题)
11.(4分)一个多边形的每一个内角都是120°,则这个多边形是 边形.
12.(4分)直角三角形一条直角边长为8cm,它所对的角为30°,则斜边为 .
13.(4分)如图,在△ABC中,∠C=90°,AD是角平分线,CD=9,则点D到AB的距离为 .
14.(4分)如图,直线l上有三个正方形,A,B,C,若A,C的面积分别为36和64,则B的面积为 .
15.(4分)如图,?ABCD的周长是22,△ABC的周长是17,则AC的长为 .
16.(4分)如图,在平行四边形ABCD中,AB=,AD=4,AC⊥BC.则BD= .
17.(4分)已知四边形ABCD是正方形,以AD为边在正方形ABCD所在平面内作等边三角形PAD,那么∠BPC的度数是 .
18.(4分)如图,在梯形ABCD中,AD∥BC,AD=4,BC=12,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间为 秒时,以点P,Q,E,D为顶点的四边形是平行四边形.
三、解答题(共8题,共78分)
19.(8分)如图,在四边形ABCD中,∠C+∠D=210°
(1)∠DAB+∠CBA= 度;
(2)若∠DAB的角平分线与∠CBA的角平分线相交于点E,求∠E的度数.
20.(8分)如图,已知∠AOB=30°,P是∠AOB平分线上一点,CP∥OB,交OA于点C,PD⊥OB,垂足为点D,且PC=6,求PD的长.(提示:过点P作PE⊥OA于点E)
21.(8分)如图所示的一块地(图中阴影部分)∠ADC=90°,AD=4,CD=3,AB=13,BC=12
(1)求∠ACB的度数;
(2)求阴影部分的面积.
22.(8分)已知:如图,在矩形ABCD中,点E在边AB上,点F在边BC上,且BE=CF,EF⊥DF,求证:BF=CD.
23.(10分)如图,已知A、B两艘船同时从港口O出发,船A以40km/h的速度向东航行;船B以30km/h的速度向北航行,它们离开港口2h后相距多远?
24.(10分)已知,如图,在Rt△ABC中,E是两锐角平分线的交点,ED⊥BC,EF⊥AC,垂足分别为D,F,求证:四边形CDEF是正方形.
25.(12分)如图,在Rt△ABC中,∠B=90°,AC=40cm,∠A=60°,点D从点C出发沿CA方向以2cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以1cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是a秒(0<a≤20).过点D作DF⊥BC于点F,连接DE,EF.
(1)四边形AEFD能够成为菱形吗?如果能,求出相应的a值;如果不能,请说明理由;
(2)当a为何值时,△DEF为直角三角形?请说明理由.
26.(14分)如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作平行四边形ECFG,如图1所示.
(1)证明平行四边形ECFG是菱形;
(2)若∠ABC=120°,连结BG、CG、DG,如图2所示,
①求证:△DGC≌△BGE;
②求∠BDG的度数;
(3)若∠ABC=90°,AB=8,AD=14,M是EF的中点,如图3所示,求DM的长.
参考答案
一.选择题(每小题4分,共10题)
1.(4分)下列图形是中心对称图形的是( )
A. B.
C. D.
解:A、C、D中图形都不是中心对称图形,
B中图形是中心对称图形,
故选:B.
2.(4分)下列各组线段能构成直角三角形的一组是( )
A.9,40,41 B.7,12,13 C.5,9,12 D.3,4,6
解:A、92+402=412,能构成直角三角形;
B、72+122≠132,不能构成直角三角形;
C、52+92≠122,不能构成直角三角形;
D、32+42≠62,不能构成直角三角形.
故选:A.
3.(4分)已知过一个多边形的一个顶点可以引2条对角线,则它是( )
A.六边形 B.五边形 C.四边形 D.三角形
解:设多边形的边数为n.
根据题意得;n﹣3=2.
解得:n=5.
故选:B.
4.(4分)关于?ABCD的叙述,正确的是( )
A.若AC=BD,则?ABCD是菱形
B.若AB=AD,则?ABCD是矩形
C.若AB⊥BC,则?ABCD是正方形
D.若AC⊥BD,则?ABCD是菱形
解:∵?ABCD中,AC=BD,
∴四边形ABCD是矩形,选项A不符合题意;
∵?ABCD中,AB=AD,
∴四边形ABCD是菱形,不一定是正方形,选项B不符合题意;
∵?ABCD中,AB⊥BC,
∴四边形ABCD是矩形,不一定是正方形,选项C不符合题意;
∵?ABCD中,AC⊥BD,
∴四边形ABCD是菱形,选项D符合题意;
故选:D.
5.(4分)菱形的两条对角线分别是12和16,则此菱形的边长是( )
A.10 B.8 C.6 D.5
解:如图,
∵菱形ABCD中,AC=12,BD=16,
∴OA=AC=6,OB=BD=8,AC⊥BD,
∴AB==10.
即菱形的边长是10.
故选:A.
6.(4分)如图,在△ABC中,AC=10,DE是△ABC的中位线,则DE的长度是( )
A.3 B.4 C.4.8 D.5
解:∵DE是△ABC的中位线,
∴DE=AC=×10=5,
故选:D.
7.(4分)如图,菱形ABCD中,∠B=120°,则∠1的度数是( )
A.30° B.25° C.20° D.15°
解:∵四边形ABCD是菱形,
∴AB=BC,
∵∠B=120°,
∴∠1==30°,
故选:A.
8.(4分)如图,在Rt△ABC中,CE是斜边AB上的中线,CD⊥AB,若CD=5,CE=6,则△ABC的面积是( )
A.24 B.25 C.30 D.36
解:∵CE是斜边AB上的中线,
∴AB=2CE=2×6=12,
∴S△ABC=×CD×AB=×5×12=30,
故选:C.
9.(4分)如图,正方形纸片ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别沿AE、AF折叠,点B,D恰好都落在点G处,已知BE=1,则EF的长为( )
A.1.5 B.2.5 C.2.25 D.3
解:∵正方形纸片ABCD的边长为3,
∴∠C=90°,BC=CD=3,
根据折叠的性质得:EG=BE=1,GF=DF,
设DF=x,
则EF=EG+GF=1+x,FC=DC﹣DF=3﹣x,EC=BC﹣BE=3﹣1=2,
∵在Rt△EFC中,EF2=EC2+FC2,即(x+1)2=22+(3﹣x)2,解得:x=1.5,
∴DF=1.5,EF=1+1.5=2.5.
故选:B.
10.(4分)如图,矩形ABCD的面积为28,对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1:以AB、AO1为邻边作平行四边形AO1C2B;…,依此类推,则平行四边形AO6C7B的面积为( )
A. B. C. D.
解:设矩形ABCD的面积为S,
根据题意得:平行四边形AOC1B的面积=矩形ABCD的面积=S,
平行四边形AO1C2B的面积=平行四边形AOC1B的面积=S=,…,
平行四边形AOn﹣1?nB的面积=,
∴平行四边形AOnCn+1B的面积=,
∴平行四边形AO6C7B的面积为==;
故选:C.
二、填空题(每题4分,共8题)
11.(4分)一个多边形的每一个内角都是120°,则这个多边形是 六 边形.
解:180﹣120=60,
多边形的边数是:360÷60=6.
则这个多边形是六边形.
12.(4分)直角三角形一条直角边长为8cm,它所对的角为30°,则斜边为 16cm .
解:如图,在Rt△ABC中,∠B=90°,∠A=30°,BC=8cm,则BC=AC=8cm,
所以AC=2BC=16cm.
故答案是:16cm.
13.(4分)如图,在△ABC中,∠C=90°,AD是角平分线,CD=9,则点D到AB的距离为 9 .
解:如图,过D作DE⊥AB于E,
∵AD是∠BAC的平分线,∠C=90°,
∴DE=DC=9,
即点D到AB的距离为9.
故答案为:9.
14.(4分)如图,直线l上有三个正方形,A,B,C,若A,C的面积分别为36和64,则B的面积为 100 .
解:如图,
∵图形A、B、C都是为正方形,
∴EF2=36,MN2=64,GE=GM,∠EGM=90°,
∴∠EGF+∠NGM=90°,
而∠EGF+∠FEG=90°,
∴∠FEG=∠NGM,
在△EFG和△GNM中,
,
∴△EFG≌△GNM,
∴GF=MN,
在Rt△EFG中,EG2=EF2+FG2=EG2+MN2=36+64=100,
∴正方形B的面积为100.
故答案为100.
15.(4分)如图,?ABCD的周长是22,△ABC的周长是17,则AC的长为 6 .
解:∵,?ABCD的周长是22,
∴AB+BC=11,
∵△ABC的周长是17,
∴AC=17﹣11=6,
故答案为:6
16.(4分)如图,在平行四边形ABCD中,AB=,AD=4,AC⊥BC.则BD= 10 .
解:∵四边形ABCD是平行四边形,
∴BC=AD=4,OB=OD,OA=OC,
∵AC⊥BC,
∴由勾股定理得:AC===6,
∴OC=AC=3,
∵在Rt△BCO中,∠BCO=90°,
∴OB===5,
∴BD=2OB=10,
故答案为:10.
17.(4分)已知四边形ABCD是正方形,以AD为边在正方形ABCD所在平面内作等边三角形PAD,那么∠BPC的度数是 30°或150° .
解:如图(1),
∵四边形ABCD是正方形,△PAD是等边三角形,
∴∠BAP=∠BAD+∠PAB=90°+60°=150°.
∵PA=AD,AB=AD,
∴PA=AB,
∴∠ABP=(180°﹣150°)=15°,
∴∠PBC=∠ABC﹣∠ABP=90°﹣15°=75°,
同理:∠PCB=75°,
∴∠BPC=180°﹣75°﹣75°=30°.
如图(2),∵四边形ABCD是正方形,△PAD是等边三角形,
∴∠BAP=∠BAD﹣∠PAB=90°﹣60°=30°.
∵PA=AD,AB=AD,
∴PA=AB,
∴∠APB=(180°﹣30°)=75°,
同理:∠CPD=75°,
∴∠BPC=360°﹣75°﹣75°﹣60°=150°.
综上可得:∠BPC的度数是30°或150°.
故答案为:30°或150°.
18.(4分)如图,在梯形ABCD中,AD∥BC,AD=4,BC=12,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间为 2或 秒时,以点P,Q,E,D为顶点的四边形是平行四边形.
解:∵E是BC的中点,
∴BE=CE=BC=×12=6,
①当Q运动到E和C之间,设运动时间为t,则AP=t,DP=AD﹣AP=4﹣t,CQ=2t,EQ=CE﹣CQ=6﹣2t,
∴4﹣t=6﹣2t,
解得:t=2;
②当Q运动到E和B之间,设运动时间为t,则AP=t,DP=AD﹣AP=4﹣t,CQ=2t,EQ=CQ﹣CE=2t﹣6,
∴4﹣t=2t﹣6,
解得:t=,
∴当运动时间t为2或秒时,以点P,Q,E,D为顶点的四边形是平行四边形.
故答案为:2或.
三、解答题(共8题,共78分)
19.(8分)如图,在四边形ABCD中,∠C+∠D=210°
(1)∠DAB+∠CBA= 150 度;
(2)若∠DAB的角平分线与∠CBA的角平分线相交于点E,求∠E的度数.
解:(1)∵∠DAB+∠CBA+∠C+∠D=360°,
∴∠DAB+∠CBA=360°﹣(∠C+∠D)=360°﹣210°=150°.
故答案为:150;
(2)∵∠DAB与∠ABC的平分线交于四边形内一点E,
∴∠EAB=∠DAB,∠EBA=∠ABC,
∴∠E=180°﹣(∠EAB+∠EBA)
=180°﹣(∠DAB+∠CBA)
=180°﹣(360°﹣∠C﹣∠D)
=(∠C+∠D),
∵∠C+∠D=210°,
∴∠E=(∠C+∠D)=105°.
20.(8分)如图,已知∠AOB=30°,P是∠AOB平分线上一点,CP∥OB,交OA于点C,PD⊥OB,垂足为点D,且PC=6,求PD的长.(提示:过点P作PE⊥OA于点E)
解:过点P作PE⊥OA于点E,如图所示,
∵OP平分∠AOB,PD⊥OB,PE⊥OA,∠AOB=30°,
∴∠COP=∠POD=15°,PD=PE,
∵CP∥OB,
∴∠POD=∠CPO,
∴∠COP+∠CPO=∠COP+∠POD=30°,
∴∠ECP=∠COP+∠CPO=30°,
∵PC=6,∠PEC=90°,
∴PE=3,
∴PD=3.
21.(8分)如图所示的一块地(图中阴影部分)∠ADC=90°,AD=4,CD=3,AB=13,BC=12
(1)求∠ACB的度数;
(2)求阴影部分的面积.
解:(1)在Rt△ADC中,由勾股定理得:AC===5,
∵AB=13,BC=12,AC=5,
∴AC2+BC2=AB2,
∴∠ACB=90°;
(2)阴影部分的面积S=S△ACB﹣S△ADC=﹣=24.
22.(8分)已知:如图,在矩形ABCD中,点E在边AB上,点F在边BC上,且BE=CF,EF⊥DF,求证:BF=CD.
【解答】证明:∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∵EF⊥DF,
∴∠EFD=90°,
∴∠EFB+∠DFC=90°,∠DFC+∠FDC=90°,
∴∠EFB=∠DFC,
∵BE=CF,
∴△BEF≌△CFD,
∴BF=CD.
23.(10分)如图,已知A、B两艘船同时从港口O出发,船A以40km/h的速度向东航行;船B以30km/h的速度向北航行,它们离开港口2h后相距多远?
解:∵A、B两艘船同时从港口O出发,船A以40km/h的速度向东航行;船B以30km/h的速度向北航行,
∴∠AOB=90°,它们离开港口2h后,AO=40×2=80km,BO=30×2=60km,
∴AB==100km,
答:它们离开港口2h后相距100km.
24.(10分)已知,如图,在Rt△ABC中,E是两锐角平分线的交点,ED⊥BC,EF⊥AC,垂足分别为D,F,求证:四边形CDEF是正方形.
【解答】证明:过E作EM⊥AB,
∵AE平分∠CAB,
∴EF=EM,
∵EB平分∠CBA,
∴EM=ED,
∴EF=ED,
∵ED⊥BC,EF⊥AC,△ABC是直角三角形,
∴∠CFE=∠CDE=∠C=90°,
∴四边形EFDC是矩形,
∵EF=ED,
∴四边形CDEF是正方形.
25.(12分)如图,在Rt△ABC中,∠B=90°,AC=40cm,∠A=60°,点D从点C出发沿CA方向以2cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以1cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是a秒(0<a≤20).过点D作DF⊥BC于点F,连接DE,EF.
(1)四边形AEFD能够成为菱形吗?如果能,求出相应的a值;如果不能,请说明理由;
(2)当a为何值时,△DEF为直角三角形?请说明理由.
【解答】(1)证明:能.
理由如下:在△DFC中,∠DFC=90°,∠C=30°,DC=2a,
∴DF=a,
又∵AE=a,
∴AE=DF,
∵AB⊥BC,DF⊥BC,
∴AE∥DF,
又∵AE=DF,
∴四边形AEFD为平行四边形,
当AE=AD时,四边形AEFD为菱形,
即40﹣2a=a,解得a=.
∴当a=秒时,四边形AEFD为菱形.
(2)①当∠DEF=90°时,由(1)知四边形AEFD为平行四边形,
∴EF∥AD,
∴∠ADE=∠DEF=90°,
∵∠A=60°,
∴∠AED=30°,
∴AD=AE=a,
又AD=40﹣2a,即40﹣2a=a,解得a=16;
②当∠EDF=90°时,四边形EBFD为矩形,在Rt△AED中∠A=60°,则∠ADE=30°,
∴AD=2AE,即40﹣2a=2a,解得a=10.
③若∠EFD=90°,则E与B重合,D与A重合,此种情况不存在.
综上所述,当a=16或10秒时,△DEF为直角三角形.
26.(14分)如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作平行四边形ECFG,如图1所示.
(1)证明平行四边形ECFG是菱形;
(2)若∠ABC=120°,连结BG、CG、DG,如图2所示,
①求证:△DGC≌△BGE;
②求∠BDG的度数;
(3)若∠ABC=90°,AB=8,AD=14,M是EF的中点,如图3所示,求DM的长.
解:(1)证明:
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形;
(2)①∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,AD∥BC,
∵∠ABC=120°,
∴∠BCD=60°,∠BCF=120°
由(1)知,四边形CEGF是菱形,
∴CE=GE,∠BCG=∠BCF=60°,
∴CG=GE=CE,∠DCG=120°,
∵EG∥DF,
∴∠BEG=120°=∠DCG,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD,
∴△DGC≌△BGE(SAS);
②∵△DGC≌△BGE,
∴BG=DG,∠BGE=∠DGC,
∴∠BGD=∠CGE,
∵CG=GE=CE,
∴△CEG是等边三角形,
∴∠CGE=60°,
∴∠BGD=60°,
∵BG=DG,
∴△BDG是等边三角形,
∴∠BDG=60°;
(3)方法一:如图3中,连接BM,MC,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵,
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形.
∵AB=8,AD=14,
∴BD=2,
∴DM=BD=.
方法二:过M作MH⊥DF于H,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形,
∴∠CEF=45°,
∴∠AEB=∠CEF=45°,
∴BE=AB=8,
∴CE=CF=14﹣8=6,
∵MH∥CE,EM=FM,
∴CH=FH=CF=3,
∴MH=CE=3,
∴DH=11,
∴DM==.
同课章节目录
