2019-2020学年湖南省株洲五中八年级下学期期中数学试卷 (word版,含解析)
文档属性
| 名称 | 2019-2020学年湖南省株洲五中八年级下学期期中数学试卷 (word版,含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 942.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-03 00:00:00 | ||
图片预览




文档简介
2019-2020学年湖南省株洲五中八年级第二学期期中数学试卷
一、选择题
1.(4分)京剧脸谱、剪纸等图案蕴含着对称美,下面选取的图案中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.(4分)下列四组线段中,能组成直角三角形的是( )
A.a=1,b=2,c=3 B.a=2,b=3,c=4
C.a=2,b=4,c=5 D.a=3,b=4,c=5
3.(4分)一个多边形内角和是1080°,则这个多边形是( )
A.六边形 B.七边形 C.八边形 D.九边形
4.(4分)如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开.若测得AM的长为1.2km,则M,C两点间的距离为( )
A.0.5km B.0.6km C.0.9km D.1.2km
5.(4分)如图,一辆货车车厢底板离地面的高度为米,为了方便下货,常用一块木板搭成一个斜面,要使斜面与水平地面的夹角不大于30°,则这块木板的长度至少为( )
A.3米 B.2.5米 C.2.6米 D.0.87米
6.(4分)点P在第二象限内,若P到x轴的距离是3,到y轴的距离是4,那么点P的坐标为( )
A.(﹣4,3) B.(﹣3,﹣4) C.(﹣3,4) D.(3,﹣4)
7.(4分)若点M(a﹣2,2a+3)是y轴上的点,则a的值是( )
A.2 B.﹣ C.﹣2 D.
8.(4分)菱形具有而矩形不一定具有的性质是( )
A.对角相等且互补
B.对角线互相平分
C.一组对边平行,另一组对边相等
D.对角线互相垂直
9.(4分)如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,以A为圆心,AB为半径的弧交AD于点F,连接EF.若BF=6,AB=5,则四边形ABEF面积是( )
A.12 B.24 C.36 D.48
10.(4分)如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长交BC于点G,连接AG.则BG的长( )
A.1 B.2 C. D.3
二、填空题(本题共8小题,每小题4分,共32分)
11.(4分)在平面直角坐标系中,点(﹣2,﹣3)在第 象限.
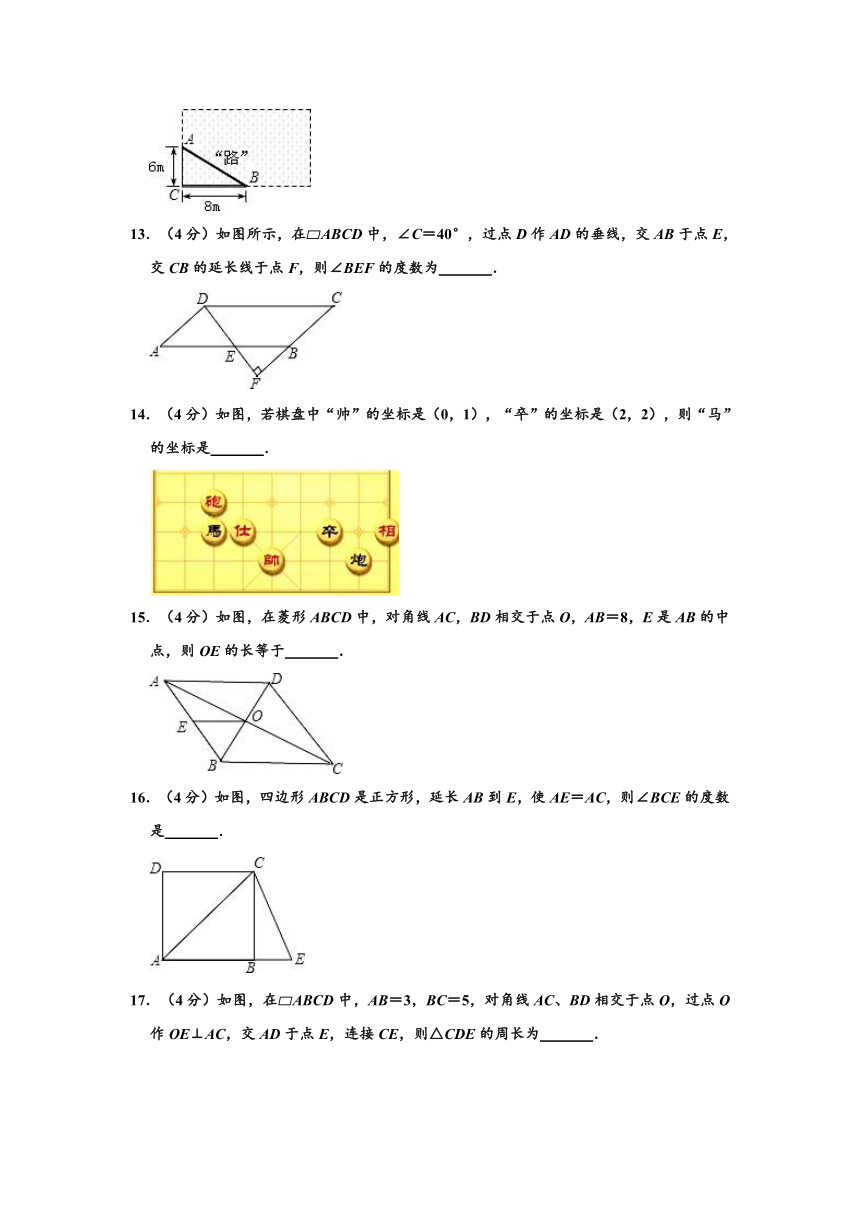
12.(4分)如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了 步路(假设2步为1米),却踩伤了花草.
13.(4分)如图所示,在?ABCD中,∠C=40°,过点D作AD的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为 .
14.(4分)如图,若棋盘中“帅”的坐标是(0,1),“卒”的坐标是(2,2),则“马”的坐标是 .
15.(4分)如图,在菱形ABCD中,对角线AC,BD相交于点O,AB=8,E是AB的中点,则OE的长等于 .
16.(4分)如图,四边形ABCD是正方形,延长AB到E,使AE=AC,则∠BCE的度数是 .
17.(4分)如图,在?ABCD中,AB=3,BC=5,对角线AC、BD相交于点O,过点O作OE⊥AC,交AD于点E,连接CE,则△CDE的周长为 .
18.(4分)如图的平面直角坐标系中,已知点A(﹣3,0)、B(0,4),将△OAB沿x轴作连续无滑动的翻滚,依次得到三角形①,②,③,④..则第?个三角形的直角顶点的坐标是 .
三、解答题(本大题共8小题,共78分)
19.(8分)在边长为1的小正方形网格中,△AOB的顶点均在格点上,
(1)B点关于y轴的对称点坐标为 ;
(2)将△AOB向左平移4个单位长度得到△A1O1B1,请画出△A1O1B1.
20.(8分)如图,四边形ABCD中,AD∥BC,对角线AC,BD交于点O,且OA=OC,求证:四边形ABCD是平行四边形.
21.(8分)游艇在湖面上以12千米/小时的速度向正东方向航行,在O处看到灯塔A在游艇北偏东60°方向上,航行1小时到达B处,此时看到灯塔A在游艇北偏西30°方向上,求此时游艇与灯塔的距离AB.
22.(8分)如图,在平行四边形ABCD中,点P是对角线AC上的一点,PE⊥AB,PF⊥AD,垂足分别为E、F,且PE=PF,平行四边形ABCD是菱形吗?为什么?
23.(10分)如图,在?ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°.求∠B的度数.
24.(10分)在?ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
25.(13分)如图所示,在四边形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C出发沿着CB方向向点B以3cm/s的速度运动.点P,Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.
(1)经过多长时间,四边形PQCD是平行四边形?
(2)经过多长时间,四边形PQBA是矩形?
(3)若AB=8,如果Q点的移动速度不变,要使PQBA是正方形,则P点移动速度是多少?
26.(13分)如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
参考答案
一、选择题(每小题有且只有一个正确答案,本题共10小题,每小题4分,共40分)
1.(4分)京剧脸谱、剪纸等图案蕴含着对称美,下面选取的图案中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
解:A、是轴对称图形,不是中心对称图形,故此选项不合题意;
B、既不是轴对称图形,也不是中心对称图形,故此选项不合题意;
C、不是轴对称图形,是中心对称图形,故此选项不合题意;
D、既是轴对称图形,也是中心对称图形,故此选项符合题意;
故选:D.
2.(4分)下列四组线段中,能组成直角三角形的是( )
A.a=1,b=2,c=3 B.a=2,b=3,c=4
C.a=2,b=4,c=5 D.a=3,b=4,c=5
解:A、∵12+22=5≠32,∴不能构成直角三角形,故本选项错误;
B、∵22+32=13≠42,∴不能构成直角三角形,故本选项错误;
C、∵22+42=20≠52,∴不能构成直角三角形,故本选项错误;
D、∵32+42=25=52,∴能构成直角三角形,故本选项正确.
故选:D.
3.(4分)一个多边形内角和是1080°,则这个多边形是( )
A.六边形 B.七边形 C.八边形 D.九边形
解:设这个多边形是n边形,由题意知,
(n﹣2)×180°=1080°,
∴n=8,
所以该多边形的边数是八边形.
故选:C.
4.(4分)如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开.若测得AM的长为1.2km,则M,C两点间的距离为( )
A.0.5km B.0.6km C.0.9km D.1.2km
解:∵在Rt△ABC中,∠ACB=90°,M为AB的中点,
∴MC=AB=AM=1.2km.
故选:D.
5.(4分)如图,一辆货车车厢底板离地面的高度为米,为了方便下货,常用一块木板搭成一个斜面,要使斜面与水平地面的夹角不大于30°,则这块木板的长度至少为( )
A.3米 B.2.5米 C.2.6米 D.0.87米
解:如图:AC为车厢底板离地面的高度米,
AB是要求木板的长度,
因为在直角三角形ABC中,∠B=30°,
所以AB=2AC=2×=3(米).
故选:A.
6.(4分)点P在第二象限内,若P到x轴的距离是3,到y轴的距离是4,那么点P的坐标为( )
A.(﹣4,3) B.(﹣3,﹣4) C.(﹣3,4) D.(3,﹣4)
解:∵点P在第二象限内,
∴点P的横坐标小于0,纵坐标大于0,
又∵P到x轴的距离是3,到y轴的距离是4可知,
∴点P的横坐标是﹣4,纵坐标是3,即点P的坐标为(﹣4,3).故选A.
7.(4分)若点M(a﹣2,2a+3)是y轴上的点,则a的值是( )
A.2 B.﹣ C.﹣2 D.
解:∵点M(a﹣2,2a+3)是y轴上的点,
∴a﹣2=0,
解得:a=2,
故选:A.
8.(4分)菱形具有而矩形不一定具有的性质是( )
A.对角相等且互补
B.对角线互相平分
C.一组对边平行,另一组对边相等
D.对角线互相垂直
解:菱形的性质有:对边平行且相等;对角相等,邻角互补;对角线互相垂直平分;
矩形的性质有:对边平行且相等;四个角都是直角;对角线互相平分;
根据菱形和矩形的性质得出:菱形具有而矩形不一定具有的性质是对角线互相垂直;
故选:D.
9.(4分)如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,以A为圆心,AB为半径的弧交AD于点F,连接EF.若BF=6,AB=5,则四边形ABEF面积是( )
A.12 B.24 C.36 D.48
解:连接EF,AE与BF相交于O点,如图,
由作法得AB=AF=10,AE平分∠BAD,
∴∠BAE=∠DAE,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠DAE=∠BEA,
∴∠BAE=∠BEA,
∴BA=BE,
∴AF=BE,
而AF∥BE,
∴四边形ABEF为平行四边形,
而AB=AF,
∴四边形ABEF为菱形,
∴OA=OE,OB=OF=BF=3,AE⊥BF,
在Rt△AOB中,OA==4,
∴AE=2AO=8,
∴四边形ABEF面积=×AE×BF=×6×8=24.
故选:B.
10.(4分)如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长交BC于点G,连接AG.则BG的长( )
A.1 B.2 C. D.3
解:∵E是边CD的中点,正方形ABCD的边长为6,
∴DE=EC=3,
∵△ADE沿AE对折至△AFE,
∴EF=DE=3,AF=AD=6,
∴AB=AF=6,
在Rt△ABG和Rt△AFG中,,
∴Rt△ABG≌Rt△AFG(HL),
∴BG=FG,
设BG=x,则CG=6﹣x,EG=3+x,
在Rt△CGE中,由勾股定理得,CG2+EC2=EG2,
即(6﹣x)2+32=(3+x)2,
解得x=2,
即BG=2.
故选:B.
二、填空题(本题共8小题,每小题4分,共32分)
11.(4分)在平面直角坐标系中,点(﹣2,﹣3)在第 三 象限.
解:∵点的横纵坐标均为负数,
∴点(﹣2,﹣3)在第三象限.
故答案为:三.
12.(4分)如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了 8 步路(假设2步为1米),却踩伤了花草.
解:由题意可得:AB==10(m),
则AC+BC﹣AB=14﹣10=4(m),
故他们仅仅少走了:4×2=8(步).
故答案为:8.
13.(4分)如图所示,在?ABCD中,∠C=40°,过点D作AD的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为 50° .
解:∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠C=∠ABF.
又∵∠C=40°,
∴∠ABF=40°.
∵EF⊥BF,
∴∠F=90°,
∴∠BEF=90°﹣40°=50°.
故答案是:50°.
14.(4分)如图,若棋盘中“帅”的坐标是(0,1),“卒”的坐标是(2,2),则“马”的坐标是 (﹣2,2) .
解:根据题意可建立如图所示的平面直角坐标系,
则“马”的坐标是(﹣2,2),
故答案为:(﹣2,2).
15.(4分)如图,在菱形ABCD中,对角线AC,BD相交于点O,AB=8,E是AB的中点,则OE的长等于 4 .
解:∵在菱形ABCD中,AB=8,
∴BC=AB=8,OA=OC,
∵E是AB的中点,
∴OE是△ABC的中位线,
∴OE=BC=4.
故答案为:4.
16.(4分)如图,四边形ABCD是正方形,延长AB到E,使AE=AC,则∠BCE的度数是 22.5° .
解:∵四边形ABCD是正方形,
∴∠BAC=∠ACB=45°,
∵AE=AC,
∴∠ACE=∠E==67.5°,
∴∠BCE=∠ACE﹣∠ACB=67.5°﹣45°=22.5°.
故答案为:22.5°.
17.(4分)如图,在?ABCD中,AB=3,BC=5,对角线AC、BD相交于点O,过点O作OE⊥AC,交AD于点E,连接CE,则△CDE的周长为 8 .
解:根据平行四边形的性质,
∴AO=OC,
∵OE⊥AC,
∴OE为AC的垂直平分线,
∴AE=EC,
∴△CDE的周长为:CD+AD=5+3=8,
故答案为:8.
18.(4分)如图的平面直角坐标系中,已知点A(﹣3,0)、B(0,4),将△OAB沿x轴作连续无滑动的翻滚,依次得到三角形①,②,③,④..则第?个三角形的直角顶点的坐标是 (60,0) .
解:∵点B(﹣3,0),A(0,4),
∴OB=3,OA=4,
∴AB==5,
∵对△OAB连续作如图所示的旋转变换,
∴△OAB每三次旋转后回到原来的状态,并且每三次向前移动了3+4+5=12个单位,
而7=3×2+1,
∴第⑦个三角形和第①个三角形的状态一样,则三角形⑦与三角形⑥的直角顶点相同,
∴三角形⑦的直角顶点的横坐标为2×12=24,纵坐标为0;
由题意可得:第16个三角形与第1个三角形状态相同,直角顶点的坐标为:(60,0),
故答案为(60,0).
三、解答题(本大题共8小题,共78分)
19.(8分)在边长为1的小正方形网格中,△AOB的顶点均在格点上,
(1)B点关于y轴的对称点坐标为 (﹣3,2) ;
(2)将△AOB向左平移4个单位长度得到△A1O1B1,请画出△A1O1B1.
解:(1)由图可知:
点B的坐标是(3,2)
所以B点关于y轴的对称点坐标为(﹣3,2);
故答案为:(﹣3,2);
(2)如图,△A1O1B1即为所求.
20.(8分)如图,四边形ABCD中,AD∥BC,对角线AC,BD交于点O,且OA=OC,求证:四边形ABCD是平行四边形.
【解答】证明:∵AD∥BC,
∴∠OAD=∠OCB,∠ADO=∠BCO.
又OA=OC,
∴△AOD≌△BOC.
∴OA=OC,OB=OD.
∴四边形ABCD为平行四边形.
21.(8分)游艇在湖面上以12千米/小时的速度向正东方向航行,在O处看到灯塔A在游艇北偏东60°方向上,航行1小时到达B处,此时看到灯塔A在游艇北偏西30°方向上,求此时游艇与灯塔的距离AB.
解:过点A作AC⊥OB交OB于C,则AC为所求,设AC=x,
由题意得:OB=12千米,∠AOC=30°,∠ABC=60°,
在Rt△ACO和Rt△ACB中:
tan30°=,tan60°=,
则OC=x,BC=x,
而OC+CB=x+x=12,
解得:x=3.
故AB===6(千米),
答:此时游艇与灯塔的距离AB为6千米.
22.(8分)如图,在平行四边形ABCD中,点P是对角线AC上的一点,PE⊥AB,PF⊥AD,垂足分别为E、F,且PE=PF,平行四边形ABCD是菱形吗?为什么?
解:是菱形.
理由如下:∵PE⊥AB,PF⊥AD,且PE=PF,
∴AC是∠DAB的角平分线,
∴∠DAC=∠CAE,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠DCA=∠CAB,
∴∠DAC=∠DCA,
∴DA=DC,
∴平行四边形ABCD是菱形.
23.(10分)如图,在?ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°.求∠B的度数.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠D=∠ECF,
在△ADE和△FCE中,,
∴△ADE≌△FCE(ASA);
(2)解:∵△ADE≌△FCE,
∴AD=FC,
∵AD=BC,AB=2BC,
∴AB=FB,
∴∠BAF=∠F=36°,
∴∠B=180°﹣2×36°=108°.
24.(10分)在?ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD.
∵BE∥DF,BE=DF,
∴四边形BFDE是平行四边形.
∵DE⊥AB,
∴∠DEB=90°,
∴四边形BFDE是矩形;
(2)∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠DFA=∠FAB.
在Rt△BCF中,由勾股定理,得
BC==5,
∴AD=BC=DF=5,
∴∠DAF=∠DFA,
∴∠DAF=∠FAB,
即AF平分∠DAB.
25.(13分)如图所示,在四边形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C出发沿着CB方向向点B以3cm/s的速度运动.点P,Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.
(1)经过多长时间,四边形PQCD是平行四边形?
(2)经过多长时间,四边形PQBA是矩形?
(3)若AB=8,如果Q点的移动速度不变,要使PQBA是正方形,则P点移动速度是多少?
解:(1)当PD=CQ时,四边形PQCD是平行四边形,设运动时间为ts.
∴24﹣t=3t,
解得t=6.
∴6s时,四边形PQCD是平行四边形.
(2)当AP=BQ时,四边形PQBA是矩形,设运动时间为ts.
∴t=26﹣3t,
解得t=,
∴s时,四边形PQBA是矩形.
(3)设运动时间为ts.当BQ=AB=8时,26﹣3t=8,
∴t=6,
∵PA=6?VP=8,
∴VP=cm/s.
26.(13分)如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
【解答】(1)证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
(2)解:四边形BECD是菱形,
理由是:∵D为AB中点,
∴AD=BD,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=BD(直角三角形斜边上的中线等于斜边的一半),
∴四边形BECD是菱形;
(3)当∠A=45°时,四边形BECD是正方形,理由是:
解:∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°,
∴AC=BC,
∵D为BA中点,
∴CD⊥AB,
∴∠CDB=90°,
∵四边形BECD是菱形,
∴菱形BECD是正方形,
即当∠A=45°时,四边形BECD是正方形.
一、选择题
1.(4分)京剧脸谱、剪纸等图案蕴含着对称美,下面选取的图案中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.(4分)下列四组线段中,能组成直角三角形的是( )
A.a=1,b=2,c=3 B.a=2,b=3,c=4
C.a=2,b=4,c=5 D.a=3,b=4,c=5
3.(4分)一个多边形内角和是1080°,则这个多边形是( )
A.六边形 B.七边形 C.八边形 D.九边形
4.(4分)如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开.若测得AM的长为1.2km,则M,C两点间的距离为( )
A.0.5km B.0.6km C.0.9km D.1.2km
5.(4分)如图,一辆货车车厢底板离地面的高度为米,为了方便下货,常用一块木板搭成一个斜面,要使斜面与水平地面的夹角不大于30°,则这块木板的长度至少为( )
A.3米 B.2.5米 C.2.6米 D.0.87米
6.(4分)点P在第二象限内,若P到x轴的距离是3,到y轴的距离是4,那么点P的坐标为( )
A.(﹣4,3) B.(﹣3,﹣4) C.(﹣3,4) D.(3,﹣4)
7.(4分)若点M(a﹣2,2a+3)是y轴上的点,则a的值是( )
A.2 B.﹣ C.﹣2 D.
8.(4分)菱形具有而矩形不一定具有的性质是( )
A.对角相等且互补
B.对角线互相平分
C.一组对边平行,另一组对边相等
D.对角线互相垂直
9.(4分)如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,以A为圆心,AB为半径的弧交AD于点F,连接EF.若BF=6,AB=5,则四边形ABEF面积是( )
A.12 B.24 C.36 D.48
10.(4分)如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长交BC于点G,连接AG.则BG的长( )
A.1 B.2 C. D.3
二、填空题(本题共8小题,每小题4分,共32分)
11.(4分)在平面直角坐标系中,点(﹣2,﹣3)在第 象限.
12.(4分)如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了 步路(假设2步为1米),却踩伤了花草.
13.(4分)如图所示,在?ABCD中,∠C=40°,过点D作AD的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为 .
14.(4分)如图,若棋盘中“帅”的坐标是(0,1),“卒”的坐标是(2,2),则“马”的坐标是 .
15.(4分)如图,在菱形ABCD中,对角线AC,BD相交于点O,AB=8,E是AB的中点,则OE的长等于 .
16.(4分)如图,四边形ABCD是正方形,延长AB到E,使AE=AC,则∠BCE的度数是 .
17.(4分)如图,在?ABCD中,AB=3,BC=5,对角线AC、BD相交于点O,过点O作OE⊥AC,交AD于点E,连接CE,则△CDE的周长为 .
18.(4分)如图的平面直角坐标系中,已知点A(﹣3,0)、B(0,4),将△OAB沿x轴作连续无滑动的翻滚,依次得到三角形①,②,③,④..则第?个三角形的直角顶点的坐标是 .
三、解答题(本大题共8小题,共78分)
19.(8分)在边长为1的小正方形网格中,△AOB的顶点均在格点上,
(1)B点关于y轴的对称点坐标为 ;
(2)将△AOB向左平移4个单位长度得到△A1O1B1,请画出△A1O1B1.
20.(8分)如图,四边形ABCD中,AD∥BC,对角线AC,BD交于点O,且OA=OC,求证:四边形ABCD是平行四边形.
21.(8分)游艇在湖面上以12千米/小时的速度向正东方向航行,在O处看到灯塔A在游艇北偏东60°方向上,航行1小时到达B处,此时看到灯塔A在游艇北偏西30°方向上,求此时游艇与灯塔的距离AB.
22.(8分)如图,在平行四边形ABCD中,点P是对角线AC上的一点,PE⊥AB,PF⊥AD,垂足分别为E、F,且PE=PF,平行四边形ABCD是菱形吗?为什么?
23.(10分)如图,在?ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°.求∠B的度数.
24.(10分)在?ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
25.(13分)如图所示,在四边形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C出发沿着CB方向向点B以3cm/s的速度运动.点P,Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.
(1)经过多长时间,四边形PQCD是平行四边形?
(2)经过多长时间,四边形PQBA是矩形?
(3)若AB=8,如果Q点的移动速度不变,要使PQBA是正方形,则P点移动速度是多少?
26.(13分)如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
参考答案
一、选择题(每小题有且只有一个正确答案,本题共10小题,每小题4分,共40分)
1.(4分)京剧脸谱、剪纸等图案蕴含着对称美,下面选取的图案中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
解:A、是轴对称图形,不是中心对称图形,故此选项不合题意;
B、既不是轴对称图形,也不是中心对称图形,故此选项不合题意;
C、不是轴对称图形,是中心对称图形,故此选项不合题意;
D、既是轴对称图形,也是中心对称图形,故此选项符合题意;
故选:D.
2.(4分)下列四组线段中,能组成直角三角形的是( )
A.a=1,b=2,c=3 B.a=2,b=3,c=4
C.a=2,b=4,c=5 D.a=3,b=4,c=5
解:A、∵12+22=5≠32,∴不能构成直角三角形,故本选项错误;
B、∵22+32=13≠42,∴不能构成直角三角形,故本选项错误;
C、∵22+42=20≠52,∴不能构成直角三角形,故本选项错误;
D、∵32+42=25=52,∴能构成直角三角形,故本选项正确.
故选:D.
3.(4分)一个多边形内角和是1080°,则这个多边形是( )
A.六边形 B.七边形 C.八边形 D.九边形
解:设这个多边形是n边形,由题意知,
(n﹣2)×180°=1080°,
∴n=8,
所以该多边形的边数是八边形.
故选:C.
4.(4分)如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开.若测得AM的长为1.2km,则M,C两点间的距离为( )
A.0.5km B.0.6km C.0.9km D.1.2km
解:∵在Rt△ABC中,∠ACB=90°,M为AB的中点,
∴MC=AB=AM=1.2km.
故选:D.
5.(4分)如图,一辆货车车厢底板离地面的高度为米,为了方便下货,常用一块木板搭成一个斜面,要使斜面与水平地面的夹角不大于30°,则这块木板的长度至少为( )
A.3米 B.2.5米 C.2.6米 D.0.87米
解:如图:AC为车厢底板离地面的高度米,
AB是要求木板的长度,
因为在直角三角形ABC中,∠B=30°,
所以AB=2AC=2×=3(米).
故选:A.
6.(4分)点P在第二象限内,若P到x轴的距离是3,到y轴的距离是4,那么点P的坐标为( )
A.(﹣4,3) B.(﹣3,﹣4) C.(﹣3,4) D.(3,﹣4)
解:∵点P在第二象限内,
∴点P的横坐标小于0,纵坐标大于0,
又∵P到x轴的距离是3,到y轴的距离是4可知,
∴点P的横坐标是﹣4,纵坐标是3,即点P的坐标为(﹣4,3).故选A.
7.(4分)若点M(a﹣2,2a+3)是y轴上的点,则a的值是( )
A.2 B.﹣ C.﹣2 D.
解:∵点M(a﹣2,2a+3)是y轴上的点,
∴a﹣2=0,
解得:a=2,
故选:A.
8.(4分)菱形具有而矩形不一定具有的性质是( )
A.对角相等且互补
B.对角线互相平分
C.一组对边平行,另一组对边相等
D.对角线互相垂直
解:菱形的性质有:对边平行且相等;对角相等,邻角互补;对角线互相垂直平分;
矩形的性质有:对边平行且相等;四个角都是直角;对角线互相平分;
根据菱形和矩形的性质得出:菱形具有而矩形不一定具有的性质是对角线互相垂直;
故选:D.
9.(4分)如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,以A为圆心,AB为半径的弧交AD于点F,连接EF.若BF=6,AB=5,则四边形ABEF面积是( )
A.12 B.24 C.36 D.48
解:连接EF,AE与BF相交于O点,如图,
由作法得AB=AF=10,AE平分∠BAD,
∴∠BAE=∠DAE,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠DAE=∠BEA,
∴∠BAE=∠BEA,
∴BA=BE,
∴AF=BE,
而AF∥BE,
∴四边形ABEF为平行四边形,
而AB=AF,
∴四边形ABEF为菱形,
∴OA=OE,OB=OF=BF=3,AE⊥BF,
在Rt△AOB中,OA==4,
∴AE=2AO=8,
∴四边形ABEF面积=×AE×BF=×6×8=24.
故选:B.
10.(4分)如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长交BC于点G,连接AG.则BG的长( )
A.1 B.2 C. D.3
解:∵E是边CD的中点,正方形ABCD的边长为6,
∴DE=EC=3,
∵△ADE沿AE对折至△AFE,
∴EF=DE=3,AF=AD=6,
∴AB=AF=6,
在Rt△ABG和Rt△AFG中,,
∴Rt△ABG≌Rt△AFG(HL),
∴BG=FG,
设BG=x,则CG=6﹣x,EG=3+x,
在Rt△CGE中,由勾股定理得,CG2+EC2=EG2,
即(6﹣x)2+32=(3+x)2,
解得x=2,
即BG=2.
故选:B.
二、填空题(本题共8小题,每小题4分,共32分)
11.(4分)在平面直角坐标系中,点(﹣2,﹣3)在第 三 象限.
解:∵点的横纵坐标均为负数,
∴点(﹣2,﹣3)在第三象限.
故答案为:三.
12.(4分)如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了 8 步路(假设2步为1米),却踩伤了花草.
解:由题意可得:AB==10(m),
则AC+BC﹣AB=14﹣10=4(m),
故他们仅仅少走了:4×2=8(步).
故答案为:8.
13.(4分)如图所示,在?ABCD中,∠C=40°,过点D作AD的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为 50° .
解:∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠C=∠ABF.
又∵∠C=40°,
∴∠ABF=40°.
∵EF⊥BF,
∴∠F=90°,
∴∠BEF=90°﹣40°=50°.
故答案是:50°.
14.(4分)如图,若棋盘中“帅”的坐标是(0,1),“卒”的坐标是(2,2),则“马”的坐标是 (﹣2,2) .
解:根据题意可建立如图所示的平面直角坐标系,
则“马”的坐标是(﹣2,2),
故答案为:(﹣2,2).
15.(4分)如图,在菱形ABCD中,对角线AC,BD相交于点O,AB=8,E是AB的中点,则OE的长等于 4 .
解:∵在菱形ABCD中,AB=8,
∴BC=AB=8,OA=OC,
∵E是AB的中点,
∴OE是△ABC的中位线,
∴OE=BC=4.
故答案为:4.
16.(4分)如图,四边形ABCD是正方形,延长AB到E,使AE=AC,则∠BCE的度数是 22.5° .
解:∵四边形ABCD是正方形,
∴∠BAC=∠ACB=45°,
∵AE=AC,
∴∠ACE=∠E==67.5°,
∴∠BCE=∠ACE﹣∠ACB=67.5°﹣45°=22.5°.
故答案为:22.5°.
17.(4分)如图,在?ABCD中,AB=3,BC=5,对角线AC、BD相交于点O,过点O作OE⊥AC,交AD于点E,连接CE,则△CDE的周长为 8 .
解:根据平行四边形的性质,
∴AO=OC,
∵OE⊥AC,
∴OE为AC的垂直平分线,
∴AE=EC,
∴△CDE的周长为:CD+AD=5+3=8,
故答案为:8.
18.(4分)如图的平面直角坐标系中,已知点A(﹣3,0)、B(0,4),将△OAB沿x轴作连续无滑动的翻滚,依次得到三角形①,②,③,④..则第?个三角形的直角顶点的坐标是 (60,0) .
解:∵点B(﹣3,0),A(0,4),
∴OB=3,OA=4,
∴AB==5,
∵对△OAB连续作如图所示的旋转变换,
∴△OAB每三次旋转后回到原来的状态,并且每三次向前移动了3+4+5=12个单位,
而7=3×2+1,
∴第⑦个三角形和第①个三角形的状态一样,则三角形⑦与三角形⑥的直角顶点相同,
∴三角形⑦的直角顶点的横坐标为2×12=24,纵坐标为0;
由题意可得:第16个三角形与第1个三角形状态相同,直角顶点的坐标为:(60,0),
故答案为(60,0).
三、解答题(本大题共8小题,共78分)
19.(8分)在边长为1的小正方形网格中,△AOB的顶点均在格点上,
(1)B点关于y轴的对称点坐标为 (﹣3,2) ;
(2)将△AOB向左平移4个单位长度得到△A1O1B1,请画出△A1O1B1.
解:(1)由图可知:
点B的坐标是(3,2)
所以B点关于y轴的对称点坐标为(﹣3,2);
故答案为:(﹣3,2);
(2)如图,△A1O1B1即为所求.
20.(8分)如图,四边形ABCD中,AD∥BC,对角线AC,BD交于点O,且OA=OC,求证:四边形ABCD是平行四边形.
【解答】证明:∵AD∥BC,
∴∠OAD=∠OCB,∠ADO=∠BCO.
又OA=OC,
∴△AOD≌△BOC.
∴OA=OC,OB=OD.
∴四边形ABCD为平行四边形.
21.(8分)游艇在湖面上以12千米/小时的速度向正东方向航行,在O处看到灯塔A在游艇北偏东60°方向上,航行1小时到达B处,此时看到灯塔A在游艇北偏西30°方向上,求此时游艇与灯塔的距离AB.
解:过点A作AC⊥OB交OB于C,则AC为所求,设AC=x,
由题意得:OB=12千米,∠AOC=30°,∠ABC=60°,
在Rt△ACO和Rt△ACB中:
tan30°=,tan60°=,
则OC=x,BC=x,
而OC+CB=x+x=12,
解得:x=3.
故AB===6(千米),
答:此时游艇与灯塔的距离AB为6千米.
22.(8分)如图,在平行四边形ABCD中,点P是对角线AC上的一点,PE⊥AB,PF⊥AD,垂足分别为E、F,且PE=PF,平行四边形ABCD是菱形吗?为什么?
解:是菱形.
理由如下:∵PE⊥AB,PF⊥AD,且PE=PF,
∴AC是∠DAB的角平分线,
∴∠DAC=∠CAE,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠DCA=∠CAB,
∴∠DAC=∠DCA,
∴DA=DC,
∴平行四边形ABCD是菱形.
23.(10分)如图,在?ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°.求∠B的度数.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠D=∠ECF,
在△ADE和△FCE中,,
∴△ADE≌△FCE(ASA);
(2)解:∵△ADE≌△FCE,
∴AD=FC,
∵AD=BC,AB=2BC,
∴AB=FB,
∴∠BAF=∠F=36°,
∴∠B=180°﹣2×36°=108°.
24.(10分)在?ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD.
∵BE∥DF,BE=DF,
∴四边形BFDE是平行四边形.
∵DE⊥AB,
∴∠DEB=90°,
∴四边形BFDE是矩形;
(2)∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠DFA=∠FAB.
在Rt△BCF中,由勾股定理,得
BC==5,
∴AD=BC=DF=5,
∴∠DAF=∠DFA,
∴∠DAF=∠FAB,
即AF平分∠DAB.
25.(13分)如图所示,在四边形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C出发沿着CB方向向点B以3cm/s的速度运动.点P,Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.
(1)经过多长时间,四边形PQCD是平行四边形?
(2)经过多长时间,四边形PQBA是矩形?
(3)若AB=8,如果Q点的移动速度不变,要使PQBA是正方形,则P点移动速度是多少?
解:(1)当PD=CQ时,四边形PQCD是平行四边形,设运动时间为ts.
∴24﹣t=3t,
解得t=6.
∴6s时,四边形PQCD是平行四边形.
(2)当AP=BQ时,四边形PQBA是矩形,设运动时间为ts.
∴t=26﹣3t,
解得t=,
∴s时,四边形PQBA是矩形.
(3)设运动时间为ts.当BQ=AB=8时,26﹣3t=8,
∴t=6,
∵PA=6?VP=8,
∴VP=cm/s.
26.(13分)如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
【解答】(1)证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
(2)解:四边形BECD是菱形,
理由是:∵D为AB中点,
∴AD=BD,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=BD(直角三角形斜边上的中线等于斜边的一半),
∴四边形BECD是菱形;
(3)当∠A=45°时,四边形BECD是正方形,理由是:
解:∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°,
∴AC=BC,
∵D为BA中点,
∴CD⊥AB,
∴∠CDB=90°,
∵四边形BECD是菱形,
∴菱形BECD是正方形,
即当∠A=45°时,四边形BECD是正方形.
同课章节目录
