2.2 等式与不等式性质,基本不等式习题课 课件(39张PPT)
文档属性
| 名称 | 2.2 等式与不等式性质,基本不等式习题课 课件(39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 573.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-03 22:44:13 | ||
图片预览








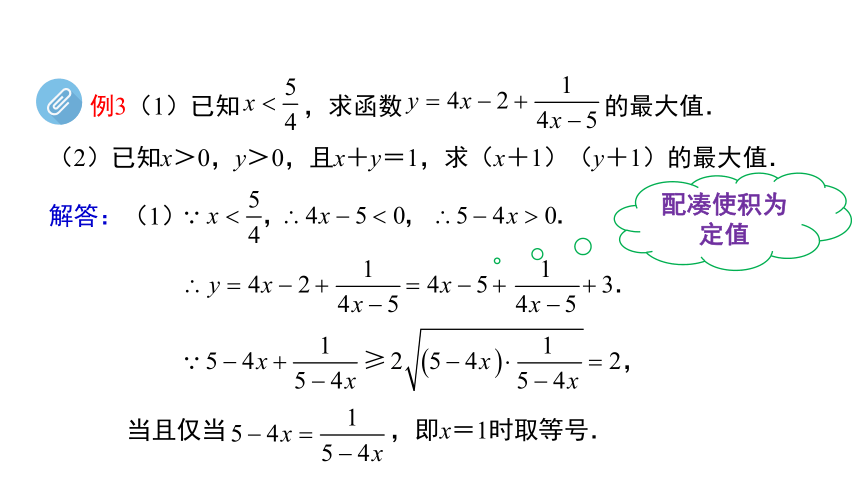


文档简介
等式与不等式性质、基本不等式习题课
复习回顾
不等式性质及注意事项
问题1 前面我们学习了不等式的基本性质和基本不等式,不等式有哪些性质?基本不等式能解决哪些问题?使用时需注意哪些条件?
基本不等式可以证明不等式或解决最值问题:
复习回顾
(1)如果正数x,y的积xy等于定值P,那么当且仅当x=y时,和x+y有最小值;
(2)如果正数x,y的和x+y等于定值S,那么当且仅当x=y时,积xy有最大值.
用基本不等式求最值时要注意满足三个条件:一正、二定、三相等.
典例研究
A. B. C. D.
(2)已知x∈R,下列说法中正确的是( )
A. 的最小值是2 B. , 的最小值是2
C. D.函数 的最小值2
D
C
例1 (1)若a>b>0,c<d<0,则一定有( )
问题2 每个题对应的知识点和方法分别是什么?
36
例1 (3)已知函数 在x=3时取得最小值,则a=________.
问题3 如何求上式的范围?用到哪些不等式性质?
解答:∵1<a<4,2<b<8,
∴2<2a<8,6<3b<24,
∴8<2a+3b<32.
典例研究
例2 已知1<a<4,2<b<8,求2a+3b的取值范围.
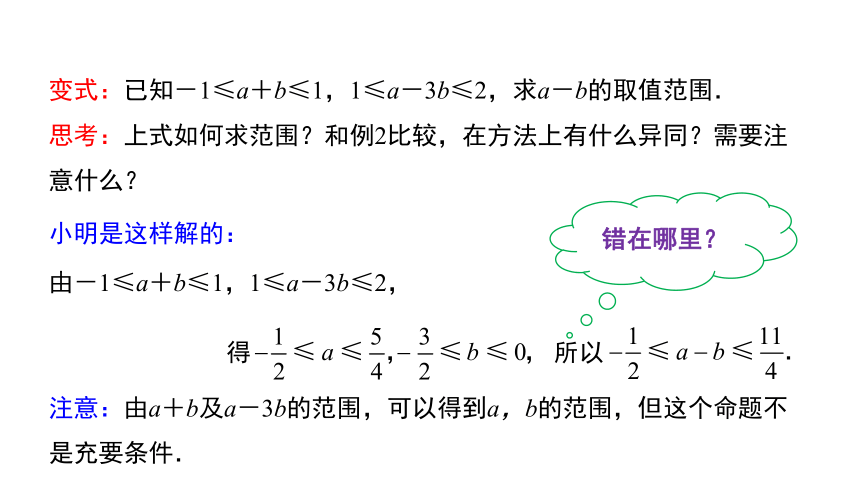
变式:已知-1≤a+b≤1,1≤a-3b≤2,求a-b的取值范围.
思考:上式如何求范围?和例2比较,在方法上有什么异同?需要注意什么?
小明是这样解的:
由-1≤a+b≤1,1≤a-3b≤2,
得
所以
错在哪里?
注意:由a+b及a-3b的范围,可以得到a,b的范围,但这个命题不是充要条件.
典例研究
变式:已知-1≤a+b≤1,1≤a-3b≤2,求a-b的取值范围.
思考:上式如何求范围?和例2比较,在方法上有什么异同?需要注意什么?
解答:设a-b=m(a+b)+n(a-3b)=(m+n)a+(m-3n)b,
解得
所以
则
由以上两式相加,得 .
典例研究
变式:已知-1≤a+b≤1,1≤a-3b≤2,求a-b的取值范围.
思考:上式如何求范围?和例2比较,在方法上有什么异同?需要注意什么?
总结:
利用几个不等式的范围来确定某个不等式的范围要注意:同向(异向)不等式的两边可以相加(相减),但是这种转化不是等价转化,如果在解题中多次使用,就有可能扩大取值范围.
典例研究
(2)已知x>0,y>0,且x+y=1,求(x+1)(y+1)的最大值.
解答:(1)
当且仅当 ,即x=1时取等号.
配凑使积为定值
典例研究
例3(1)已知 ,求函数 的最大值.
解答:(1)
即
故当x=1时,y取最大值1.
典例研究
(2)已知x>0,y>0,且x+y=1,求(x+1)(y+1)的最大值.
例3(1)已知 ,求函数 的最大值.
解答:(2)法1:由x+y=1,得y=1-x,
且0<x<1,则
当且仅当x+1=2-x ,即x=y= 时等号成立,
即 的最大值为 .
典例研究
(2)已知x>0,y>0,且x+y=1,求(x+1)(y+1)的最大值.
例3(1)已知 ,求函数 的最大值.
解答:(2)法2:由x+y=1,得y=1-x,
且0<x<1,则
即 的最大值为 .
当且仅当 ,即x=y= 时等号成立,
使得和为定值
典例研究
(2)已知x>0,y>0,且x+y=1,求(x+1)(y+1)的最大值.
例3(1)已知 ,求函数 的最大值.
则
即 的最大值为 .
当且仅当 ,即x=y= 时等号成立,
典例研究
(2)已知x>0,y>0,且x+y=1,求(x+1)(y+1)的最大值.
例3(1)已知 ,求函数 的最大值.
解答:(2)法3:∵x+y=1,∴
变式1:已知x>0,y>0,且 ,求x+y的最小值.
追问1 上面变式和例3比较,在解题思路上什么相同之处,你还有什么发现?
小丽是这样解的:
由 ,及 ,得xy≥36,
当且仅当 即x=2,y=18时取等号,
所以 , 取得最小值12.
错在哪里?
典例研究
变式1:已知x>0,y>0,且 ,求x+y的最小值.
且x>1,则
当且仅当 ,即x=4时取等号,
∴ 时, 取得最小值16.
减元,使得和为定值
典例研究
解答:法1:由 得 ,
变式1:已知x>0,y>0,且 ,求x+y的最小值.
∴
∴ 时, 取得最小值16.
∵x>0,y>0时,∴
则x+y ≥16,
当且仅当 ,又 ,
1的代换,把代数式构造成倒数形式,使得积为常数
典例研究
解答:法2:∵ ,
变式2:已知 ,且 ,求 的最小值.
∴
当且仅当 时取等号,
又 ,∴ , 取得最小值8.
典例研究
解答:∵ ,
变式3:已知 , ,求 的最小值.
所以所求式子的最小值为2.
则
当且仅当 ,即 时取等号,
典例研究
解答:由 ,得
*变式4:已知 x>0,y>0,且 x+3y=5xy,求3x+4y的最小值.
解答:法1:由 ,可得 .
∴ ,∴ 的最小值是5 .
当且仅当 时取等号,又 ,
典例研究
∴
*变式4:已知 x>0,y>0,且 x+3y=5xy,求3x+4y的最小值.
解答:法2:由 ,可得 ,
∴ 的最小值是5 .
当且仅当 时取等号,即
典例研究
∴
*变式4:已知 x>0,y>0,且 x+3y=5xy,求3x+4y的最小值.
解答:法3:由 ,可得 ,
典例研究
即
∴
∴ 的最小值是5 .
当且仅当 时取等号,即 等号成立,
解析:设一年的总费用为y万元,
故一年的总运费与总存储费用之和最小时x的值是30.
由题知 ,而
当且仅当 ,即 吨时取等号.
30
典例研究
例4 某公司一年购买某种货物600吨,每次都购买x吨,运费为6万元/次,一年的总存储费用为4x万元,要使一年的总运费与总存储费用之和最小,则 x=________吨.
归纳小结
(1)如何利用作差(商)法比较两个实数的大小?
作差法步骤:作差、变形、定号、定论,适合所有的数或式
作商法步骤:作商、变形、定号、定论,适合同号的数或式
问题6 回顾本节学习过程,回答以下问题:
归纳小结
问题6 回顾本节学习过程,回答以下问题:
(2)不等式的基本性质有哪些?需要注意哪些条件?
基本不等式是:
归纳小结
可以证明不等式或解决以下最值问题:
(1)如果正数x,y的积xy等于定值P,那么当且仅当x=y时,和x+y有最小值;(2)如果正数x,y的和x+y等于定值S,那么当且仅当x=y时,积xy有最大值.
问题6 回顾本节学习过程,回答以下问题:
(3)基本不等式是什么?能够解决什么问题?在解决问题时应注意什么?
归纳小结
会将问题中的条件进行变形或转化,使其满足基本不等式的条件.
用基本不等式求最值时要注意满足三个条件:一正、二定、三相等.
问题6 回顾本节学习过程,回答以下问题:
(3)基本不等式是什么?能够解决什么问题?在解决问题时应注意什么?
作业:教科书复习参考题2第1,2,3,4题.
作业布置
目标检测
A.c-a<c-b B.
C. D.
A
取a=1,b=-1,B,C选项都错了.
对于D,取a=-1,b=-2,D也错了.
由不等式的性质4可乘性知-a<-b,
再根据可加性得c-a<c-b选项正确,故选A.
设a,b,c∈R,且a>b,则下列不等式成立的是( )
1
分析:利用不等式的性质或者举反例判断.
目标检测
A. 2 B. C. 4 D. 5
C
即a=b时,取“=”号.
当且仅当 ,
且 ,
分析:因为
已知a>0,b>0,则 的最小值是( )
2
目标检测
(2)若0<x<1,则 的最小值为_______.
8
9
(1)若a>0,b>0,ab=2a+b,则a+b的最小值为________,ab的最小值为_______.
3
目标检测
∵x2+6>0,
∴当 时, ,即 ;
当x=1时, ,即 ;
当x<1时, ,即 .
已知x∈R,试比较x3+6x与x2+6的大小.
4
解:
目标检测
当且仅当 时取等号,
又
的最大值是 .
设a>0,b>0,a2+ =1求 的最大值.
5
解:
目标检测
∴
以上三个不等式相加,得
即
已知a,b,c为不全相等的正实数,且abc=1.
求证: .
6
证明:∵a,b,c都是正实数,且abc=1,
目标检测
所以上述三个等式中的“=”不都同时成立,
所以
已知a,b,c为不全相等的正实数,且abc=1.
求证: .
6
证明:∵a,b,c不全相等,
目标检测
某农场有一废弃的猪圈,留有一面旧墙长12 m,现准备在该地区重新建一个猪圈.平面图为矩形,面积为56 m2,预计:①修复1 m旧墙的费用是建造1 m新墙费用的25%,②拆去1 m旧墙所得材料用以建成1 m新墙的费用是建1 m新墙费用的50%,③为安装圈门,要在围墙的适当处留出1 m的空缺.试问:这里建造猪圈的围墙应当怎样利用旧墙,才能使所需的总费用最小?
7
目标检测
解:显然,使旧墙全部得到利用,并把圈门留在新墙处为好.
则剩下的旧墙拆得的材料可建造新墙(12-x)m,
于是还需建造新墙的长为
设修复成新墙的旧墙为x m,
目标检测
解:设建造1 m新墙所需a元,建造围墙的总费用为y元,
又x>0, ∴ ,
当且仅当 ,即x=8时,上式等号成立.
因此修复的旧墙约为8 m,拆除并改建成新墙的旧墙约为4 m时,
建造的总费用最小.
再见
复习回顾
不等式性质及注意事项
问题1 前面我们学习了不等式的基本性质和基本不等式,不等式有哪些性质?基本不等式能解决哪些问题?使用时需注意哪些条件?
基本不等式可以证明不等式或解决最值问题:
复习回顾
(1)如果正数x,y的积xy等于定值P,那么当且仅当x=y时,和x+y有最小值;
(2)如果正数x,y的和x+y等于定值S,那么当且仅当x=y时,积xy有最大值.
用基本不等式求最值时要注意满足三个条件:一正、二定、三相等.
典例研究
A. B. C. D.
(2)已知x∈R,下列说法中正确的是( )
A. 的最小值是2 B. , 的最小值是2
C. D.函数 的最小值2
D
C
例1 (1)若a>b>0,c<d<0,则一定有( )
问题2 每个题对应的知识点和方法分别是什么?
36
例1 (3)已知函数 在x=3时取得最小值,则a=________.
问题3 如何求上式的范围?用到哪些不等式性质?
解答:∵1<a<4,2<b<8,
∴2<2a<8,6<3b<24,
∴8<2a+3b<32.
典例研究
例2 已知1<a<4,2<b<8,求2a+3b的取值范围.
变式:已知-1≤a+b≤1,1≤a-3b≤2,求a-b的取值范围.
思考:上式如何求范围?和例2比较,在方法上有什么异同?需要注意什么?
小明是这样解的:
由-1≤a+b≤1,1≤a-3b≤2,
得
所以
错在哪里?
注意:由a+b及a-3b的范围,可以得到a,b的范围,但这个命题不是充要条件.
典例研究
变式:已知-1≤a+b≤1,1≤a-3b≤2,求a-b的取值范围.
思考:上式如何求范围?和例2比较,在方法上有什么异同?需要注意什么?
解答:设a-b=m(a+b)+n(a-3b)=(m+n)a+(m-3n)b,
解得
所以
则
由以上两式相加,得 .
典例研究
变式:已知-1≤a+b≤1,1≤a-3b≤2,求a-b的取值范围.
思考:上式如何求范围?和例2比较,在方法上有什么异同?需要注意什么?
总结:
利用几个不等式的范围来确定某个不等式的范围要注意:同向(异向)不等式的两边可以相加(相减),但是这种转化不是等价转化,如果在解题中多次使用,就有可能扩大取值范围.
典例研究
(2)已知x>0,y>0,且x+y=1,求(x+1)(y+1)的最大值.
解答:(1)
当且仅当 ,即x=1时取等号.
配凑使积为定值
典例研究
例3(1)已知 ,求函数 的最大值.
解答:(1)
即
故当x=1时,y取最大值1.
典例研究
(2)已知x>0,y>0,且x+y=1,求(x+1)(y+1)的最大值.
例3(1)已知 ,求函数 的最大值.
解答:(2)法1:由x+y=1,得y=1-x,
且0<x<1,则
当且仅当x+1=2-x ,即x=y= 时等号成立,
即 的最大值为 .
典例研究
(2)已知x>0,y>0,且x+y=1,求(x+1)(y+1)的最大值.
例3(1)已知 ,求函数 的最大值.
解答:(2)法2:由x+y=1,得y=1-x,
且0<x<1,则
即 的最大值为 .
当且仅当 ,即x=y= 时等号成立,
使得和为定值
典例研究
(2)已知x>0,y>0,且x+y=1,求(x+1)(y+1)的最大值.
例3(1)已知 ,求函数 的最大值.
则
即 的最大值为 .
当且仅当 ,即x=y= 时等号成立,
典例研究
(2)已知x>0,y>0,且x+y=1,求(x+1)(y+1)的最大值.
例3(1)已知 ,求函数 的最大值.
解答:(2)法3:∵x+y=1,∴
变式1:已知x>0,y>0,且 ,求x+y的最小值.
追问1 上面变式和例3比较,在解题思路上什么相同之处,你还有什么发现?
小丽是这样解的:
由 ,及 ,得xy≥36,
当且仅当 即x=2,y=18时取等号,
所以 , 取得最小值12.
错在哪里?
典例研究
变式1:已知x>0,y>0,且 ,求x+y的最小值.
且x>1,则
当且仅当 ,即x=4时取等号,
∴ 时, 取得最小值16.
减元,使得和为定值
典例研究
解答:法1:由 得 ,
变式1:已知x>0,y>0,且 ,求x+y的最小值.
∴
∴ 时, 取得最小值16.
∵x>0,y>0时,∴
则x+y ≥16,
当且仅当 ,又 ,
1的代换,把代数式构造成倒数形式,使得积为常数
典例研究
解答:法2:∵ ,
变式2:已知 ,且 ,求 的最小值.
∴
当且仅当 时取等号,
又 ,∴ , 取得最小值8.
典例研究
解答:∵ ,
变式3:已知 , ,求 的最小值.
所以所求式子的最小值为2.
则
当且仅当 ,即 时取等号,
典例研究
解答:由 ,得
*变式4:已知 x>0,y>0,且 x+3y=5xy,求3x+4y的最小值.
解答:法1:由 ,可得 .
∴ ,∴ 的最小值是5 .
当且仅当 时取等号,又 ,
典例研究
∴
*变式4:已知 x>0,y>0,且 x+3y=5xy,求3x+4y的最小值.
解答:法2:由 ,可得 ,
∴ 的最小值是5 .
当且仅当 时取等号,即
典例研究
∴
*变式4:已知 x>0,y>0,且 x+3y=5xy,求3x+4y的最小值.
解答:法3:由 ,可得 ,
典例研究
即
∴
∴ 的最小值是5 .
当且仅当 时取等号,即 等号成立,
解析:设一年的总费用为y万元,
故一年的总运费与总存储费用之和最小时x的值是30.
由题知 ,而
当且仅当 ,即 吨时取等号.
30
典例研究
例4 某公司一年购买某种货物600吨,每次都购买x吨,运费为6万元/次,一年的总存储费用为4x万元,要使一年的总运费与总存储费用之和最小,则 x=________吨.
归纳小结
(1)如何利用作差(商)法比较两个实数的大小?
作差法步骤:作差、变形、定号、定论,适合所有的数或式
作商法步骤:作商、变形、定号、定论,适合同号的数或式
问题6 回顾本节学习过程,回答以下问题:
归纳小结
问题6 回顾本节学习过程,回答以下问题:
(2)不等式的基本性质有哪些?需要注意哪些条件?
基本不等式是:
归纳小结
可以证明不等式或解决以下最值问题:
(1)如果正数x,y的积xy等于定值P,那么当且仅当x=y时,和x+y有最小值;(2)如果正数x,y的和x+y等于定值S,那么当且仅当x=y时,积xy有最大值.
问题6 回顾本节学习过程,回答以下问题:
(3)基本不等式是什么?能够解决什么问题?在解决问题时应注意什么?
归纳小结
会将问题中的条件进行变形或转化,使其满足基本不等式的条件.
用基本不等式求最值时要注意满足三个条件:一正、二定、三相等.
问题6 回顾本节学习过程,回答以下问题:
(3)基本不等式是什么?能够解决什么问题?在解决问题时应注意什么?
作业:教科书复习参考题2第1,2,3,4题.
作业布置
目标检测
A.c-a<c-b B.
C. D.
A
取a=1,b=-1,B,C选项都错了.
对于D,取a=-1,b=-2,D也错了.
由不等式的性质4可乘性知-a<-b,
再根据可加性得c-a<c-b选项正确,故选A.
设a,b,c∈R,且a>b,则下列不等式成立的是( )
1
分析:利用不等式的性质或者举反例判断.
目标检测
A. 2 B. C. 4 D. 5
C
即a=b时,取“=”号.
当且仅当 ,
且 ,
分析:因为
已知a>0,b>0,则 的最小值是( )
2
目标检测
(2)若0<x<1,则 的最小值为_______.
8
9
(1)若a>0,b>0,ab=2a+b,则a+b的最小值为________,ab的最小值为_______.
3
目标检测
∵x2+6>0,
∴当 时, ,即 ;
当x=1时, ,即 ;
当x<1时, ,即 .
已知x∈R,试比较x3+6x与x2+6的大小.
4
解:
目标检测
当且仅当 时取等号,
又
的最大值是 .
设a>0,b>0,a2+ =1求 的最大值.
5
解:
目标检测
∴
以上三个不等式相加,得
即
已知a,b,c为不全相等的正实数,且abc=1.
求证: .
6
证明:∵a,b,c都是正实数,且abc=1,
目标检测
所以上述三个等式中的“=”不都同时成立,
所以
已知a,b,c为不全相等的正实数,且abc=1.
求证: .
6
证明:∵a,b,c不全相等,
目标检测
某农场有一废弃的猪圈,留有一面旧墙长12 m,现准备在该地区重新建一个猪圈.平面图为矩形,面积为56 m2,预计:①修复1 m旧墙的费用是建造1 m新墙费用的25%,②拆去1 m旧墙所得材料用以建成1 m新墙的费用是建1 m新墙费用的50%,③为安装圈门,要在围墙的适当处留出1 m的空缺.试问:这里建造猪圈的围墙应当怎样利用旧墙,才能使所需的总费用最小?
7
目标检测
解:显然,使旧墙全部得到利用,并把圈门留在新墙处为好.
则剩下的旧墙拆得的材料可建造新墙(12-x)m,
于是还需建造新墙的长为
设修复成新墙的旧墙为x m,
目标检测
解:设建造1 m新墙所需a元,建造围墙的总费用为y元,
又x>0, ∴ ,
当且仅当 ,即x=8时,上式等号成立.
因此修复的旧墙约为8 m,拆除并改建成新墙的旧墙约为4 m时,
建造的总费用最小.
再见
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
